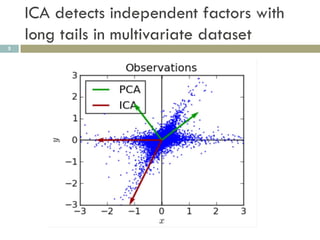
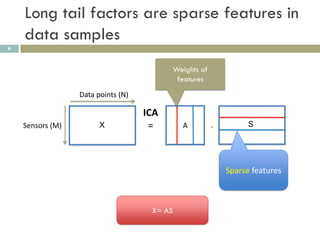
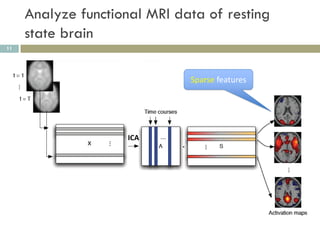
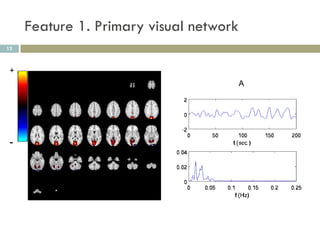
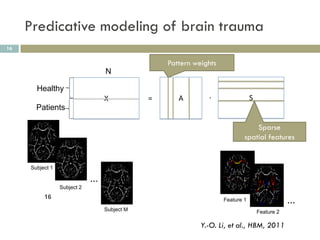
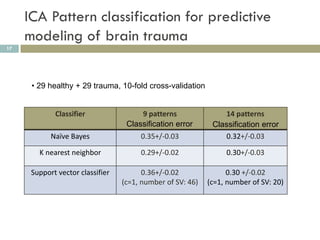
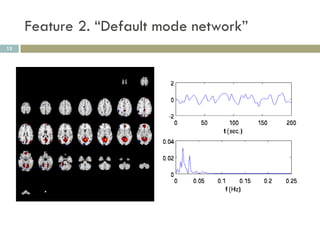
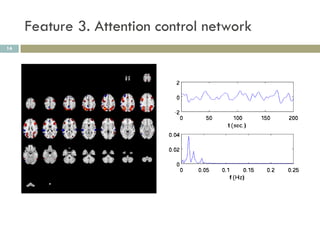
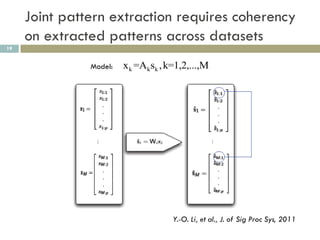
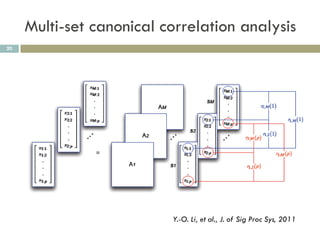
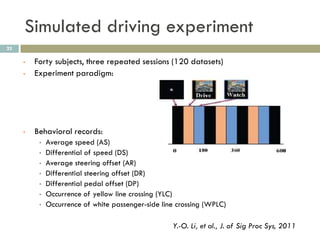
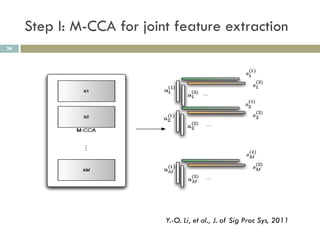
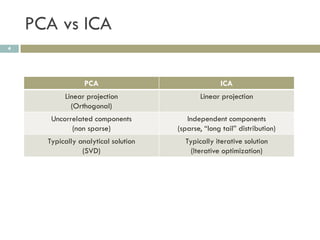
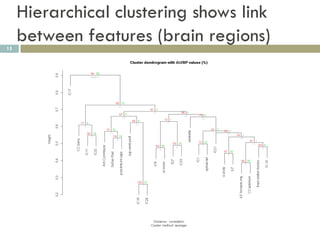
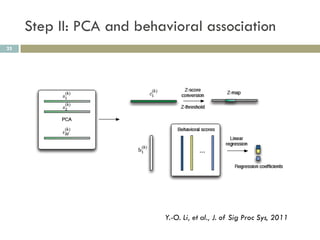
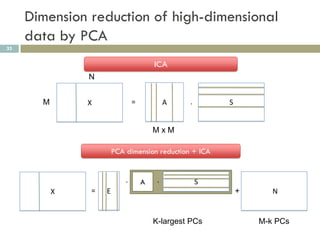
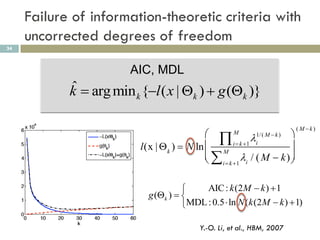
1) ICA can extract sparse and independent features from medical imaging data to build predictive models of conditions like brain trauma. 2) MCCA identifies joint patterns across multiple datasets, like functional MRI scans from a simulated driving experiment. 3) Dimension reduction with PCA improves ICA by addressing issues with high dimensionality, enhancing reproducibility of extracted patterns.

1. 1
MACHINE LEARNING FOR
MEDICAL IMAGING DATA
Yiou (Leo) Li

2. Background
2
Post-doctoral fellow, 07/2009-Present, Neural connectivity Laboratory,
University of California San Francisco
• Developed unsupervised learning method for feature extraction of brain
imaging data
• Applied supervised learning (Naïve Bayes, SVM, Random Forest) for predictive
modeling of brain trauma
• Designed batch data processing protocol to perform image registration,
segmentation, band-pass filtering, smoothing, and linear model fitting
Graduate Research Assistant, 08/2002-06/2009, Machine learning for signal
processing Laboratory, University of Maryland Baltimore County
• Developed the effective degrees of freedom of random process and applied it
to the model order selection by Information Theoretic Criteria
• Developed a linear filtering mechanism in independent component analysis for
feature enhancement
• Analyzed canonical correlation analysis for multiple datasets

3. Outline
3
 Independent component analysis (ICA) and its
application to sparse feature extraction from
multivariate dataset
 Multi-set canonical correlation analysis and its
application to joint pattern extraction from a group of
datasets
 Order selection of principal component analysis (PCA)
and its application to data dimension reduction

4. PCA vs ICA
4
PCA ICA
Linear projection Linear projection
(Orthogonal)
Uncorrelated components Independent components
(non sparse) (sparse, “long tail” distribution)
Typically analytical solution Typically iterative solution
(SVD) (Iterative optimization)

5. ICA detects independent factors with
long tails in multivariate dataset
5

6. Long tail factors are sparse features in
data samples
6
Weights of
features
Data points (N)
ICA
Sensors (M) X = A . S
Sparse features
X= AS

7. ICA model
7
 x1   a11 a12 ... a1M   s1 
x  a a 22 a 2M   s 2 
 2    21  
 ...   ...   ... 
     
 x M  a M1 a M2 a MM  s M 
x : Observed variables
A : Mixing matrix
s : Latent factors
x= As -> s =A-1x

8. ICA by maximum likelihood estimation
8
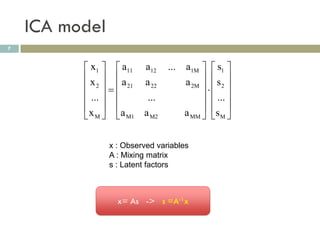
Transformation of multivariate random variable: x = As
p(s 1, s2 , ... , sM )
p(x 1,x 2 , ... , x M )  (1)
det(A)
Statistical independence condition of s:
p(s 1, s2 , ... , sM )  i 1 p(si )
M
(2)
Log likelihood function of x with parameter A:
log p(x 1,x 2 ,...x M )   log p([A x] i )  log det(A)
-1
i

9. ICA Application: Sparse feature extraction from
multivariate dataset
9

10. Functional MRI experiment
10

11. Analyze functional MRI data of resting
state brain
11
Sparse features
ICA

12. Feature 1. Primary visual network
12
+
A
-

13. Feature 2. “Default mode network”
13

14. Feature 3. Attention control network
14

15. Hierarchical clustering shows link
15
between features (brain regions)

16. Predicative modeling of brain trauma
16
Pattern weights
N
Healthy
X = A . S
Patients
Sparse
spatial features
Subject 1
…
Subject 2
16 Pattern 2
Feature 1 …
Subject M Feature 2
Y.-O. Li, et al., HBM, 2011

17. ICA Pattern classification for predictive
modeling of brain trauma
17
• 29 healthy + 29 trauma, 10-fold cross-validation
Classifier 9 patterns 14 patterns
Classification error Classification error
Naïve Bayes 0.35+/-0.03 0.32+/-0.03
K nearest neighbor 0.29+/-0.02 0.30+/-0.03
Support vector classifier 0.36+/-0.02 0.30 +/-0.02
(c=1, number of SV: 46) (c=1, number of SV: 20)

18. Outline
18
 Independent component analysis (ICA) and its
application to sparse feature extraction from
multivariate dataset
 Multi-set canonical correlation analysis and its
application to joint pattern extraction from a group of
datasets
 Order selection of principal component analysis (PCA)
and its application to dimension reduction

19. Joint pattern extraction requires coherency
on extracted patterns across datasets
19
Model: x k =Aksk , k=1,2,...,M
Y.-O. Li, et al., J. of Sig Proc Sys, 2011

20. Multi-set canonical correlation analysis
20
Y.-O. Li, et al., J. of Sig Proc Sys, 2011

21. Multi-set canonical correlation
analysis
21
Correlation matrix of [S1,S2, … SM]
Y.-O. Li, et al., J. of Sig Proc Sys, 2011

22. Application: joint pattern extraction from a
group of datasets
22
• Analyze group functional MRI data from
simulated driving experiment

23. Simulated driving experiment
23
• Forty subjects, three repeated sessions (120 datasets)
• Experiment paradigm:
• Behavioral records:
• Average speed (AS)
• Differential of speed (DS)
• Average steering offset (AR)
• Differential steering offset (DR)
• Differential pedal offset (DP)
• Occurrence of yellow line crossing (YLC)
• Occurrence of white passenger-side line crossing (WPLC)
Y.-O. Li, et al., J. of Sig Proc Sys, 2011

24. Step I: M-CCA for joint feature extraction
24
Y.-O. Li, et al., J. of Sig Proc Sys, 2011

25. Step II: PCA and behavioral association
25
Y.-O. Li, et al., J. of Sig Proc Sys, 2011

26. Pattern 1: Primary visual function
26
D = 0:85
W = 0:42
95% CI of behavioral association

27. Pattern 2: “default mode network”
27
D = -0.63
W = -0.39
95% CI of behavioral association

28. Pattern 3: Motor coordination
28
D = 0.86
W = 0.15
95% CI of behavioral association

29. Pattern 4: Executive control network
29
D = 0.64
W = 0.61
95% CI of behavioral association

30. Cross correlation of Pattern 1
30
Y.-O. Li, et al., J. of Sig Proc Sys, 2011

31. Outline
31
 Independent component analysis (ICA) and its
application to sparse feature extraction from
multivariate dataset
 Multi-set canonical correlation analysis and its
application to joint pattern extraction from a group of
datasets
 Order selection of principal component analysis (PCA)
and its application to data dimension reduction

32. Decreased reproducibility of independent
component on high-dimensional dataset
32
• Functional MRI with 120 time points
• Twenty Monte Carlo trials of ICA algorithm
• Clustering the IC estimates
• Reproducible ICs: compact and separated clusters
K=20 K=40 K=90
Y.-O. Li, et al., HBM, 2007

33. Dimension reduction of high-dimensional
data by PCA
33
ICA N
N
M X = A . S
MxM
PCA dimension reduction + ICA
. A . S
X = E + N
K-largest PCs M-k PCs

34. Failure of information-theoretic criteria with
uncorrected degrees of freedom
34
AIC, MDL
ˆ
k  arg min k {l ( x | k )  g (k )}
( M k)
 
 i k 1 
M 1/ ( M  k )
l(x |  k )  N ln  M i


 i k 1 i / ( M  k) 

 AIC : k (2M  k )  1
g ( k )  
MDL : 0.5  ln N (k (2M  k )  1)
Y.-O. Li, et al., HBM, 2007

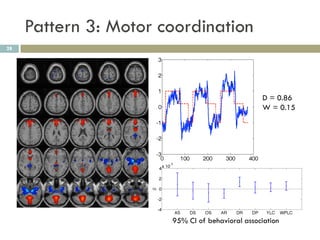
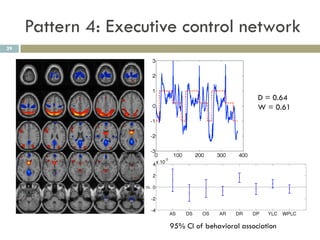
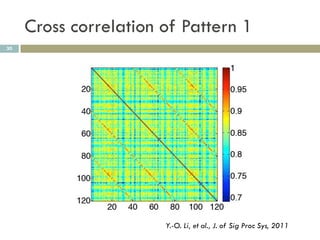
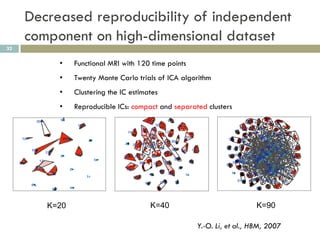
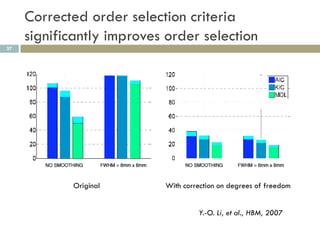
35. Estimation of degrees of freedom by
entropy rate
35
Entropy rate of a Gaussian process
1 
h( x)  ln 2 e 
4   ln s()d

h( x)  ln 2 e iff x[n] is an i.i.d. random process
h(x) = 0.40 h(x) = 1.28 h(x) = 1.41
Y.-O. Li, et al., HBM, 2007

36. Application: Order selection of high-
dimensional dataset
36

37. Corrected order selection criteria
significantly improves order selection
37
Original With correction on degrees of freedom
Y.-O. Li, et al., HBM, 2007

38. Summary
38
• ICA extracts useful patterns from high dimensional imaging data for
predictive modeling
• M-CCA reveals patterns from several datasets in a coherent order
• Dimension reduction by PCA improves the reproducibility of ICA extracted
patterns
Exploratory multivariate analysis are promising tools for
data mining applications