The document discusses condition monitoring of machinery using artificial intelligence techniques. It presents:
1) Condition monitoring and artificial intelligence can help automate monitoring of steady and unsteady equipment by analyzing variable parameters like loads, speeds and temperatures.
2) The theory of condition monitoring and artificial intelligence is explained, along with experimental work on methodology and results.
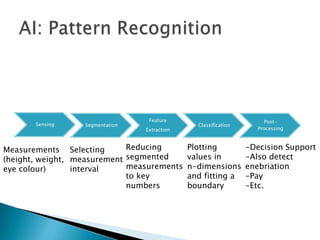
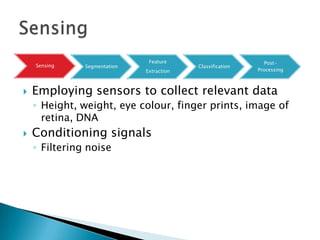
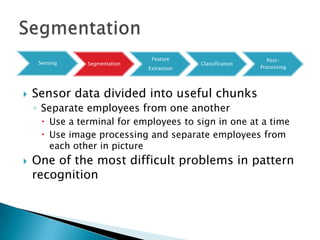
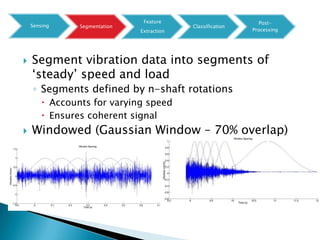
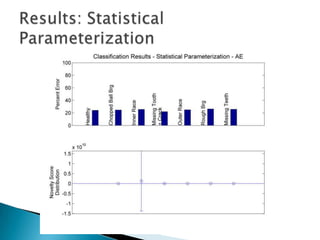
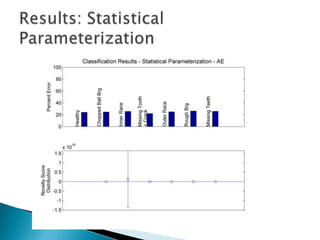
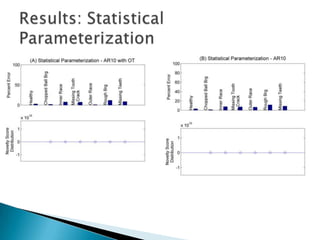
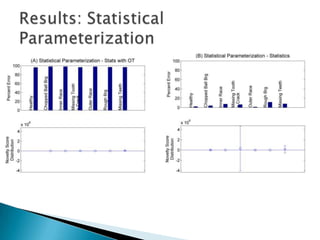
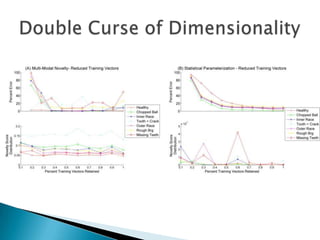
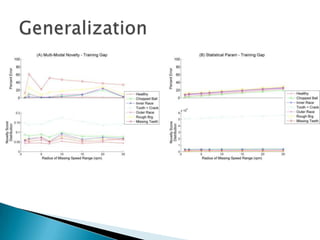
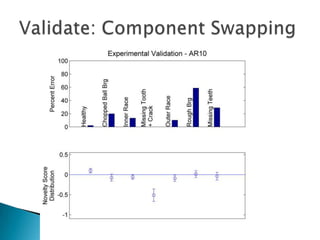
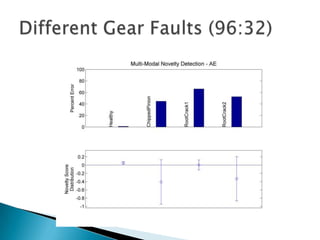
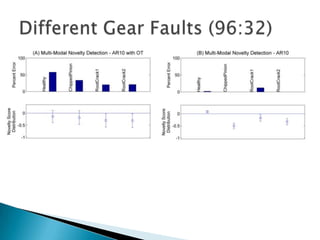
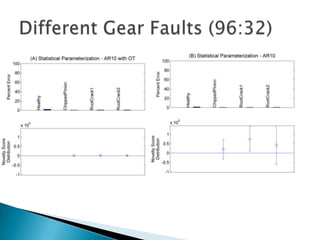
3) Monitoring multi-modal machinery requires techniques spanning sensing, segmentation, feature extraction, classification and post-processing to determine machinery health from noisy parameter data.