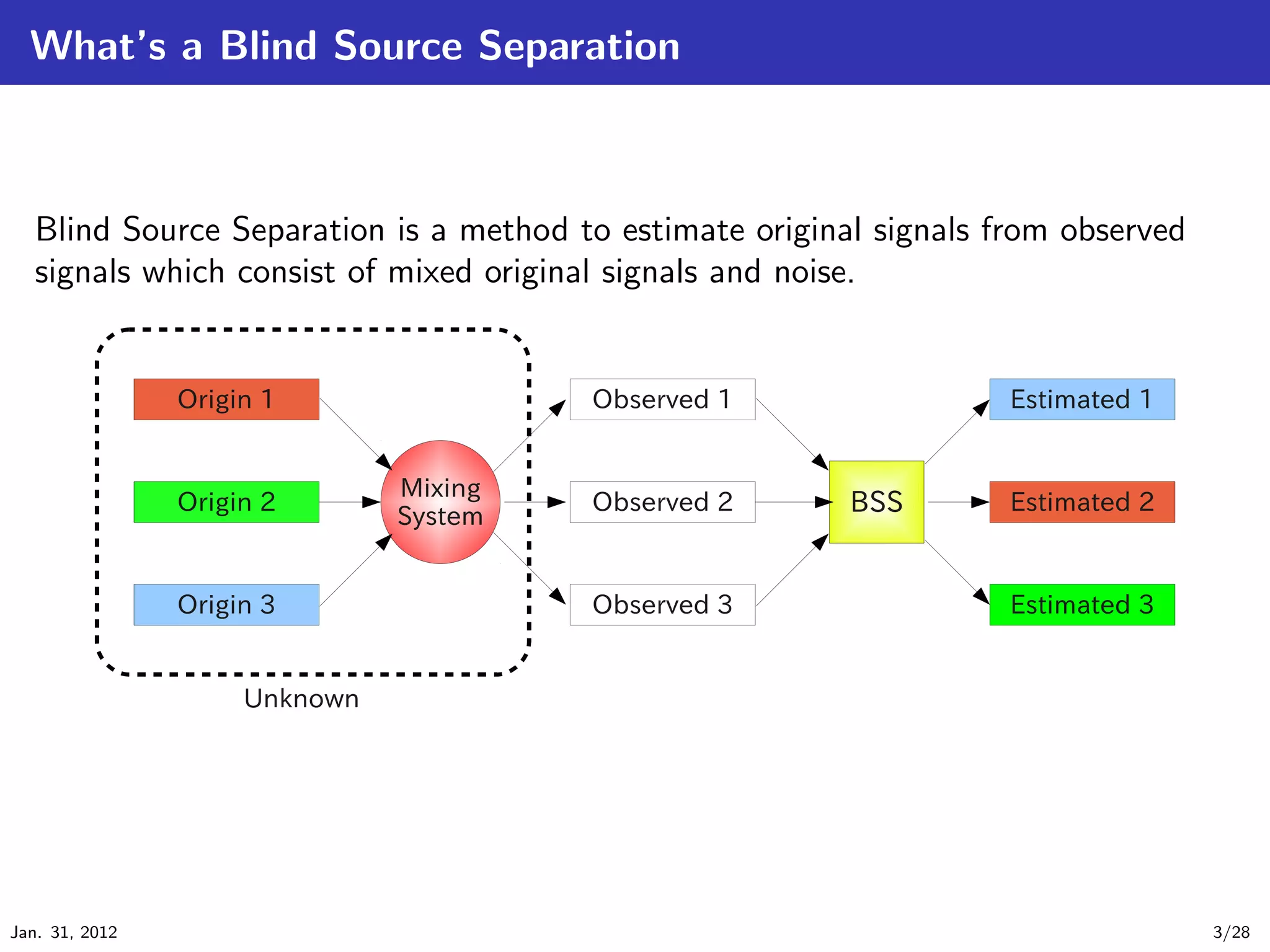
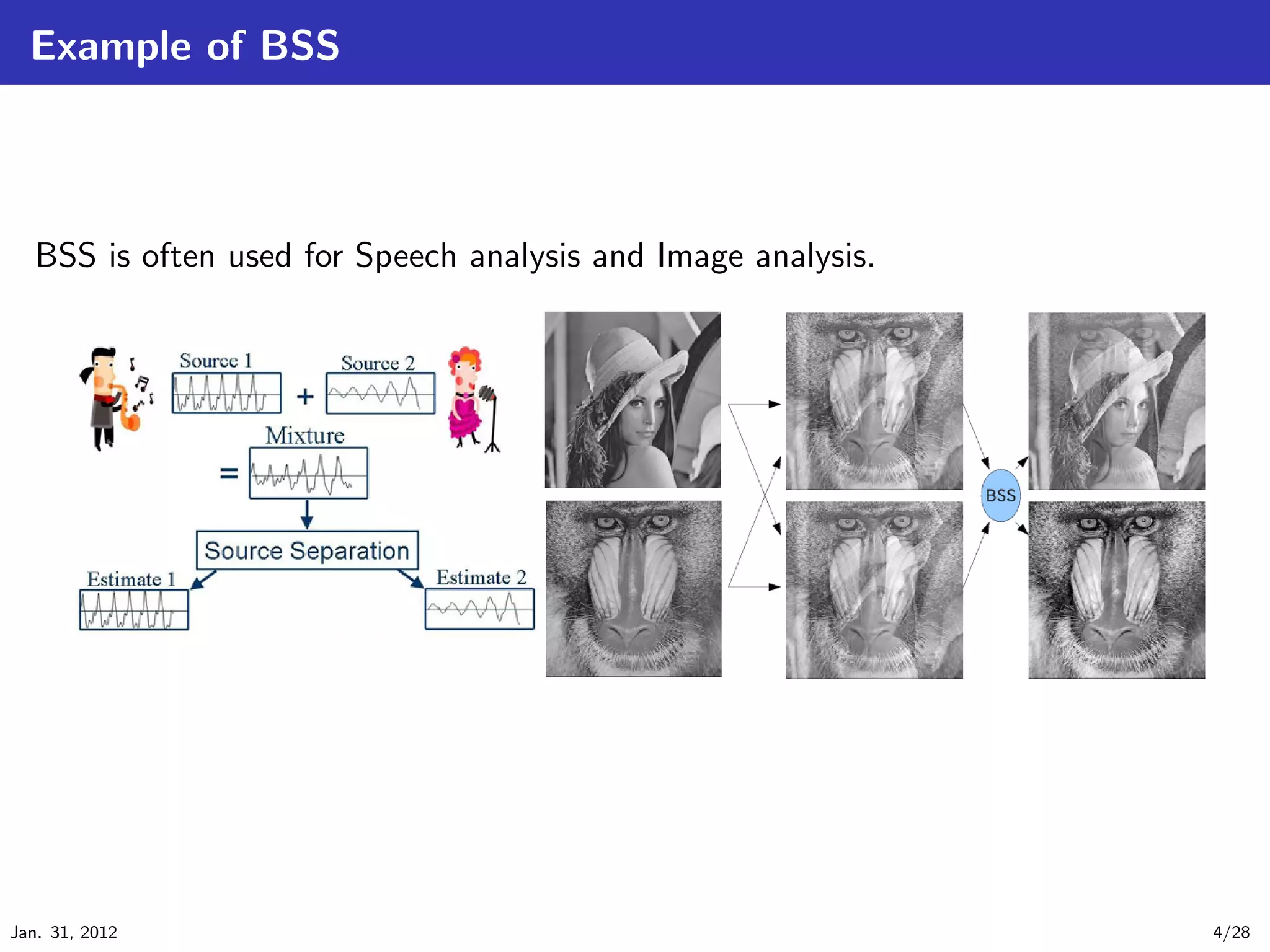
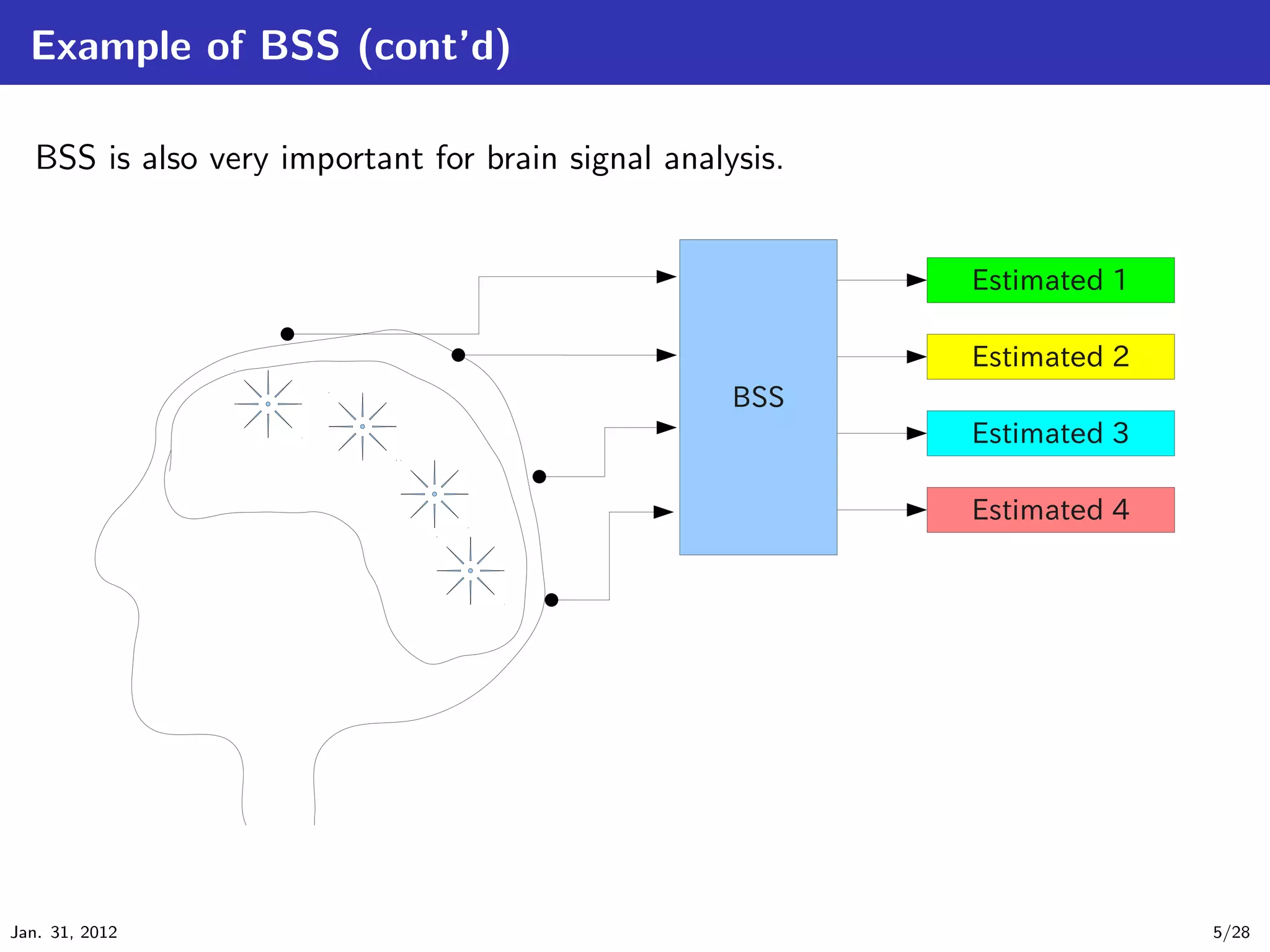
This document discusses independent component analysis (ICA) for blind source separation. ICA is a method to estimate original signals from observed signals consisting of mixed original signals and noise. It introduces the ICA model and approach, including whitening, maximizing non-Gaussianity using kurtosis and negentropy, and fast ICA algorithms. The document provides examples applying ICA to separate images and discusses approaches to improve ICA, including using differential filtering. ICA is an important technique for blind source separation and independent component estimation from observed signals.

1. .
.
Independent Component Analysis for Blind Source
Separation
.
.. .
.
Tatsuya Yokota
Tokyo Institute of Technology
Jan. 31, 2012
Jan. 31, 2012 1/28

2. Outline
.
. . Blind Source Separation
1
.
. . Independent Component Analysis
2
.
. . Experiments
3
.
. . Summary
4
Jan. 31, 2012 2/28

3. What’s a Blind Source Separation
Blind Source Separation is a method to estimate original signals from observed
signals which consist of mixed original signals and noise.
Jan. 31, 2012 3/28

4. Example of BSS
BSS is often used for Speech analysis and Image analysis.
Jan. 31, 2012 4/28

5. Example of BSS (cont’d)
BSS is also very important for brain signal analysis.
Jan. 31, 2012 5/28

6. Model Formalization
The problem of BSS is formalized as follow:
The matrix
X ∈ Rm×d (1)
denotes original signals, where m is number of original signals, and d is dimension
of one signal.
We consider that the observed signals Y ∈ Rn×d are given by linear mixing system
as
Y = AX + E, (2)
where A ∈ Rn×m is the unknown mixing matrix and E ∈ Rn×d denotes a noise.
Basically, n ≥ m.
ˆ ˆ ˆ
The goal of BSS is to estimate A and X so that X provides unknown original
signal as possible.
Jan. 31, 2012 6/28

7. Kinds of BSS Methods
Actually, degree of freedom of BSS model is very high to estimate A and X.
Because there are a huge number of combinations (A, X) which satisfy
Y = AX + E.
Therefore, we need some constraint to solve the BSS problem such as:
PCA : orthogonal constraint
SCA : sparsity constraint
NMF : non-negativity constraint
ICA : in-dependency constraint
In this way, there are many methods to solve the BSS problem depending on the
constraints. What we use is depend on subject matter.
The Non-negative Matrix Factorization(NMF) was introduced in my previous
seminar. We can get its solution by the alternating least squares algorithm.
Today, I will introduce another method the Independent Component Analysis.
Jan. 31, 2012 7/28

8. Independent Component Analysis
.
The Cocktail Party Problem .
..
x1 (t) = a11 s1 (t) + a12 s2 (t) + a13 s3 (t) (3)
x2 (t) = a21 s1 (t) + a22 s2 (t) + a23 s3 (t) (4)
. x3 (t) = a31 s1 (t) + a32 s2 (t) + a33 s3 (t) (5)
.. .
.
x is an observed signal, and s is an original signal. We assume that {s1 , s2 , s3 }
are statistically independent of each other.
.
The model of ICA .
..
Independent Component Analysis (ICA) is to estimate the independent
components s(t) from x(t).
. x(t) = As(t) (6)
.. .
.
Jan. 31, 2012 8/28

9. Approach
.
Hypothesis of ICA .
..
... {si } are statistically independent of each other,
1
p(s1 , s2 , . . . , sn ) = p(s1 )p(s2 ) · · · p(sn ). (7)
...
2 {si } follow the Non-Gaussian distribution.
If {si } follows the Gaussian distribution, then ICA is impossible.
... A is a regular matrix.
3
Therefore, we can rewrite the model as
s(t) = Bx(t), (8)
where B = A−1 . It is only necessary to estimate B so that {si } are
. independent.
.. .
.
Jan. 31, 2012 9/28

10. Whitening and ICA
.
Definition of White signal .
..
White signals are defined as any z which satisfies conditions of
. E[z] = 0, E[zz T ] = I. (9)
.. .
.
First, we show an example of original independent signals and observed signal as
follow:
(a) source (s1 , s2 ) (b) observed (x1 , x2 )
Observed signals x(t) are given by x(t) = As(t).
ICA give us the original signals s(t) by s(t) = Bx(t).
Jan. 31, 2012 10/28

11. Whitening and ICA (cont’d)
Whitening is useful for preprocessing of ICA.
First, we apply the whitening to observed signals x(t).
(c) observed (x1 , x2 ) (d) whitening (z1 , z2 )
The whitening signals are denoted as (z1 , z2 ), and they are given by
z(t) = V x(t), (10)
where V is a whitening matrix for x. Model becomes
s(t) = U z(t) = U V x(t) = Bx(t), (11)
and U is an orthogonal transform matrix. We can say that the whitening
simplifies the ICA problem. So it is only necessary to estimate U .
Jan. 31, 2012 11/28

12. Non-Gaussianity and ICA
Non-Gaussianity is a measure of in-dependency.
According to the central limit theorem, the Gaussianity of x(t) must be larger
than s(t).
Now, we put bT as mixing vector, si (t) = bT x(t). We want to maximize the
i ˆ i
Non-Gaussianity of (bT x(t)). Then such b is a part of solution B.
i
For example, there are following two vector b and b. We can say that b is better
than b .
Jan. 31, 2012 12/28

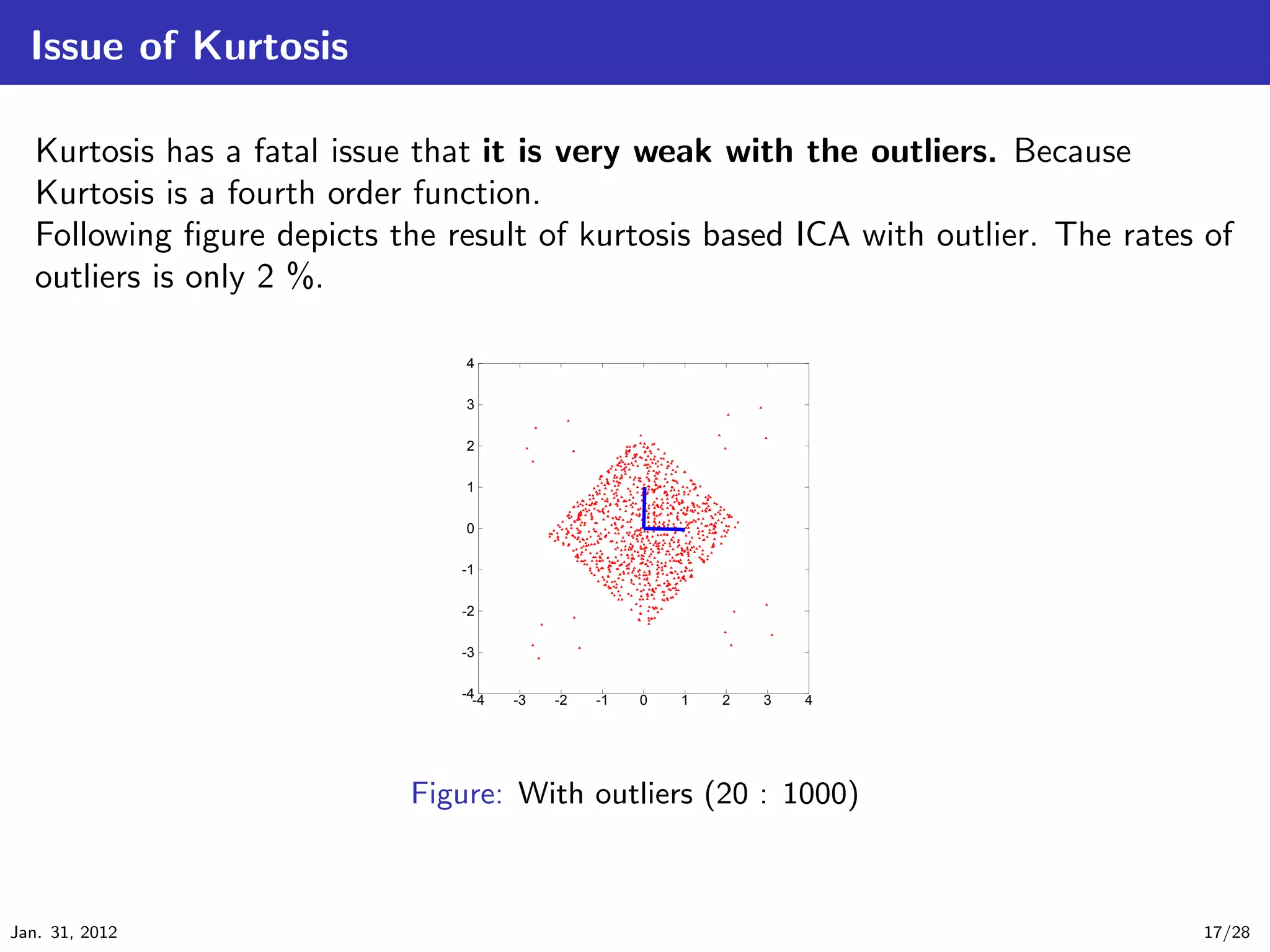
13. Maximization of Kurtosis
Kurtosis is a measures of Non-Gaussianity. Kurtosis is defined by
kurt(y) = E[y 4 ] − 3(E[y 2 ])2 . (12)
We assume that y is white (i.e. E[y] = 0, E[y 2 ] = 1 ), then
kurt(y) = E[y 4 ] − 3. (13)
We can solve the ICA problem by
ˆ
b = max |kurt(bT x(t))|. (14)
b
Jan. 31, 2012 13/28

14. Fast ICA algorithm based on Kurtosis
We consider z is a white signal given from x. And we consider to maximize the
absolute value of kurtosis as
maximize |kurt(wT z)|, s.t. wT w = 1. (15)
Differential of |kurt(wT z)| is given by
∂|kurt(wT z)| ∂
= E{(wT z)4 } − 3E{(wT z)2 }2 (16)
∂w ∂w
∂
= E{(wT z)4 } − 3{||w||2 }2 (because E(zz T ) = I) (17)
∂w
= 4sign[kurt(wT z)] E{z(wT z)3 } − 3w||w||2 (18)
Jan. 31, 2012 14/28

15. Fast ICA algorithm based on Kurtosis (cont’d)
According to the gradient method, we can obtain following algorithm:
.
Gradient algorithm based on Kurtosis .
..
w ← w + ∆w, (19)
w
w← , (20)
||w||
. ∆w ∝ sign[kurt(wT z)] E{z(wT z)3 } − 3w . (21)
.. .
.
We can see that above algorithm converge when w ∝ ∆w. And w and −w are
equivalent solution, so we can obtain another algorithm:
.
Fast ICA algorithm based on Kurtosis .
..
w ← E{z(wT z)3 } − 3w, (22)
w
w← . (23)
. ||w||
.. .
.
It is well known as a fast convergence algorithm for ICA !!
Jan. 31, 2012 15/28

16. Example
3
4
2
2
1
0 0
-1
-2
-2
-4
-3-3 -2 -1 0 1 2 3 -4 -2 0 2 4
(a) subgaussian (b) supergaussian
Figure: Example of ICA
Jan. 31, 2012 16/28

17. Issue of Kurtosis
Kurtosis has a fatal issue that it is very weak with the outliers. Because
Kurtosis is a fourth order function.
Following figure depicts the result of kurtosis based ICA with outlier. The rates of
outliers is only 2 %.
4
3
2
1
0
-1
-2
-3
-4-4 -3 -2 -1 0 1 2 3 4
Figure: With outliers (20 : 1000)
Jan. 31, 2012 17/28

18. Neg-entropy based ICA
Kurtosis is very weak with outliers.
Hence, the Neg-entropy is often used for ICA. In strictly, the approximation of
neg-entropy is often used, because it is robust for outliers.
Neg-entropy is defined by
J(y) = H(yGauss ) − H(y), (24)
where
H(y) = − py (η) log py (η)dη, (25)
and yGauss is a Gaussian distribution of µ = E(y) and σ = E((y − µ)2 ).
If y follows Gaussian distribution, then J(y) = 0.
Jan. 31, 2012 18/28

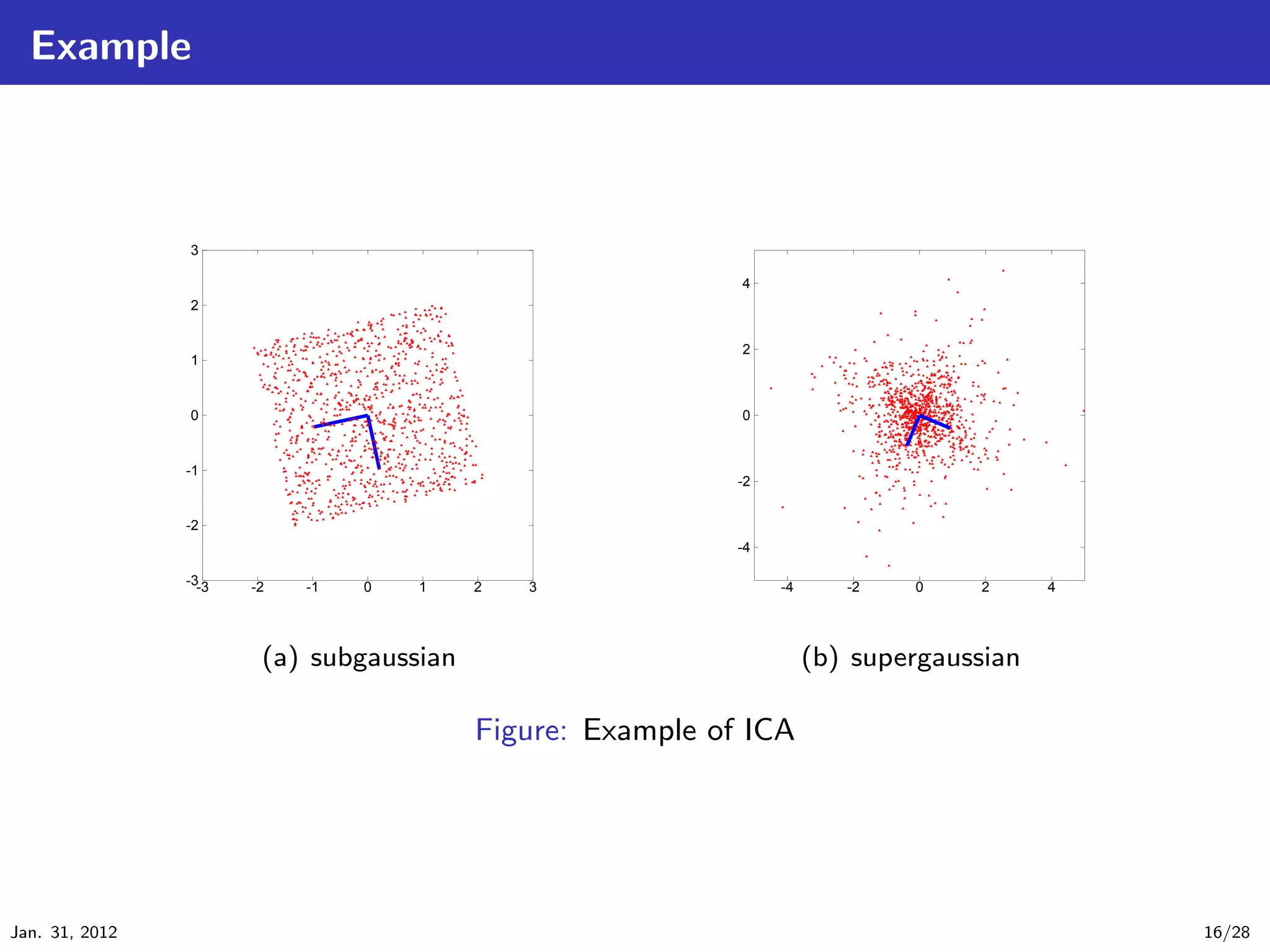
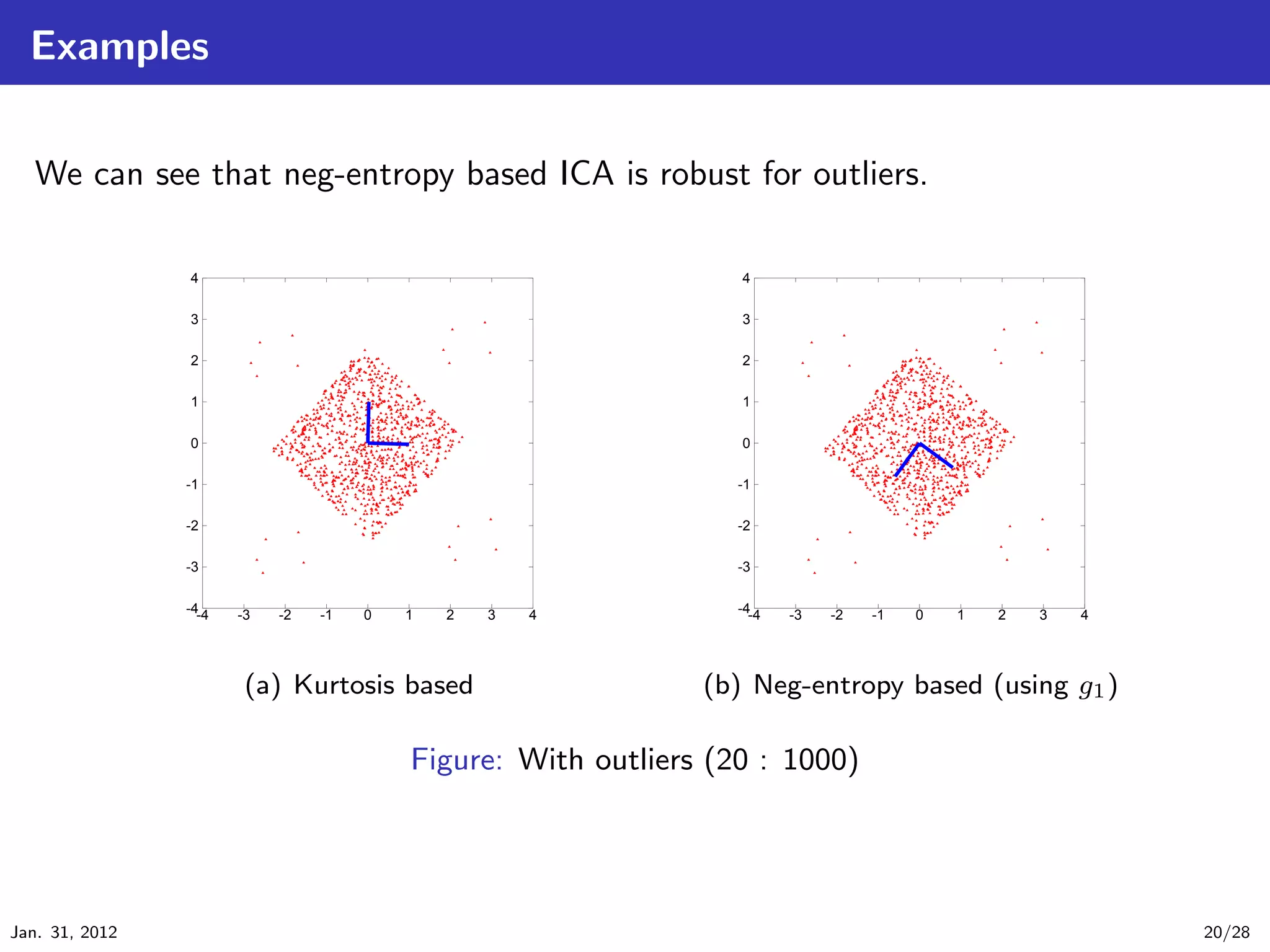
19. Fast ICA algorithm based on Neg-entropy
The approximation procedure of neg-entropy is complex, then it is omitted here.
We just introduce the fast ICA algorithm based on neg-entropy:
.
Fast ICA algorithm based on Neg-entropy .
..
w ← E[zg(wT z)] − E[g (wT z)]w (26)
w
w← (27)
. ||w||
.. .
.
where we can select functions g and g from
.
.. g1 (y) = tanh(a1 y) and g1 (y) = a1 (1 − tanh2 (a1 y)),
1
.
.. g2 (y) = y exp(−y 2 /2) and g (y) = (1 − y 2 ) exp(−y 2 /2),
2
2
...
3 g3 (y) = y 3 and g3 (y) = 3y 2 .
1 ≤ a1 ≤ 2.
Please note that (g3 , g3 ) is equivalent to Kurtosis based ICA.
Jan. 31, 2012 19/28

20. Examples
We can see that neg-entropy based ICA is robust for outliers.
4 4
3 3
2 2
1 1
0 0
-1 -1
-2 -2
-3 -3
-4-4 -3 -2 -1 0 1 2 3 4 -4-4 -3 -2 -1 0 1 2 3 4
(a) Kurtosis based (b) Neg-entropy based (using g1 )
Figure: With outliers (20 : 1000)
Jan. 31, 2012 20/28

21. Experiments: Real Image 1
(a) ob 1 (b) ob 2
(a) newyork (a) estimated signal 1
Figure: Observed Signals
(b) shanghai (b) estimated signal 2
Figure: Original Signals Figure: Estimated Signals
Jan. 31, 2012 21/28

22. Experiments: Real Image 2
(a) ob 1 (b) ob 2
(a) buta (a) estimated signal 1
Figure: Observed Signals
(b) kobe (b) estimated signal 2
Figure: Original Signals Figure: Estimated Signals
Jan. 31, 2012 22/28

23. Experiments: Real Image 2 (using filtering)
(a) ob 1 (b) ob 2
(a) buta (a) estimated signal 1
Figure: Observed Signals
(b) kobe (b) estimated signal 2
Figure: Original Signals Figure: Estimated Signals
Jan. 31, 2012 23/28

24. Experiments: Real Image 3 (using filtering)
(a) nyc (b) sha
(c) rock (d) pig (a) estimated signal 1 (b) estimated signal 2
(e) obs1 (f) obs2
(c) estimated signal 3 (d) estimated signal 4
(g) obs3 (h) obs4
Figure: Estimated Signals
Figure: Ori. & Obs.
Jan. 31, 2012 24/28

25. Approaches of ICA
In this research area, many method for ICA are studied and proposed as follow:
.
.. Criteria of ICA [Hyv¨rinen et al., 2001]
1 a
Non-Gaussianity based ICA*
Kurtosis based ICA*
Neg-entropy based ICA*
MLE based ICA
Mutual information based ICA
Non-linear ICA
Tensor ICA
...
2 Solving Algorithm for ICA
gradient method*
fast fixed-point algorithm* [Hyv¨rinen and Oja, 1997]
a
(‘*’ were introduced today.)
Jan. 31, 2012 25/28

26. Summary
I introduced about BSS problem and basic ICA techniques (Kurtosis,
Neg-entropy).
Kurtosis is weak with outliers.
Neg-entropy is proposed as a robust measure of Non-Gaussianity.
I conducted experiments of ICA using Image data.
In some case, worse results are obtained.
But I solved this issue by using differential filter.
This technique is proposed in [Hyv¨rinen, 1998].
a
We knew that the differential filter is very effective for ICA.
Jan. 31, 2012 26/28

27. Bibliography I
[Hyv¨rinen, 1998] Hyv¨rinen, A. (1998).
a a
Independent component analysis for time-dependent stochastic processes.
[Hyv¨rinen et al., 2001] Hyv¨rinen, A., Karhunen, J., and Oja, E. (2001).
a a
Independent Component Analysis.
Wiley.
[Hyv¨rinen and Oja, 1997] Hyv¨rinen, A. and Oja, E. (1997).
a a
A fast fixed-point algorithm for independent component analysis.
Neural Computation, 9:1483–1492.
Jan. 31, 2012 27/28

28. Thank you for listening
Jan. 31, 2012 28/28