This document is a compilation by Rajarshi Dutta aimed at introducing machine learning concepts for beginners, highlighting key aspects like supervised vs unsupervised learning, feature engineering, and the importance of training and test data. It covers fundamental definitions, algorithms, and evaluation metrics such as mean squared error and confusion matrices, while also emphasizing the need for balance between flexibility and bias in models. The content is designed to demystify machine learning and encourage further exploration in the field of data analytics.

1. Rajarshi Dutta
Machine Learning
and
Buzzwords
Compiled By Rajarshi Dutta
Page 1

2. Rajarshi Dutta
Table of Contents
Introduction 3
What is Machine Learning? 4
What is the difference between Statistical Learning and Machine Learning? 6
Supervised and Unsupervised Learning 7
Feature Engineering 8
Training and Test Data 9
Regression and Classification 9
MSE and Error Rate 10
Flexibility and Variance Trade off 11
Type I and Type II Error / True Positives and False Positives / Confusion Matrix 13
ROC and AUC 14
Algorithms 17
Simple Linear Regression 17
Decision Tree 21
Bagging 24
Random Forest 26
Logistic Regression 31
SVM - Support Vector Machine 37
K-Means Clustering 42
(Unsupervised Learning) 42
‘Artificial’ Neural Network 50
Summary 57
Linear Regression 58
Decision Tree 58
Random Forest 59
Logistics Regression 60
Support Vector Machine 60
Artificial Neural Network 61
K-Means Clustering 62
References 64
Page 2

3. Rajarshi Dutta
Introduction
Most of us already heard about Machine Learning. When I started learning about this I found
difficulties in finding and choosing the right material about it. There are numerous articles,
research papers, youtube videos and blogs about these but the real issue I faced was either
they are very basic or they are too advanced, they are too technical and mathematical. I could
not find that right combination of not too basic and not too technical; easy to understand.
Here, in this article I am just trying to jot down few basics and must know stuff to kick start in
this field. I am sure once you finish this article you will have lot of questions that you will tend
to find the answers for. And that is exactly the objective of this compilation; to trigger the
interest in this field of data analytics and to demystify the abstract concept. I believe the
sequence of the topic will be helpful for the people having some knowledge related to the
data engineering and analysis and want to learn about the machine learning. This article is
not for the advanced data scientists, this is for the beginners or those who want a quick
refresher.
Many people have asked me “Do I need to learn Big Data if I need to learn Machine
Learning?” - Answer is NO. Big Data gave a platform to run the machine learning code on
large scale and utilize its massive parallel processing power to have a greater performance.
Its worthwhile to mention that this domain is very large and it is constantly changing at a
break neck pace. There are several papers being published everyday. Machine Learning is
already converging towards deep learning. All these details are out of scope for now. But
keep reading and happy reading!
Oh ! One more thing, all the example codes are in R. So if you want to just try these out as
you read, please install the R and RStudio.
Page 3

4. Rajarshi Dutta
What is Machine Learning?
Machine learning is a core sub-area of artificial intelligence as it enables computers to get
into a mode of self-learning without being explicitly programmed. When exposed to new
data, computer programs, are enabled to learn, grow, change, and develop by themselves.
Tom M. Mitchell provided a widely quoted, more formal definition: "A computer program is
said to learn from experience E with respect to some class of tasks T and performance
measure P if its performance at tasks in T, as measured by P, improves with experience E.”
This definition is notable for its defining machine learning in fundamentally operational rather
than cognitive terms, thus following Alan Turing's proposal in his paper "Computing
Page 4

5. Rajarshi Dutta
Machinery and Intelligence", that the question "Can machines think?" be replaced with the
question "Can machines do what we (as thinking entities) can do?". In the proposal he
explores the various characteristics that could be possessed by a thinking machine and the
various implications in constructing one.
In our real world, there are several places we use machine learning - e.g. Face recognition in
the digital camera, movie recommendation in Netflix, product recommendation in Amazon,
AirBnB uses machine learning for fraud detection, it is being widely used in automated
trading etc.
Page 5

6. Rajarshi Dutta
What is the difference between Statistical Learning and
Machine Learning?
Statistics is interested in learning something about data, for example, which have been
measured as part of some biological experiment. Statistics is necessary to support or reject
hypothesis based on noisy data, or to validate models, or make predictions and forecasts. But
the overall goal is to arrive at new scientific insight based on the data.
In Machine Learning, the goal is to solve some complex computational task by 'letting the
machine learn'. Instead of trying to understand the problem well enough to be able to write a
program which is able to perform the task (for example, handwritten character recognition),
you instead collect a huge amount of examples of what the program should do, and then run
an algorithm which is able to perform the task by learning from the examples. Often, the
learning algorithms are statistical in nature. But as long as the prediction works well, any kind
of statistical insight into the data is not necessary.
Page 6

7. Rajarshi Dutta
Machine learning requires no prior assumptions about the underlying relationships between
the variables. You just have to throw in all the data you have, and the algorithm processes the
data and discovers patterns, using which you can make predictions on the new data set.
Machine learning treats an algorithm like a black box, as long it works. It is generally applied
to high dimensional data sets, the more data you have, the more accurate your prediction is.
In contrast, statisticians must understand how the data was collected, statistical properties of
the estimator (p-value, unbiased estimators), the underlying distribution of the population
they are studying and the kinds of properties you would expect if you did the experiment
many times. You need to know precisely what you are doing and come up with parameters
that will provide the predictive power. Statistical modeling techniques are usually applied to
low dimensional data sets.
Supervised and Unsupervised Learning
In supervised learning, the output datasets are provided which are used to train the machine
and get the desired outputs whereas in unsupervised learning no datasets are provided,
instead the data is clustered into different classes . You are a kid, you see different types of
animals, your father tells you that this particular animal is a dog…after him giving you tips few
times, you see a new type of dog that you never saw before - you identify it as a dog and not
as a cat or a monkey or a potato. - This is Supervised Learning. here you have a teacher to
guide you and learn concepts, such that when a new sample comes your way that you have
not seen before, you may still be able to identify it.
Contrary, if you are training your machine learning task only with a set of inputs, it is called
unsupervised learning, which will be able to find the structure or relationships between
different inputs. Most important unsupervised learning is clustering, which will create different
cluster of inputs and will be able to put any new input in appropriate cluster. You go bag-
packing to a new country, you did not know much about it - their food, culture, language etc.
However from day 1, you start making sense there, learning to eat new cuisines including
what not to eat, find a way to that beach etc. This is an example of unsupervised classification,
where you have lots of information but you did not know what to do with it initially. A major
distinction is that, there is no teacher to guide you and you have to find a way out on your
own. Then, based on some criteria you start churning out that information into groups that
makes sense to you.
Page 7

8. Rajarshi Dutta
Feature Engineering
This is the real meat of the Machine Learning. The Model is as good as your features are.
“….Feature engineering is the process of transforming raw data into features that better
represent the underlying problem to the predictive models, resulting in improved model
accuracy on unseen data….”
The features are the critical attributes or predictors based on which the model will predict the
output. This step involves a lot of data mining and data discoveries. In general the attributes
can be of two types - Categorical (Red , Green, Amber or 1,0 Types) and Continuous
Numbers. There are lot of ways one can extract features out of large number of attributes.
Most commonly used is to derive the correlation coefficient of the individual features to the
problem and take the critically correlated features. To identify the meaningful correlation and
filter them out we need the domain experts. (Note: the two variables can be 99% correlated
and they might not have any common relevance. E.g. I notice that whenever I put my new
shoes on , it rains. Wearing new shoes and raining are almost 90% correlated but it does not
have any significance and relevance.)
Several algorithms like ANN (Artificial Neural Network) works better on the features if they are
scaled between 0 and 1. One way to scale them is the Min-Max method. For any continuous
numbers N,
Scaled N = {N - Min(N)}/{Max(N) - Min(N)}
This will scan the number between 0 and 1. So you will know what is the high value and what
is the low value.
Univariate : Take Individual Variables , for the categorical - create the count(*) stats. For the
continuous variable create the chart for min,max, stddev, mean,median and mode
Bi Variate : two continuous variable and their correlation. Two categorical variables and their
two way chart or stack bar.
Missing value Treatment : Missing data in the training data set can reduce the power / fit of a
model or can lead to a biased model because we have not analyzed the behavior and
relationship with other variables correctly. It can lead to wrong prediction or classification. If
Page 8

9. Rajarshi Dutta
possible identify the missing value reason , fix the actual DQ issue or discard the records or
populate the meaningful default value with consolation with the domain expert.
Outlier treatment: Outliers can drastically change the results of the data analysis and
statistical modeling. understand the reason for the outliers - it can be univariate or
multivariate - based on one variable or based on multiple variables. There are several
algorithms which don't care about the outliers e.g. SVM (Support Vector Machine) , whereas
the Logistic Regression will provide wrong results if the dataset has the outliers.
Training and Test Data
A general practice is to split your data into a training and test set. You train/tune your model
with your training set and test how well it generalizes to data it has never seen before with
your test set.
Your model's performance on your test set will provide insights on how your model is
performing and allow you to work out issues like bias vs variance trade-offs.
Like all experiments, most of the time you will want to do random sampling to obtain training
and test sets that are more or less representative population samples.However you should be
aware of issues like class imbalance where for example the frequency of one class dominates
in your target values.
In such cases, you probably have to do stratified data splitting based on the classes for your
test and training set to have the same proportion of both classes.
When your number of observations in your dataset is very small, there have also been strong
cases made to not split the data as less data will have impact on the predictive power of your
model.
Regression and Classification
Variables can be characterized as either quantitative or qualitative (also known as
categorical). Quantitative variables take on numerical values. Examples include a person’s
age, height, or income, the value of a house, and the price of a stock. In contrast, qualitative
variables take on values in one of K different classes, or categories. Examples of qualitative
variables include a person’s gender (male or female), the brand of product purchased (brand
Page 9

10. Rajarshi Dutta
A, B, or C), whether a person defaults on a debt (yes or no). We tend to refer to problems with
a quantitative response as regression problems, while those involving a qualitative response
are often referred to as classification problems.
MSE and Error Rate
This is a very important measure to understand the quality of the fit of the model. In order to
evaluate the performance of a statistical learning method on a given data set, we need some
way to measure how well its predictions actually match the observed data. That is, we need to
quantify the extent to which the predicted response value for that observation. In the
Regression setting most commonly used measure is MSE ( Mean Squared Error). In high level
this is the average squared distance between the predicted data point and the actual data
point. The red dots are the actual data points and the blue line is the regression line. So if you
traverse along the line you can tell what would be the Y value give X (i.e. predicted value).
And the distance between the red dots (actual data point) and the predicted regression line
is the error. If we average all the data points’ squared distance - we get the MSE.
Yi is actual point and the f^(Xi) is the predicted value.
Page 10

11. Rajarshi Dutta
Error rate is the measure for the Classifier Problem - where the prediction is either YES or NO.
Or the classify the data into the classes A,B or C etc. This measure tells how good the
classification is when it comes to predict the datasets into classes.
Lets say in a real datasets , there are N number of male. But the model predicts there are M
males. So in general the error rate is 1 - M/N. So out of N, model was able to predict M. A
good classifier is one for which the test error is smallest. The other way we an calculate is for
each data point , if the model classifies correctly we tag them 0 else 1. And then do the
average across all population and that is the number we call error rate.
Flexibility and Variance Trade off
A model is considered to be flexible when it can traverse along with the data points.
Generally speaking these kinds of models show high variance - meaning with every new set
of data the model prediction will change. Now consider the simple linear regression model -
a regression line. This model is not flexible enough and very good with the linear set of data
and this model shows high bias in nature. So choosing a model for the problem means
choosing a right balance between variance(flexibility) and bias(relatively rigid) model - this is
a trade off. The right choice will result in no overfitting.
Now the question is how to do this? We will touch upon this point very briefly to share this
idea. In general this is
Page 11

12. Rajarshi Dutta
The linear regression line (orange curve), and two smoothing spline fits (blue and green curves). Right: Training
MSE (grey curve), test MSE (red curve), and minimum possible test MSE over all methods (dashed line). Squares
represent the training and test MSEs for the three fits shown in the left-hand panel.
done with lot of cross validation and test the model with different set of parameters and test
against the test data.
From the Flexibility ~ MSE curve - We see as we increase the flexibility of the model the
training error goes low (the grey line)- which is obvious because as we provide more data the
flexible model will try to traverse as close as possible to the data points but it does not
guarantee that it will work better with the unseen data i.e. Test data - this problem is called
Over Fitting. Training MSE is definitely not the measure or the estimate for the test MSE.
Now in the same figure, if we focus on the red curve i.e. for the test data - it shows that as we
increase the flexibility the MSE starts going down but after a certain point it moves up. The
optimal point of the flexibility is where we see the deflection. In this fig - the Flexibility 5.
Now if we plot MSE, Variance and Bias all three in a same plot -
Page 12

13. Rajarshi Dutta
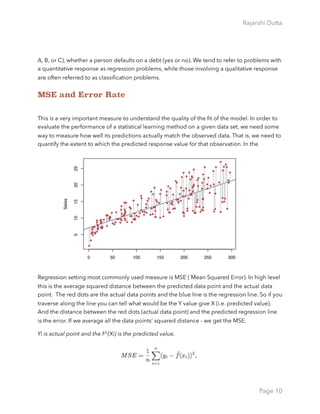
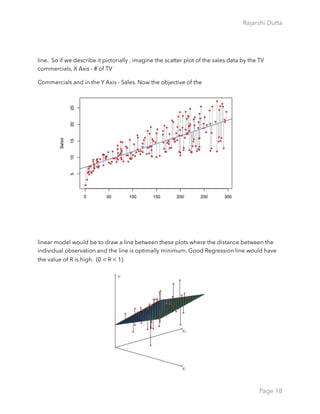
As a general rule, as we use more flexible methods, the variance will increase and the bias will
decrease. The relative rate of change of these two quantities determines whether the test
MSE increases or decreases. As we increase the flexibility of a class of methods, the bias
tends to initially decrease faster than the variance increases. Consequently, the expected test
MSE declines. However, at some point increasing flexibility has little impact on the bias but
starts to significantly increase the variance. When this happens the test MSE increases. In
order to minimize the expected test error, we need to select a statistical learning method that
simultaneously achieves low variance and low bias.
Type I and Type II Error / True Positives and False
Positives / Confusion Matrix
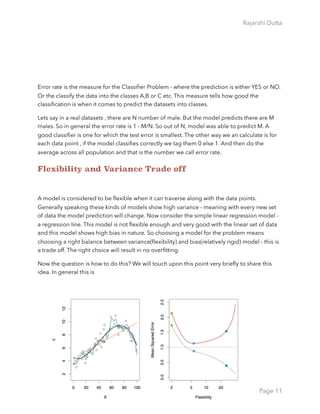
In the field of machine learning and specifically the problem of statistical classification, a
confusion matrix, also known as an error matrix,[4] is a specific table layout that allows
visualization of the performance of an algorithm, typically a supervised learning one (in
unsupervised learning it is usually called a matching matrix).
If a classification system has been trained to distinguish between cats, dogs and rabbits, a
confusion matrix will summarize the results of testing the algorithm for further inspection.
Page 13

14. Rajarshi Dutta
Assuming a sample of 27 animals — 8 cats, 6 dogs, and 13 rabbits, the resulting confusion
matrix could look like the table below:
Assuming the confusion matrix above, its corresponding table of confusion, for the cat class,
would be:
ROC and AUC
The most commonly reported measure of classifier performance is accuracy: the percent of
correct classifications obtained.
The true positive rate (also called hit rate and recall or sensitivity) of a classifier is estimated as
The false positive rate (also called false alarm rate) of the classifier is
Page 14

15. Rajarshi Dutta
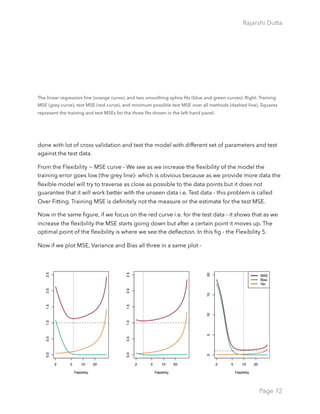
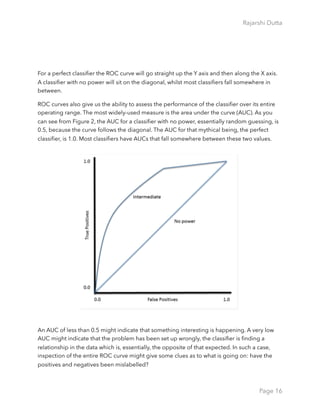
Additional term associated with ROC curves is
Let’s consider a sample of patients data and the objective is to classify whether the patients
have cancers or not. E.g. The Algorithm f will produce the score from low (0.0) [Without
Cancer] to high (1.0) [With Cancer]
Most classifiers produce a score, which is then thresholded to decide the classification. If a
classifier produces a score between 0.0 (definitely negative) and 1.0 (definitely positive), it is
common to consider anything over 0.5 as positive. But this dashed line depends on the
experimenter - where she wants to draw the threshold. If we draw the threshold at 0.0 - which
means we will correctly classify all the positive cases but incorrectly classify all the negative
cases. And similarly if we draw the threshold at we will correctly classify all the negative cases
and incorrectly classify the positive ones. While we
gradually move the threshold from 0.0 to 1.0 we will
have different TPR (True Positive Rate) and FPR(false
Positive Rate) at each threshold point; progressively
decreasing the number of false positives and increasing
the number of true positives. If we plot these series of
TPR and FPR (Y Axis - TPR and X Axis - FPR) we get the
ROC (Receiver operating characteristic) Curve. AUC is
the Area under the cure.
Page 15

16. Rajarshi Dutta
For a perfect classifier the ROC curve will go straight up the Y axis and then along the X axis.
A classifier with no power will sit on the diagonal, whilst most classifiers fall somewhere in
between.
ROC curves also give us the ability to assess the performance of the classifier over its entire
operating range. The most widely-used measure is the area under the curve (AUC). As you
can see from Figure 2, the AUC for a classifier with no power, essentially random guessing, is
0.5, because the curve follows the diagonal. The AUC for that mythical being, the perfect
classifier, is 1.0. Most classifiers have AUCs that fall somewhere between these two values.
An AUC of less than 0.5 might indicate that something interesting is happening. A very low
AUC might indicate that the problem has been set up wrongly, the classifier is finding a
relationship in the data which is, essentially, the opposite of that expected. In such a case,
inspection of the entire ROC curve might give some clues as to what is going on: have the
positives and negatives been mislabelled?
Page 16

17. Rajarshi Dutta
Algorithms
Simple Linear Regression
Linear Regression is a very simple approach for supervised learning. This method is a useful
tool for predicting the quantitative response. A quantitative response Y on the basis of a
single predictor variable X. It assumes that approximately Y and X have a linear relationship.
Y ≈ β0 + β1X
E.g. If we think that the sales of the product has a linear relationship with the TV commercials,
Sales ≈ β0 + β1*TVCommercials
Now, to predict based on this model, we need to know the value of the β0 and β1. β0 is the
intercept and the β1 is the slope. By doing the linear regression, the algorithm will provide
the estimate of these two coefficients and their standard error, t-statistics and the p-value.
Based on these two statistical measure we can tell how good these measures are. Generally,
value of these two variables hypothesis tested.
Hypothesis :
H0 (Null Hypothesis): There is no relationship between X and Y
Ha (Alternate Hypothesis): There is some relationship between X and Y . Mathematically, this
corresponds to testing
H0 : β1 = 0
Ha : β1 != 0
In general practice, we don't do all these tests for every linear model. Rather we focus on R
(Coefficient of Regression) - which provides the information how good fit is the Regression
Page 17

18. Rajarshi Dutta
line. So if we describe it pictorially , imagine the scatter plot of the sales data by the TV
commercials, X Axis - # of TV
Commercials and in the Y Axis - Sales. Now the objective of the
linear model would be to draw a line between these plots where the distance between the
individual observation and the line is optimally minimum. Good Regression line would have
the value of R is high. (0 < R < 1).
Page 18

19. Rajarshi Dutta
In a three-dimensional setting, with two predictors and one response,the least squares regression line becomes a
plane. The plane is chosen to minimize the sum of the squared vertical distances between each
observation(shown in red) and the plane.
If we add one more predictor variable e.g. RadioCommercials, then Linear model will try to
draw a 3-Dimensional Plane. Similarly we can keep adding the significant predictor for the
model. This is called Multiple Linear Regression.
sales = β0 + β1 × TV + β2 × radio + E(Error)
Now, in this example, we play the role of data analyst who works for Motor Trend, a magazine
about the automobile industry. Looking at a data set of a collection of cars, we are interested
in exploring the relationship between a set of variables and miles per gallon (MPG)
(outcome). We are trying to answer the following two questions - Question1: “Is an automatic
or manual transmission better for MPG?”, Question2: “Quantify the MPG difference between
automatic and manual transmissions.”
> library(datasets)
> data(mtcars)
> head(mtcars,5)
mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
fit1 <- lm(mpg ~ factor(am), data=mtcars)
lm is the linear model. In other way we are creating the linear model where the predicted
variable is mpg and the predictor is am (Automatic or manual - this is a categorical variable
{0,1} and hence we factored it)
summary(fit1)
Page 19

20. Rajarshi Dutta
Call:
lm(formula = mpg ~ factor(am), data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-9.3923 -3.0923 -0.2974 3.2439 9.5077
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 17.147 1.125 15.247 1.13e-15 ***
factor(am)1 7.245 1.764 4.106 0.000285 ***
Residual standard error: 4.902 on 30 degrees of freedom
Multiple R-squared: 0.3598, Adjusted R-squared: 0.3385
F-statistic: 16.86 on 1 and 30 DF, p-value: 0.000285
Now as we mentioned in the above , the p-value is used to do the hypothesis test. With a p-
value being very small at 0.000285, we reject the null hypothesis and we say that there is
linear correlation between the predictor variable am and mpg. We also see from this
summary that R-Squared is 0.338 also This means that our model only explains 33.8% of the
variance. We can also say from the summary that group mean for mpg is 17.147 for automatic
transmission and 24.49 = 17.147 + 7.24*1 for manual transmission cars.
Since there are more variables in this dataset that also look like they have linear correlations
with dependent variable mpg, we will explore a multivariable regression model next. We will
not add wt, hp, dis and cal as the predictor and see if we get the better model.
fit2 <- lm(formula = mpg ~ am + wt + hp + disp + cyl, data = mtcars)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 38.20280 3.66910 10.412 9.08e-11 ***
am 1.55649 1.44054 1.080 0.28984
wt -3.30262 1.13364 -2.913 0.00726 **
hp -0.02796 0.01392 -2.008 0.05510 .
disp 0.01226 0.01171 1.047 0.30472
Page 20

21. Rajarshi Dutta
cyl -1.10638 0.67636 -1.636 0.11393
Residual standard error: 2.505 on 26 degrees of freedom
Multiple R-squared: 0.8551, Adjusted R-squared: 0.8273
F-statistic: 30.7 on 5 and 26 DF, p-value: 4.029e-10
We now got the adjusted R-Squared 83%. So this model is better than the previous one and
this explains the 83% of the data.
Decision Tree
We cannot learn machine learning without knowing “What is Decision Tree and Random
Forest”. So, here we will take a closer look at these algorithms one by one.
A decision tree is a flow-chart-like structure, where each internal (non-leaf) node denotes a
test on an attribute, each branch represents the outcome of a test, and each leaf (or terminal)
node holds a class label. The topmost node in a tree is the root node. There are many specific
decision-tree algorithms.
Page 21

22. Rajarshi Dutta
The final result is a tree with decision nodes and leaf nodes. A decision node (e.g., Outlook)
has two or more branches (e.g., Sunny, Overcast and Rainy). Leaf node (e.g., Play) represents
a classification or decision. The topmost decision node in a tree which corresponds to the
best predictor called root node.
The above example of decision making is of type Classification Tree where the predicted
outcome is the class to which the data belongs {YES|NO}. Regression Tree analysis is when the
predicted outcome can be considered a real continuous number (e.g. Based on the number
of years of experience and age, predict the Salary of a Baseball Player).
Now lets take a very generic example : Sorting the marbles.
We have total 11 marbles - 6 Red and 5 Green marbles. In each level we are splitting the
marbles based on some features and order them according to their colors. In the first split,
the marbles are not ordered properly - both nodes have the Red and Green marbles. But, at
the last right split (S*) , the marbles are sorted perfectly - greens and reds are separated.
Page 22
S*

23. Rajarshi Dutta
However, the left split still has some impurity. The feature based on which the split S*
happened is powerful - an important feature. Now we can say - a good attribute prefers
attributes that split the data so that each successor node is as pure as possible i.e. the
distribution of examples in each node is so that it mostly contains examples of a single class.
We want a measure that prefers attributes that have a high degree of “order“:
● Maximum order: All examples are of the same class (in our example the two right
most leaves - Zero Entropy )
● Minimum order: All classes are equally likely (in our example - Level 1 right node,
50% probability for both Red and Green - Maximum Entropy)
Yes!! These seem little deeper in technical and mathematical but believe me this is not as
difficult as these sound. We would need these concept when we would understand the
Feature Importance in Random Forest.
Now, let’s understand the Entropy , Information Gain and Gini Index.
Entropy is a measure for (un-) orderedness
Entropy is the amount of information that is contained (Maximum when the odds are even or
the probability is 0.5). All examples of the same class (Probability is 1.0) , No Information;
Entropy is 0.
When an attribute A splits the set S into subsets Sn, we compute the average entropy and
compare the sum to the entropy of the original set S. The attribute that maximizes the
difference (Information Gain) is selected (i.e. the attribute that reduces the un-orderedness
most). Maximizing Information Gain is equivalent to minimizing average entropy.
Gini Index is a very popular alternative to Information Gain.
Gini impurity is a measure of how often a randomly chosen element from the set would be
incorrectly labeled if it was randomly labeled according to the distribution of labels in the
subset. Gini impurity can be computed by summing the probability Pi of an item with label i
being chosen times the probability 1-Pi of a mistake in categorizing that item. It reaches its
minimum (zero) when all cases in the node fall into a single target category.
Page 23

24. Rajarshi Dutta
Which model is better - Linear Model or Tree? It depends on the problem at hand. If the
relationship between the features and the response is well approximated by a linear model
an approach such as linear regression will likely work well, and will outperform a method such
as a regression tree that does not exploit this linear structure. If instead there is a highly non-
linear and complex relationship between the features and the response, then decision trees
may outperform classical approaches.
Bagging
The decision trees suffer from high variance (more flexible algorithms have high variance, low
bias and less flexible algorithm e.g. Linear Model has low variance but has high bias). This
Page 24

25. Rajarshi Dutta
means that if we split the training data into two parts at random, and fit a decision tree to both
halves, the results that we get could be quite different. In contrast, a procedure with low
variance will yield similar results if applied repeatedly to distinct data sets; linear regression
tends to have low variance. Bootstrap aggregation, or bagging, is a general-purpose
procedure for reducing the variance of a statistical learning method.
Top Row: A two-dimensional classification example in which the true decision boundary is linear, and is indicated
by the shaded regions. A classical approach that assumes a linear boundary (left) will outperform a decision tree
Page 25

26. Rajarshi Dutta
that performs splits parallel to the axes (right). Bottom Row: Here the true decision boundary is non-linear. Here a
linear model is unable to capture the true decision boundary (left), whereas a decision tree is successful (right).
Recall that given a set of n independent observations Z1,...,Zn, each with variance σ2, the
variance of the mean Z ̄ of the observations is given by σ2/n. In other words, averaging a set
of observations reduces variance. Hence a natural way to reduce the variance and hence
increase the prediction accuracy of a statistical learning method is to take many training sets
from the population, build a separate prediction model using each training set, and average
the resulting predictions. We can bootstrap, by taking repeated samples from the (single)
training data set. In this approach we generate B different bootstrapped training data sets.
We then train our method on the b-th bootstrapped training set in order to get the predicted
value on the b-th training set, and finally average all the predictions, to obtain final predicted
value for the whole training set.
This is called bagging.
Ok. Let’s take a pause here. Isn’t it the same thing as we do in Random Forest? Creating
multiple trees from the same training set and average it out. Then why do we have two
different algorithms - Bagging and Random Forest? We will see in the next section - Random
Forest.
Random Forest
Random forests provide an improvement over bagged trees by way of a small tweak that de-
correlates the trees. In other words, in building a random forest, at each split in the tree, the
algorithm is not even allowed to consider a majority of the available predictors. This may
sound crazy, but it has a clever rationale. Suppose that there is one very strong predictor in
the data set, along with a number of other moderately strong predictors. Then in the
collection of bagged trees, most or all of the trees will use this strong predictor in the top
split. Consequently, all of the bagged trees will look quite similar to each other. Hence the
predictions from the bagged trees will be highly correlated. Unfortunately, averaging many
highly correlated quantities does not lead to as large of a reduction in variance as averaging
many uncorrelated quantities. In particular, this means that bagging will not lead to a
substantial reduction in variance over a single tree in this setting.
Page 26

27. Rajarshi Dutta
Random forests overcome this problem by forcing each split to consider only a subset of the
predictors. Therefore, on average (p − m)/p of the splits will not even consider the strong
predictor, and so other predictors will have more of a chance. We can think of this process as
de-correlating the trees, thereby making the average of the resulting trees less variable and
hence more reliable.
The main difference between bagging and random forests is the choice of predictor subset
size m. For instance, if a random forest is built using m = p, then this amounts simply to
bagging.
Now, in this example we will predict the income of the individuals, whether the income is
>50K or <=50K , an example of a classifier problem.
#Download the data into R
data = read.table("http://archive.ics.uci.edu/ml/machine-
learning-databases/adult/
adult.data",sep=",",header=F,col.names=c("age", "type_employer",
"fnlwgt", "education","education_num","marital", "occupation",
"relationship", "race","sex","capital_gain", "capital_loss",
"hr_per_week","country", “income”))
#Get these libraries loaded in the session
Page 27

28. Rajarshi Dutta
library(randomForest)
library(ROCR)
#Divide the datasets into train and test datasets
ind <- sample(2,nrow(data),replace=TRUE,prob=c(0.7,0.3))
trainData <- data[ind==1,]
testData <- data[ind==2,]
#Running the RF Algorithm with 100 Trees
adult.rf <-randomForest(income~.,data=trainData, mtry=2,
ntree=100,keep.forest=TRUE,importance=TRUE,test=testData)
print(adult.rf)
#Output
#varImpPlot will plot the importance of the features. The
importance of the features are relative to each other.
varImpPlot(adult.rf)
Page 28

29. Rajarshi Dutta
#Get the probability score for the output label and download
this data
adult.rf.pr = predict(adult.rf,type=“prob”,newdata=testData)[,2]
write.csv(adult.rf.pr, file=“Test_Prob.csv”)
#Sample output of the file
# Performance of the prediction, ROC Curve and AUC
adult.rf.pred = prediction(adult.rf.pr, testData$income)
adult.rf.perf = performance(adult.rf.pred,"tpr","fpr")
Page 29

30. Rajarshi Dutta
plot(adult.rf.perf,main="ROC Curve for Random
Forest",col=2,lwd=2)
abline(a=0,b=1,lwd=2,lty=2,col=“gray")
adult.rf.auc = performance(adult.rf.pred,"auc")
AUC <- adult.rf.auc@y.values[[1]]
print(AUC)
[1] 0.8948409
Page 30

31. Rajarshi Dutta
Logistic Regression
Logistic regression is a statistical method for analyzing a dataset in which there are one or
more independent variables that determine an outcome. The outcome is measured with a
dichotomous variable (in which there are only two possible outcomes) e.g. {YES|NO} - Answer
to classification problems.
A group of 20 students spend between 0 and 6 hours studying for an exam. How does the
number of hours spent studying affect the probability that the student will pass the exam?
Probability of passing exam, given the hours of study.
P(Y=Passing Exam|X=Hours of Study)
The reason for using logistic regression for this problem is that the dependent variable pass/
fail represented by "1" and "0" are not cardinal numbers. If the problem were changed so that
pass/fail was replaced with the grade 0–100 (cardinal numbers), then simple regression
analysis could be used.
The table shows the number of hours each student spent studying, and whether they passed
(1) or failed (0).
The logistic regression analysis gives the following output. A sigmoid curve.
Page 31

32. Rajarshi Dutta
This table shows the probability of passing the exam for several values of hours studying.
If you imagine to solve this problem with a linear regression, the regression line would be
very much bias and hence results in significant error rate. So in high level, we can say these
categorical dependent variable related problems can be addressed with Logistics
Regression.
Page 32

33. Rajarshi Dutta
Now we will take a little deep dive in implementing this model in R. Kaggle - Titanic dataset is
very famous datasets in the machine learning world. We will use this example for learning this
algorithm.
The dataset (training) is a collection of data about some of the passengers (889 to be
precise), and the goal of the competition is to predict the survival (either 1 if the passenger
survived or 0 if they did not) based on some features such as the class of service, the sex, the
age etc.
Page 33

34. Rajarshi Dutta
## Loading Training Data ##
training.data.raw <- read.csv("train.csv",header=T,na.strings=c(""))
## Now we need to check for missing values and look how many unique
values there are
## for each variable using the sapply() function which applies the
function passed
## as argument to each column of the dataframe.
sapply(training.data.raw,function(x) sum(is.na(x)))
# getting only the relevant columns
data <- subset(training.data.raw,select=c(2,3,5,6,7,8,10,12))
# Now note that we have missing values on Age also and that needs to
be
# fixed. One possible way to fix is replace the nulls with the Mean,
Median or Mode.
data$Age[is.na(data$Age)] <- mean(data$Age,na.rm=T)
# Treatment on the categorical variables. in R when we read the file
via
Page 34

35. Rajarshi Dutta
# read.table() or read.csv() by default it encodes the categorical
is.factor(data$Sex)
is.factor(data$Embarked)
train <- data[1:800,]
test <- data[801:889,]
# model training with the training data
model <- glm(Survived ~.,family=binomial(link='logit'),data=train)
summary(model)
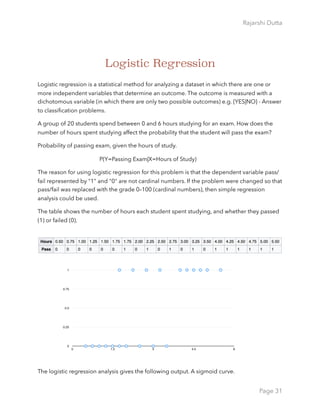
Now we can analyze the fitting and interpret what the model is telling us.
First of all, we can see that SibSp, Fare and Embarked are not statistically significant. As for the
statistically significant variables, sex has the lowest p-value suggesting a strong association of
the sex of the passenger with the probability of having survived. The negative coefficient for
this predictor suggests that all other variables being equal, the male passenger is less likely to
have survived. Remember that in the logit model the response variable is log odds: ln(odds)
Page 35

36. Rajarshi Dutta
= ln(p/(1-p)) = a*x1 + b*x2 + … + z*xn. Since male is a dummy variable, being male reduces
the log odds by 2.75 while a unit increase in age reduces the log odds by 0.037.
library(ROCR)
p <- predict(model, newdata=subset(test,select=c(2,3,4,5,6,7,8)),
type="response")
pr <- prediction(p, test$Survived)
prf <- performance(pr, measure = "tpr", x.measure = "fpr")
plot(prf)
auc <- performance(pr, measure = "auc")
auc <- auc@y.values[[1]]
auc
0.8621652
Page 36

37. Rajarshi Dutta
SVM - Support Vector Machine
SVMs have been shown to perform well in a variety of settings, and are often considered one
of the best “out of the box” classifiers. Before we try to understand SVM, let us first set the
context - let’s do some ground work.
What is Hyperplane?
In a p-dimensional space, a hyperplane is a flat affine subspace of dimension p − 1.1
For
instance, in two dimensions, a hyperplane is a flat one-dimensional subspace—in other words,
a line.
Now consider the hyperplane separating the classes of the observation. In the above figure
(top - left) we can draw more than one hyperplane to classify the blue and red dots. Out of
the three hyperplanes we choose only one optimal (top-right figure) - we choose the
hyperplane where the average distance between the dots and the hyperplane is the largest.
So this Hyperplane is called the maximal margin hyperplane - the separating hyperplane that
is farthest from the training observations. We can then classify a test observation based on
which side of the maximal margin hyperplane it lies. This is known as the maximal margin
classifier.
Page 37

38. Rajarshi Dutta
What is Support Vectors?
In the above figure, we see there are three observation data points are equidistant from the
maximal margin hyperplane. If these points move the maximal margin hyperplane will also
shift its place. These observations are called Support Vectors. Now remember the Variance
and Bias of a model and try to connect that concept with this model. If you have more
support vectors the model has less variance but high bias. In Support Vector Machine model
we have a parameter C (details are out of scope) through which we can tune these two
important factors for the SVM model. If C is small, then there will be fewer support vectors
and hence the resulting classifier will have low bias but high variance. We will see in the
example how we can choose the right value of C.
Page 38

39. Rajarshi Dutta
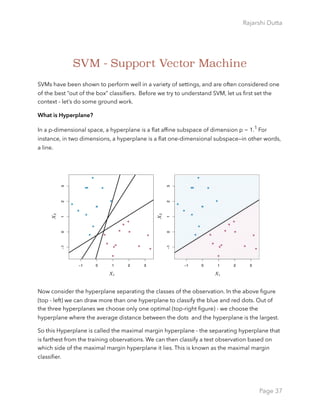
What is Support Vector Machine?
Most cases we find our observations cannot be separated by a linear approach.
In this figure (top-left), the Support vector classifier does the poor job. Where as in the top-
middle and the right most figure we see the perfect non-linear classification.
The support vector machine (SVM) is an extension of the support vector classifier that results
from enlarging the feature space in a specific way, using kernels. We will now discuss this
extension, the details of which are somewhat complex and beyond the scope of this book.
We want to enlarge our feature space in order to accommodate a non-linear boundary
between the classes. The kernel approach that we describe here is simply an efficient
computational approach for enacting this idea. In the top-middle figure - the kernel of degree
3 applied to the non-linear data and in the top right figure the radial kernel was applied. We
can see , either kernel was capable to capture the boundaries.
library(e1071)
set.seed(1)
x=matrix(rnorm(200*2), ncol=2)
x[1:100,]=x[1:100,]+2
x[101:150,]=x[101:150,]-2
Page 39

40. Rajarshi Dutta
y=c(rep(1,150),rep(2,50))
dat=data.frame(x=x,y=as.factor(y))
plot(x, col=y)
svmfit=svm(y~.,data=dat[train,], kernel="radial", gamma=2,cost =1)
plot(svmfit , dat[train ,])
tune.out=tune(svm, y~., data=dat[train,], kernel="radial",
ranges=list(cost=c(0.1,1,10,100,1000),
gamma=c(0.5,1,2,3,4) ))
summary(tune.out)
Page 40

41. Rajarshi Dutta
tune function stores the best parameter. So you can just call the sum with these parameters.
Page 41

42. Rajarshi Dutta
K-Means Clustering
(Unsupervised Learning)
In unsupervised learning there are two broad categories - PCA(Principal Component Analysis)
and Clustering method. In this section we will focus on Clustering Method; K-Means
Clustering Algorithm.
Clustering refers to a very broad set of techniques for finding subgroups, or clusters, in a data
set. When we cluster the observations of a data set, we seek to partition them into distinct
groups so that the observations within each group are quite similar to each other, while
observations in different groups are quite different from each other. Clustering looks to find
homogeneous subgroups among the observations.
For instance, suppose that we have a set of n observations, each with p features. The n
observations could correspond to tissue samples for patients with breast cancer, and the p
features could correspond to measurements collected for each tissue sample; these could be
clinical measurements, such as tumor stage or grade, or they could be gene expression
measurements. We may have a reason to believe that there is some heterogeneity among the
n tissue samples; for instance, perhaps there are a few different un- known subtypes of breast
cancer. Clustering could be used to find these subgroups. This is an unsupervised problem
because we are trying to dis- cover structure—in this case, distinct clusters—on the basis of a
data set. The goal in supervised problems, on the other hand, is to try to predict some
outcome vector such as survival time or response to drug treatment.
K-means clustering is a type of unsupervised learning - clustering method, which is used
when you have unlabeled data (i.e., data without defined categories or groups). The goal of
this algorithm is to find groups in the data, with the number of groups represented by the
variable K. The algorithm works iteratively to assign each data point to one of K groups based
on the features that are provided. Data points are clustered based on feature similarity. The
results of the K-means clustering algorithm are:
1. The centroids of the K clusters, which can be used to label new data
2. Labels for the training data (each data point is assigned to a single cluster)
Page 42

43. Rajarshi Dutta
Rather than defining groups before looking at the data, clustering allows you to find and
analyze the groups that have formed organically. The "Choosing K" section below describes
how the number of groups can be determined.
Each centroid of a cluster is a collection of feature values which define the resulting groups.
Examining the centroid feature weights can be used to qualitatively interpret what kind of
group each cluster represents.
The K-means clustering algorithm is used to find groups which have not been explicitly
labeled in the data. This can be used to confirm business assumptions about what types of
groups exist or to identify unknown groups in complex data sets. Once the algorithm has
been run and the groups are defined, any new data can be easily assigned to the correct
group.
This is a versatile algorithm that can be used for any type of grouping. Some examples of use
cases are:
Behavioral segmentation:
• Segment by purchase history
• Segment by activities on application, website, or platform
• Define personas based on interests
• Create profiles based on activity monitoring
Inventory categorization:
• Group inventory by sales activity
• Group inventory by manufacturing metrics
Sorting sensor measurements:
• Detect activity types in motion sensors
• Group images
• Separate audio
• Identify groups in health monitoring
Detecting bots or anomalies:
• Separate valid activity groups from bots
Page 43

44. Rajarshi Dutta
• Group valid activity to clean up outlier detection
To perform K-means clustering, we must first specify the desired number of clusters K; then
the K-means algorithm will assign each observation to exactly one of the K clusters.
1. Randomly assign a number, from 1 to K, to each of the observations. These serve as initial
cluster assignments for the observations.
2. Iterate until the cluster assignments stop changing:
. (a) For each of the K clusters, compute the cluster centroid. The kth cluster
centroid is the vector of the p feature means for the observations in the kth cluster.
. (b) Assign each observation to the cluster whose centroid is closest (where
closest is defined using Euclidean distance).
Page 44

45. Rajarshi Dutta
Page 45

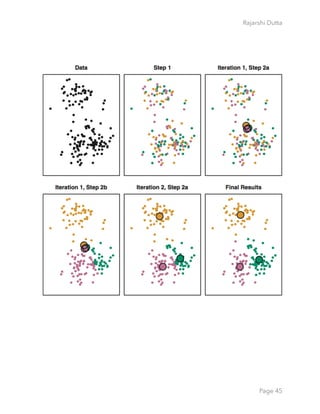
46. Rajarshi Dutta
data <-read.csv("Wholesale customers data.csv",header=T) ## Download
the data from https://archive.ics.uci.edu/ml/datasets/Wholesale
+customers
summary(data)
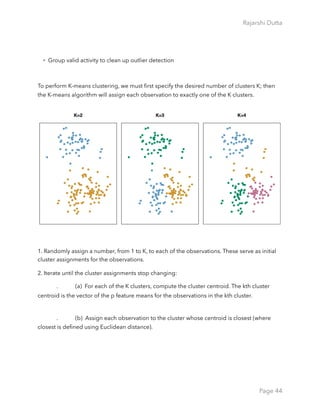
There’s obviously a big difference for the top customers in each category (e.g. Fresh goes
from a min of 3 to a max of 112,151). Normalizing / scaling the data won’t necessarily remove
those outliers. Doing a log transformation might help. We could also remove those
customers completely. From a business perspective, you don’t really need a clustering
algorithm to identify what your top customers are buying. You usually need clustering and
segmentation for your middle 50%.
With that being said, let’s try removing the top 5 customers from each category. We’ll use a
custom function and create a new data set called data.rm.top
top.n.custs <- function (data,cols,n=5) { #Requires some data frame
and the top N to remove
idx.to.remove <-integer(0) #Initialize a vector to hold customers
being removed
for (c in cols){ # For every column in the data we passed to this
function
col.order <-order(data[,c],decreasing=T) #Sort column "c" in
descending order (bigger on top)
#Order returns the sorted index (e.g. row 15, 3, 7, 1, ...) rather
than the actual values sorted.
Page 46

47. Rajarshi Dutta
idx <-head(col.order, n) #Take the first n of the sorted column C
to
idx.to.remove <-union(idx.to.remove,idx) #Combine and de-duplicate
the row ids that need to be removed
}
return(idx.to.remove) #Return the indexes of customers to be removed
}
top.custs <-top.n.custs(data,cols=3:8,n=5)
length(top.custs) #How Many Customers to be Removed?
data[top.custs,] #Examine the customers
data.rm.top<-data[-c(top.custs),] #Remove the Customers
summary(data.rm.top) ## removed the top customers
set.seed(76964057) #Set the seed for reproducibility
#Create 5 clusters, Remove columns 1 and 2
k <-kmeans(data.rm.top[,-c(1,2)], centers=5)
k$centers #Display&nbsp;cluster centers
Page 47

48. Rajarshi Dutta
table(k$cluster) #Give a count of data points in each cluster
Cluster 1 looks to be a heavy Grocery and above average Detergents_Paper but low Fresh
foods.
Cluster 3 is dominant in the Fresh category.
Cluster 5 might be either the “junk drawer” catch-all cluster or it might represent the small
customers.
A measurement that is more relative would be the withinss and betweenss.
• k$withinss would tell you the sum of the square of the distance from each data point to the
cluster center. Lower is better. Seeing a high withinss would indicate either outliers are in
your data or you need to create more clusters.
• k$betweenss tells you the sum of the squared distance between cluster centers. Ideally you
want cluster centers far apart from each other.
It’s important to try other values for K. You can then compare withinss and betweenss. This
will help you select the best K. For example, with this data set, what if you ran K from 2
through 20 and plotted the total within sum of squares? You should find an “Elbow” point.
Wherever the graph bends and stops making gains in withinss you call that your K.
rng<-2:20 #K from 2 to 20
tries <-100 #Run the K Means algorithm 100 times
avg.totw.ss <-integer(length(rng)) #Set up an empty vector to hold all
of points
for(v in rng){ # For each value of the range variable
v.totw.ss <-integer(tries) #Set up an empty vector to hold the 100
tries
for(i in 1:tries){
Page 48

49. Rajarshi Dutta
k.temp <-kmeans(data.rm.top,centers=v) #Run kmeans
v.totw.ss[i] <-k.temp$tot.withinss#Store the total withinss
}
avg.totw.ss[v-1] <-mean(v.totw.ss) #Average the 100 total withinss
}
plot(rng,avg.totw.ss,type="b", main="Total Within SS by Various K",
ylab="Average Total Within Sum of Squares",
xlab="Value of K")
Page 49

50. Rajarshi Dutta
This plot doesn’t show a very strong elbow. Somewhere around K = 5 we start losing
dramatic gains. So for now we are satisfied with 5 clusters.
‘Artificial’ Neural Network
A typical artificial neural network has anything from a few dozen to hundreds, thousands, or
even millions of artificial neurons called units arranged in a series of layers, each of which
connects to the layers on either side. Some of them, known as input units, are designed to
receive various forms of information from the outside world that the network will attempt to
learn about, recognize, or otherwise process. Other units sit on the opposite side of the
network and signal how it responds to the information it's learned; those are known as output
Page 50

51. Rajarshi Dutta
units. In between the input units and output units are one or more layers of hidden units,
which, together, form the majority of the artificial brain. Most neural networks are fully
connected, which means each hidden unit and each output unit is connected to every unit in
the layers either side. The connections between one unit and another are represented by a
number called a weight, which can be either positive (if one unit excites another) or negative
(if one unit suppresses or inhibits another). The higher the weight, the more influence one
unit has on another. (This corresponds to the way actual brain cells trigger one another across
tiny gaps called synapses.)
Page 51

52. Rajarshi Dutta
One should be able to tell that it is a giraffe, despite it being strangely
fat. We recognize images and objects instantly, even if these images are
presented in a form that is different from what we have seen before. We
do this with the 80 billion neurons in our brain working together to
transmit information. This remarkable system of neurons is also the
inspiration behind a widely-used machine learning technique called
Artificial Neural Networks (ANN). Some computers using this technique
have even out-performed humans in recognizing images.
Image recognition is important for many of the advanced technologies we use today. It is
used in visual surveillance, guiding autonomous vehicles and even identifying ailments from
X-ray images. Most modern smartphones also come with image recognition apps that convert
handwriting into typed words.
In this section we will look at how we can train an ANN algorithm to recognize images of
handwritten digits. We will be using the images from the famous MNIST (Mixed National
Institute of Standards and Technology) database.
Page 52

53. Rajarshi Dutta
Out of the 1,000 handwritten images that the model was asked to recognize, it correctly
identified 922 of them, which is a 92.2% accuracy. We can use a contingency table to view the
results, as shown below:
From the table, we can see that when given a handwritten image of either “0” or “1”, the
model almost always identifies it correctly. On the other hand, the digit “5” is the trickiest to
identify. An advantage of using a contingency table is that it tells us the frequency of mis-
identification. Image of the digit “2” are misidentified as “7” or “8” about 8% of the time.
How The Model Works
Step 1. When the input node is given an image, it activates a unique set of neurons in the first
layer, starting a chain reaction that would pave a unique path to the output node. In Scenario
1, neurons A, B, and D are activated in layer 1.
Step 2. The activated neurons send signals to every connected neuron in the next layer. This
directly affects which neurons are activated in the next layer. In Scenario 1, neuron A sends a
signal to E and G, neuron B sends a signal to E, and neuron D sends a signal to F and G.
Page 53

54. Rajarshi Dutta
Step 3. In the next layer, each neuron is governed by a rule on what combinations of received
signals would activate the neuron. In Scenario 1, neuron E is activated by the signals from A
and B. However, for neuron F and G, their neurons’ rules tell them that they have not received
the right signals to be activated, and hence they remain grey.
Step 4. Steps 2-3 are repeated for all the remaining layers (it is possible for the model to have
more than 2 layers), until we are left with the output node.
Step 5. The output node deduces the correct digit based on signals received from neurons in
the layer directly preceding it (layer 2). Each combination of activated neurons in layer 2 leads
to one solution, though each solution can be represented by different combinations of
activated neurons. In Scenarios 1 & 2, two images are fed as input. Because the images are
Page 54

55. Rajarshi Dutta
different, the network activates different neural paths from input to the output. However, the
output is still recognizes both images as the digit “6”.
We are going to use the Boston dataset in the MASS package.
The Boston dataset is a collection of data about housing values in the suburbs of Boston. Our
goal is to predict the median value of owner-occupied homes (medv) using all the other
continuous variables available.
set.seed(500)
library(MASS)
library(neuralnet)
data <- Boston
index <- sample(1:nrow(data),round(0.75*nrow(data)))
train <- data[index,]
test <- data[-index,]
maxs <- apply(data, 2, max)
mins <- apply(data, 2, min)
#It is good practice to normalize your data before training a neural
#network. I cannot emphasize enough how important this step is:
#depending on your dataset, avoiding normalization may lead to useless
#results or to a very difficult training process (most of the times
#the algorithm will not converge before the number of maximum
#iterations allowed). You can choose different methods to scale the
#data (z-normalization, min-max scale, etc…). I chose to use the min-
#max method and scale the data in the interval [0,1]. Usually scaling
#in the intervals [0,1] or [-1,1] tends to give better results.
scaled <- as.data.frame(scale(data, center = mins, scale = maxs -
mins)) ## Neural
train_ <- scaled[index,]
test_ <- scaled[-index,]
n <- names(train_)
Page 55

56. Rajarshi Dutta
f <- as.formula(paste("medv ~", paste(n[!n %in% "medv"], collapse = "
+ ")))
nn <- neuralnet(f,data=train_,hidden=c(5,3),linear.output=T)
plot(nn)
pr.nn <- compute(nn,test_[,1:13])
pr.nn_ <- pr.nn$net.result*(max(data$medv)-min(data$medv))+min(data
$medv)
test.r <- (test_$medv)*(max(data$medv)-min(data$medv))+min(data$medv)
Page 56

57. Rajarshi Dutta
Summary
In this article I just covered a very small set of algorithms from a very large universe of the
models. The idea was to create pointers to step in this domain, I guess you can now have the
head start of this field. To summarize I would like to touch upon some comparative analysis
between the algorithms we just discussed in this section.
When it comes to choosing the right algorithm for the problem, there are number of factors
based on we can decide which one to choose.
‣ Number of training examples
‣ Dimensionality of the feature space
‣ Do I expect the problem to be linearly separable?
‣ Are features independent?
‣ Are features expected to linearly dependent with the target variable? Is overfitting
expected to be a problem?
‣ What are the system's requirement in terms of speed/performance/memory usage?
Page 57

58. Rajarshi Dutta
Linear Regression
Advantages
‣ Very simple algorithm
‣ Doesn’t take a lot of memory
‣ Quite fast
‣ Easy to explain
Disadvantages
‣ requires the data to be linearly spread
‣ is unstable in case features are redundant, i.e if there is multicollinearity
Decision Tree
Advantages
‣ quite simple
‣ easy to communicate about
‣ easy to maintain
‣ few parameters are required and they are quite intuitive
‣ prediction is quite fast
Page 58

59. Rajarshi Dutta
Disadvantages
‣ can take a lot of memory (the more features you have, the deeper and larger your decision
tree is likely to be)
‣ naturally overfits a lot (it generates high-variance models, it suffers less from that if the
branches are pruned, though)
‣ not capable of being incrementally improved
Random Forest
Advantages
‣ is robust to overfitting (thus solving one of the biggest disadvantages of decision trees)
‣ parameterization remains quite simple and intuitive
‣ performs very well when the number of features is big and for large quantity of learning
data
Disadvantages
‣ models generated with Random Forest may take a lot of memory
‣ learning may be slow (depending on the parameterization)
‣ not possible to iteratively improve the generated models
Page 59

60. Rajarshi Dutta
Logistics Regression
Advantages
‣ Simple to understand and explain
‣ It seldom overfits
‣ Using L1 & L2 regularization is effective in feature selection
‣ The best algorithm for predicting probabilities of an event
‣ Fast to train
‣ Easy to train on big data thanks to its stochastic version
Disadvantages
‣ You have to work hard to make it fit nonlinear functions
‣ Can suffer from outliers
Support Vector Machine
Advantages
‣ is mathematically designed to reduce the overfitting by maximizing the margin between
data points
‣ prediction is fast
‣ Does not care about the outliers
‣ can manage a lot of data and a lot of features (high dimensional problems)
Page 60

61. Rajarshi Dutta
‣ doesn’t take too much memory to store
Disadvantages
‣ can be time consuming to train
‣ parameterization can be tricky in some cases
‣ communicating isn’t easy
Artificial Neural Network
Advantages
‣ very complex models can be trained
‣ can be used as a kind of black box, without performing a complex feature engineering
before training the model
‣ numerous kinds of network structures can be used, allowing you to enjoy very interesting
properties (CNN, RNN, LSTM, etc.). Combined with the “deep approach” even more
complex models can be learned unleashing new possibilities: object recognition has been
recently greatly improved using Deep Neural Networks.
Disadvantages
‣ very hard to simply explain (people usually say that a Neural Network behaves and learns
like a little human brain)
‣ parameterization is very complex (what kind of network structure should you choose? What
are the best activation functions for my problem?)
‣ requires a lot more learning data than usual
‣ final model may takes a lot of memory
Page 61

62. Rajarshi Dutta
K-Means Clustering
Advantages
‣ parametrization is intuitive and works well with a lot of data
Disadvantages
‣ needs to know in advance how many clusters there will be in your data … This may require
a lot of trials to “guess” the best K number of clusters to define.
‣ Clustering may be different from one run to another due to the random initialization of the
algorithm
Advantage or drawback:
The K-Means algorithm is actually more a partitioning algorithm than a clustering algorithm. It
means that, if there is noise in your unlabelled data, it will be incorporated within your final
clusters.
Page 62

63. Rajarshi Dutta
Summary Table
Page 63

64. Rajarshi Dutta
References
Web Reference:
http://machinelearningmastery.com/
http://wikipedia.com
https://www.r-bloggers.com
https://datasciencemadesimpler.wordpress.com
https://datascienceplus.com/
http://blog.kaggle.com
https://www.analyticsvidhya.com
https://en.wikipedia.org/
http://bigdata-madesimple.com/
http://www.learnbymarketing.com/
https://algobeans.com
Book:
An Introduction to statistical learning
Page 64