This document discusses machine learning and deep learning techniques. It begins with an overview of self-taught learning and testing unlabeled images. It then discusses biology aspects of neural networks and experiments with brain ports. The remainder of the document focuses on deep learning algorithms including deep belief networks, deep sparse autoencoders, deep convolution neural networks, and residual networks. It also discusses using autoencoders for unsupervised feature learning and greedy learning approaches. Finally, it provides an overview of convolution neural networks including their use in visual processing and image representation.

1. Machine Learning
Deep Learning
Inas A. Yassine
Systems and Biomedical Engineering Department,
Faculty of Engineering - Cairo University
iyassine@eng.cu.edu.eg

2. Self-taught learning
Testing:
What is this?
Car Motorcycle
Unlabeled images (random internet images)

3. Deep Learning
§ Biology Aspect
§ Each neuron is fired due to a certain edge
direction
§ New Wiring Experiment
§ Brain port
§ Automate what we see as a face….

4. Self-taught learning
Sparse
coding,
LCC, etc.
f1, f2, …, fk
Car Motorcycle
Use learned f1, f2, …, fk to represent training/test sets.
Using f1, f2, …, fk
a1, a2, …, ak
If have labeled training
set is small, can give
huge performance
boost.

5. Learning feature
hierarchies/Deep learning

6. Why feature hierarchies
pixels edges object parts
(combination
of edges)
Convolution batches !

7. Deep learning algorithms
§ Stack sparse coding algorithm
§ Deep Belief Network (DBN) (Hinton)
§ Deep sparse autoencoders (Bengio)
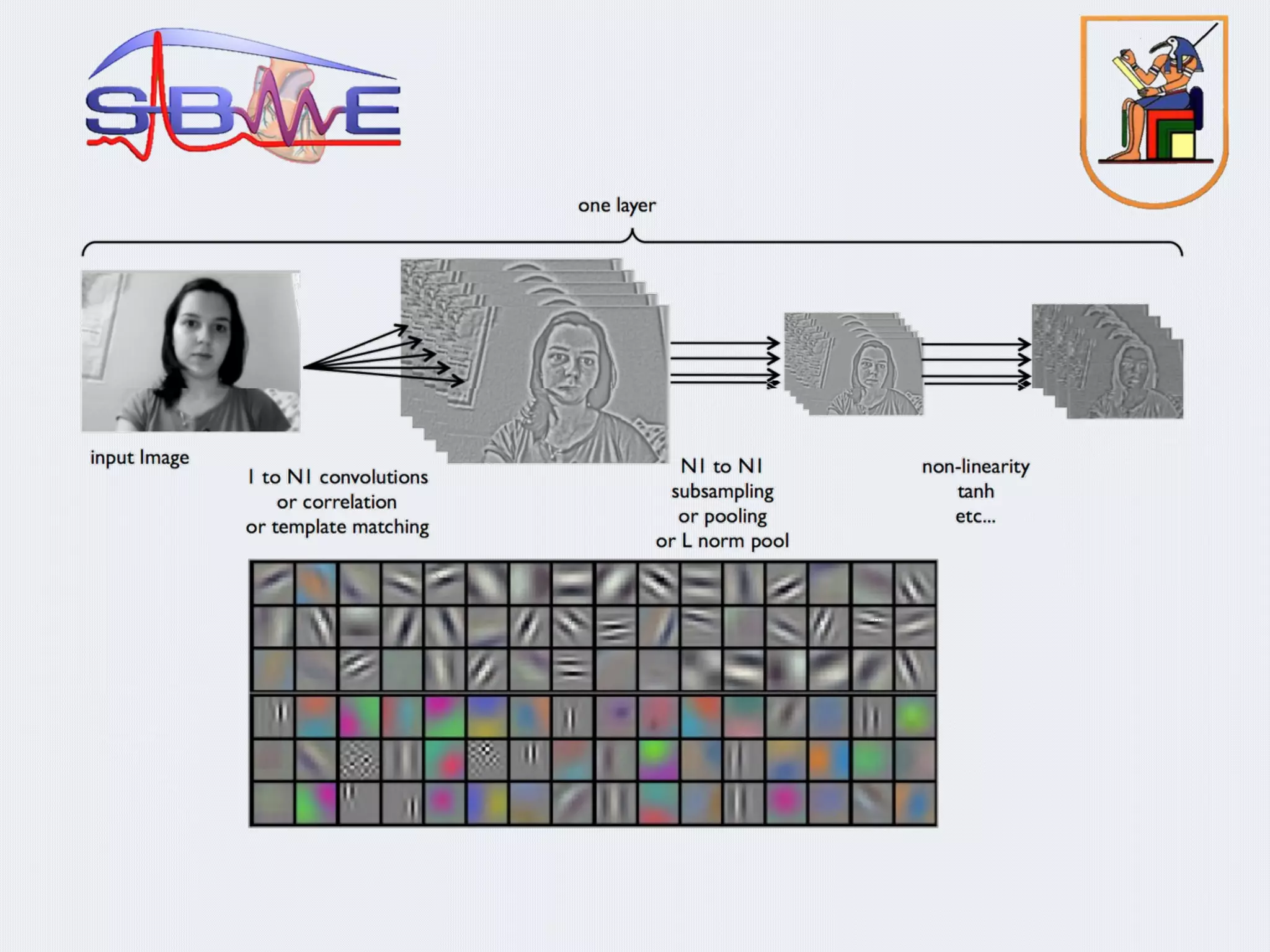
§ Deep Convolution Neural Networks
§ Residual Networks
§ Seams Networks
§ Self Learning Netowrks
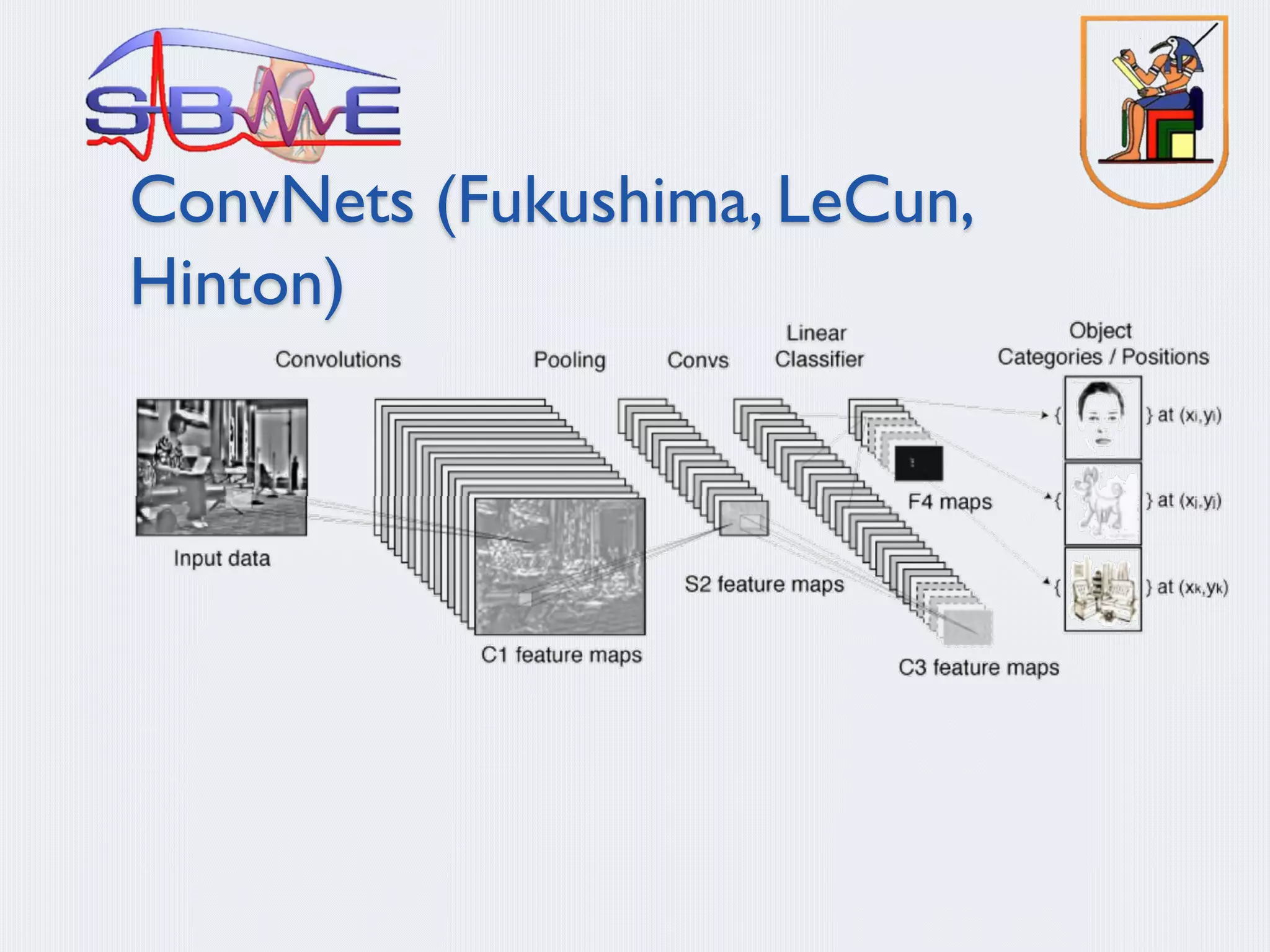
[Other related work: LeCun, Lee,Yuille, Ng …]

8. Deep Learning:Autoencoder

9. Deep learning with autoencoders
§ Logistic regression
§ Neural network
§ Sparse autoencoder
§ Deep autoencoder

10. Logistic regression has a learned parameter vector q.
On input x, it outputs:
where
Logistic regression
x1
x2
x3
+1
Draw a logistic
regression unit as:

11. Neural Network
String a lot of logistic units together. Example 3 layer network:
x1
x2
x3
+1 +1
a3
a2
a1
Layer 1 Layer 2
Layer 3

12. Neural Network
x1
x2
x3
+1 +1
Layer 1 Layer 2
Layer 4+1
Layer 3
Example” 4 layer network with 2 output units:

13. Training a neural network
Given training set (x1, y1), (x2, y2), (x3, y3 ), ….
Adjust parameters q (for every node) to make:
(Use gradient descent.“Backpropagation” algorithm. Susceptible to local optima.)

14. Unsupervised feature learning
x4
x5
x6
+1
Layer 1
Layer 2
x1
x2
x3
x4
x5
x6
x1
x2
x3
+1
Layer 3
Network is trained to
output the input (learn
identify function).
Minimizing both information
of data and output
Trivial solution unless:
- Constrain number of units
in Layer 2 (learn compressed
representation), or
- Constrain Layer 2 to be
sparse.
a1
a2
a3

15. Training a sparse autoencoder.
Given unlabeled training set x1, x2,
Unsupervised feature learning with ANN
Reconstruction error
term
𝑊" 𝑊X
a1
a2
a3

16. Unsupervised feature learning with ANN
x4
x5
x6
+1
Layer 1
Layer 2
x1
x2
x3
x4
x5
x6
x1
x2
x3
+1
Layer 3

17. Unsupervised feature learning with ANN
New representation for input.
x4
x5
x6
+1
Layer 1
Layer 2
x1
x2
x3
+1

18. Unsupervised feature learning with ANN
x4
x5
x6
+1
Layer 1
Layer 2
x1
x2
x3
+1
+1
b1
b2
b3
Train parameters so that ,
subject to bi’s being sparse.

19. Greedy Learning
Regularization
using back
propagation of
the complete
system after
greedy + 5%
increase in
performance
x4
x5
x6
+1
Layer 1
Layer 2
x1
x2
x3
+1+1
b1
b2
b3
x4
x5
x6
+1
Layer 1
Layer 2
x1
x2
x3
+1

20. Sparse Autoencoder

21. First stage of visual processing in
brain:V1
Schematic of simple cell Actual simple cell
“Gabor functions.”
The first stage of
visual processing in
the brain (V1) does
“edge detection.”

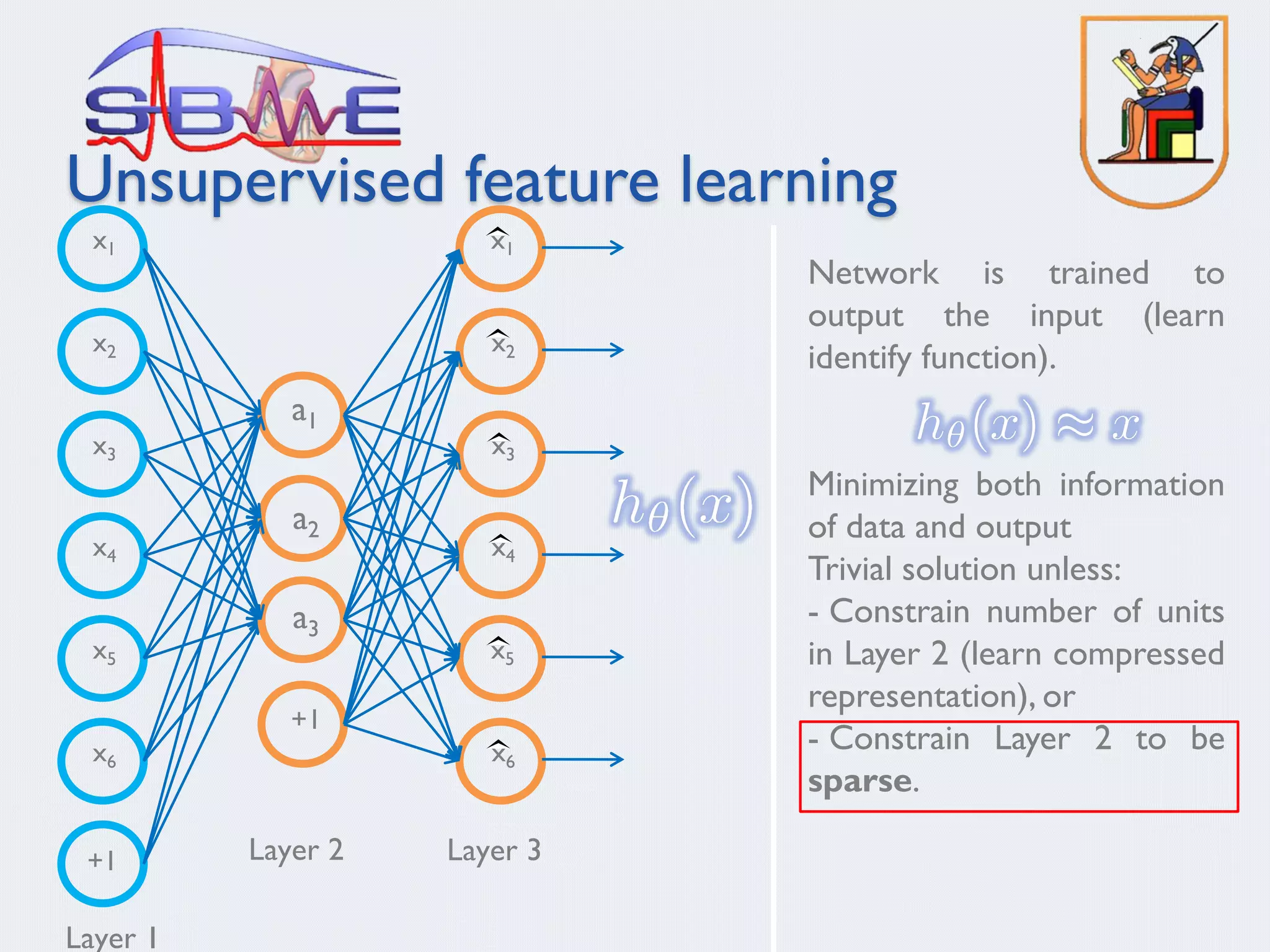
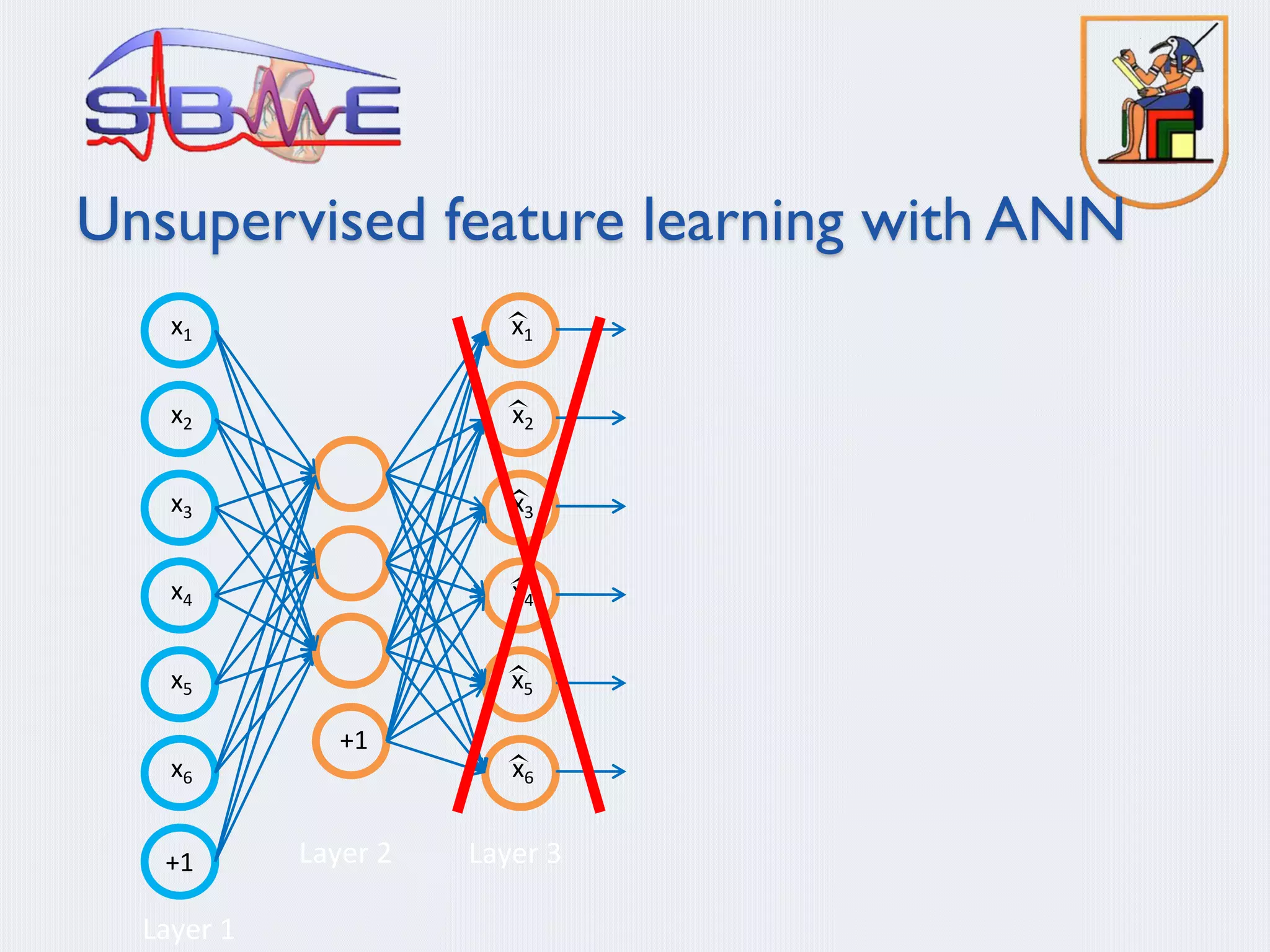
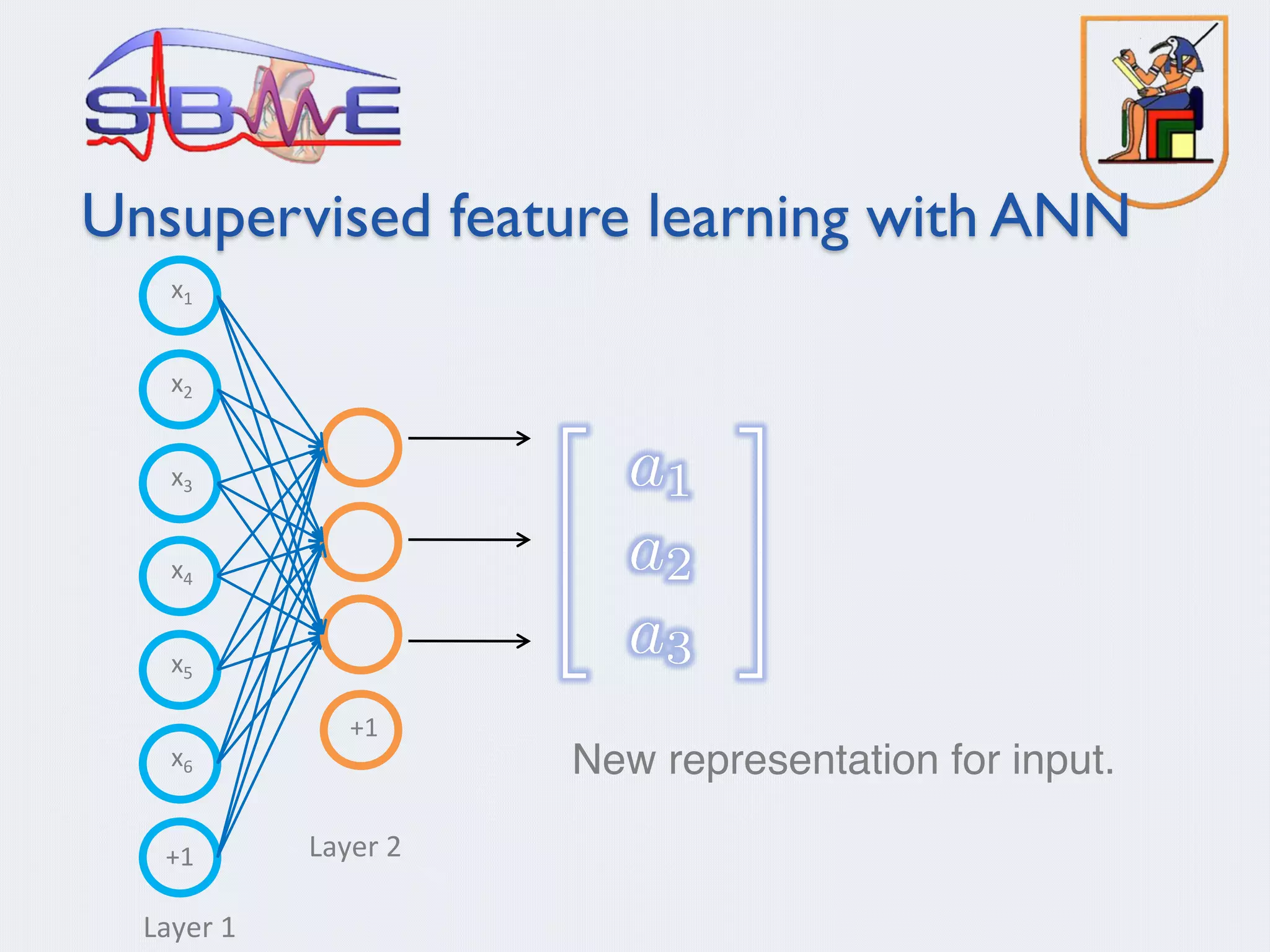
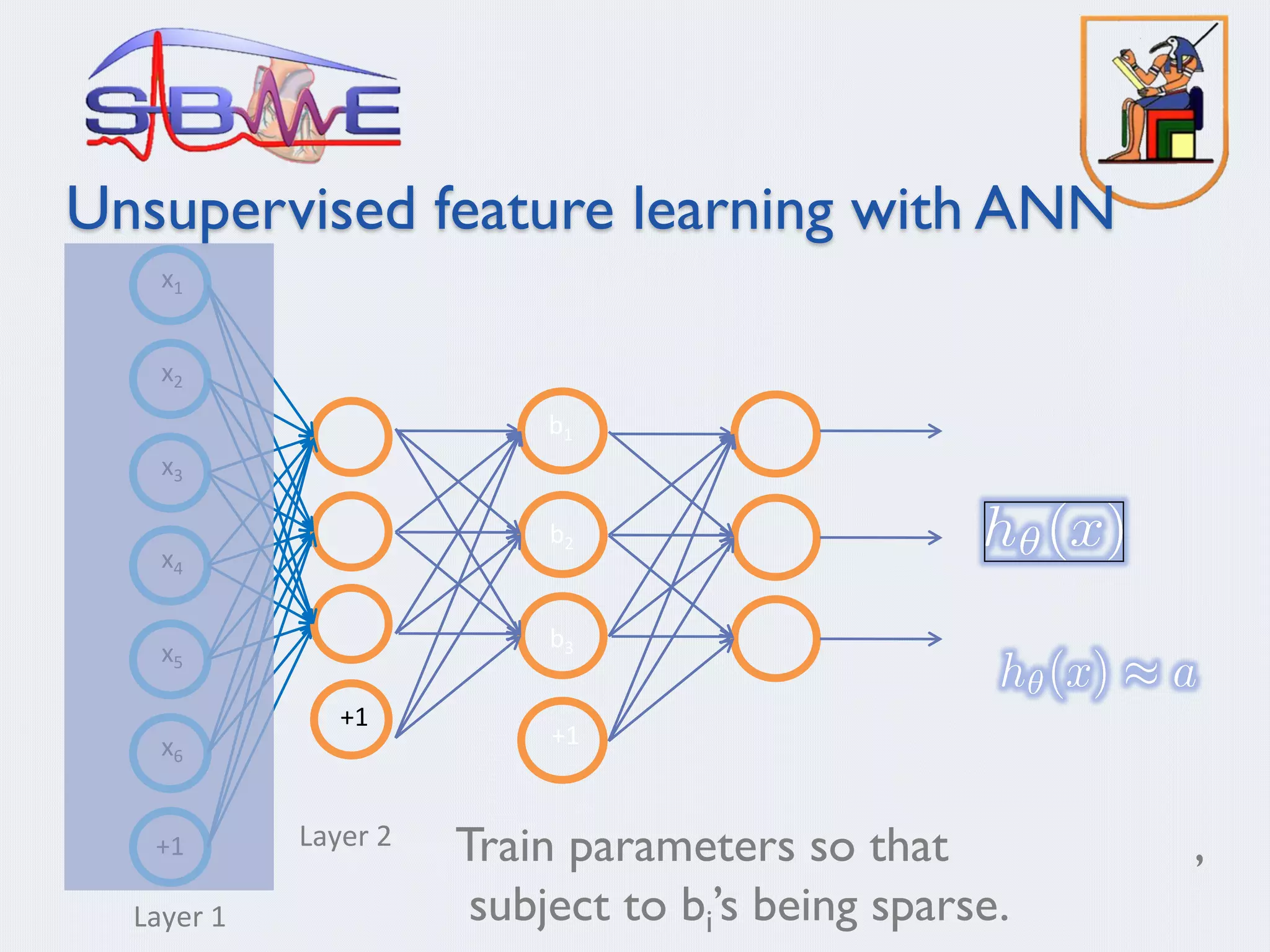
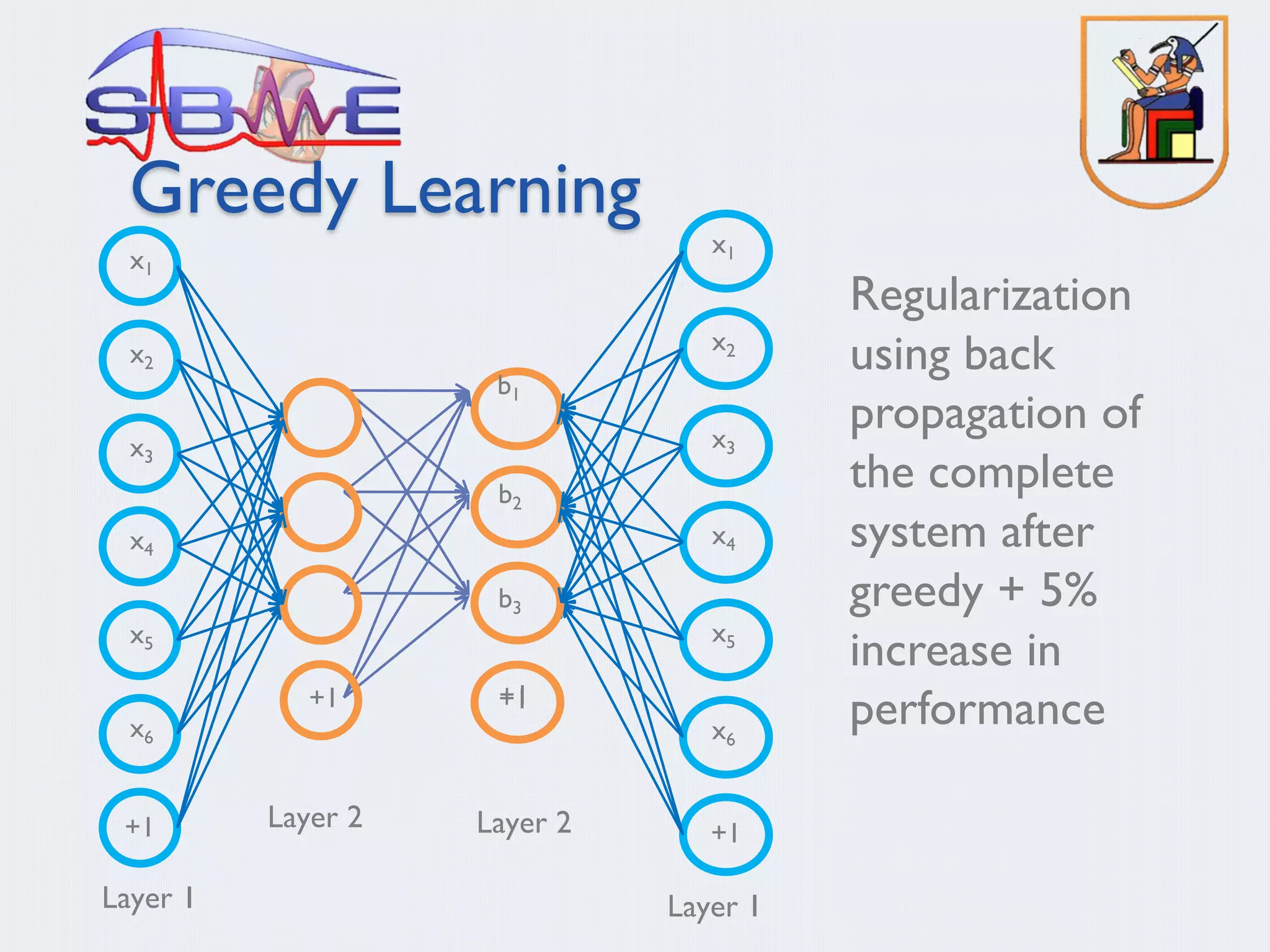
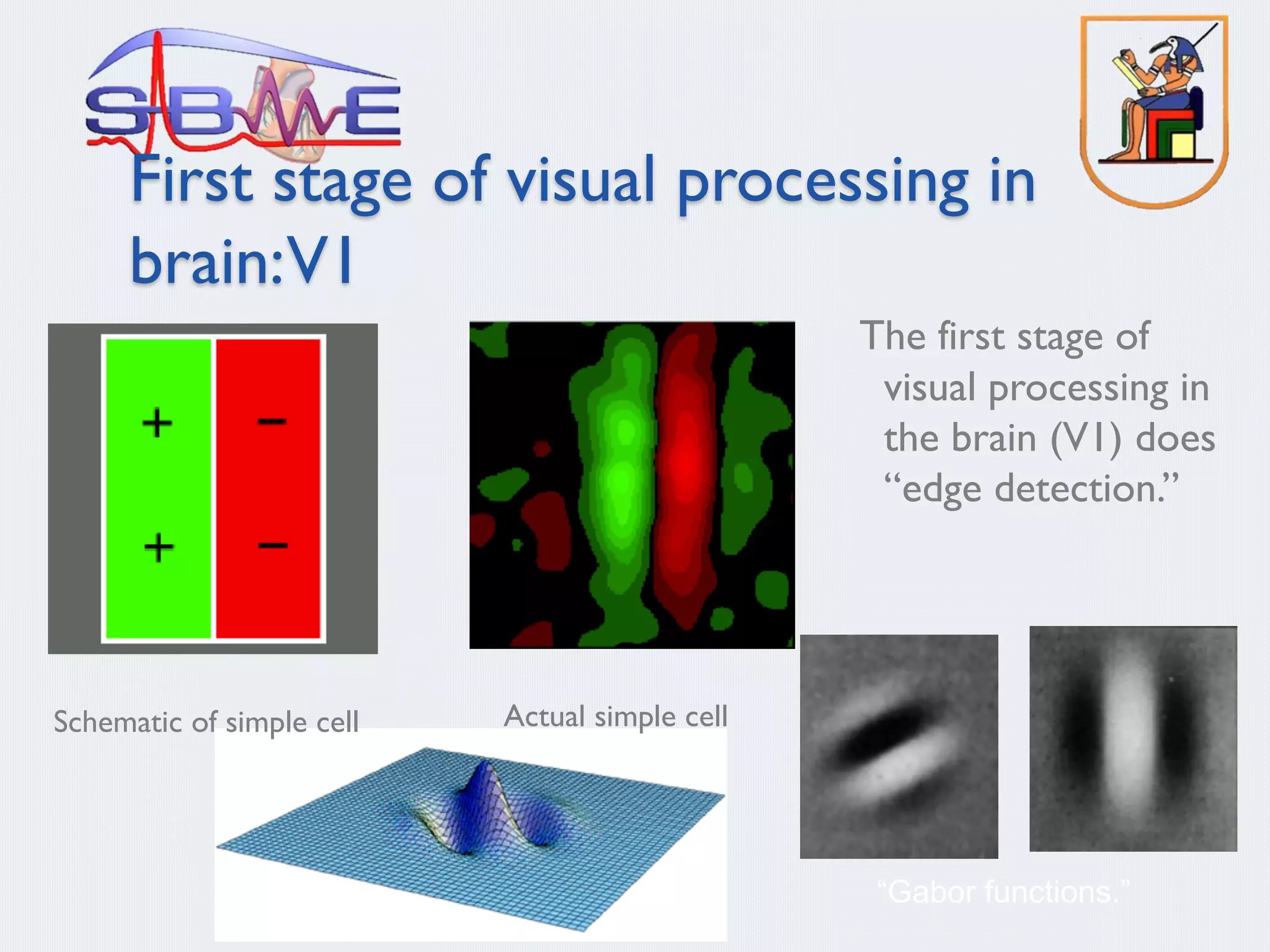
22. Learning an image representation
Sparse coding (Olshausen & Field,1996)
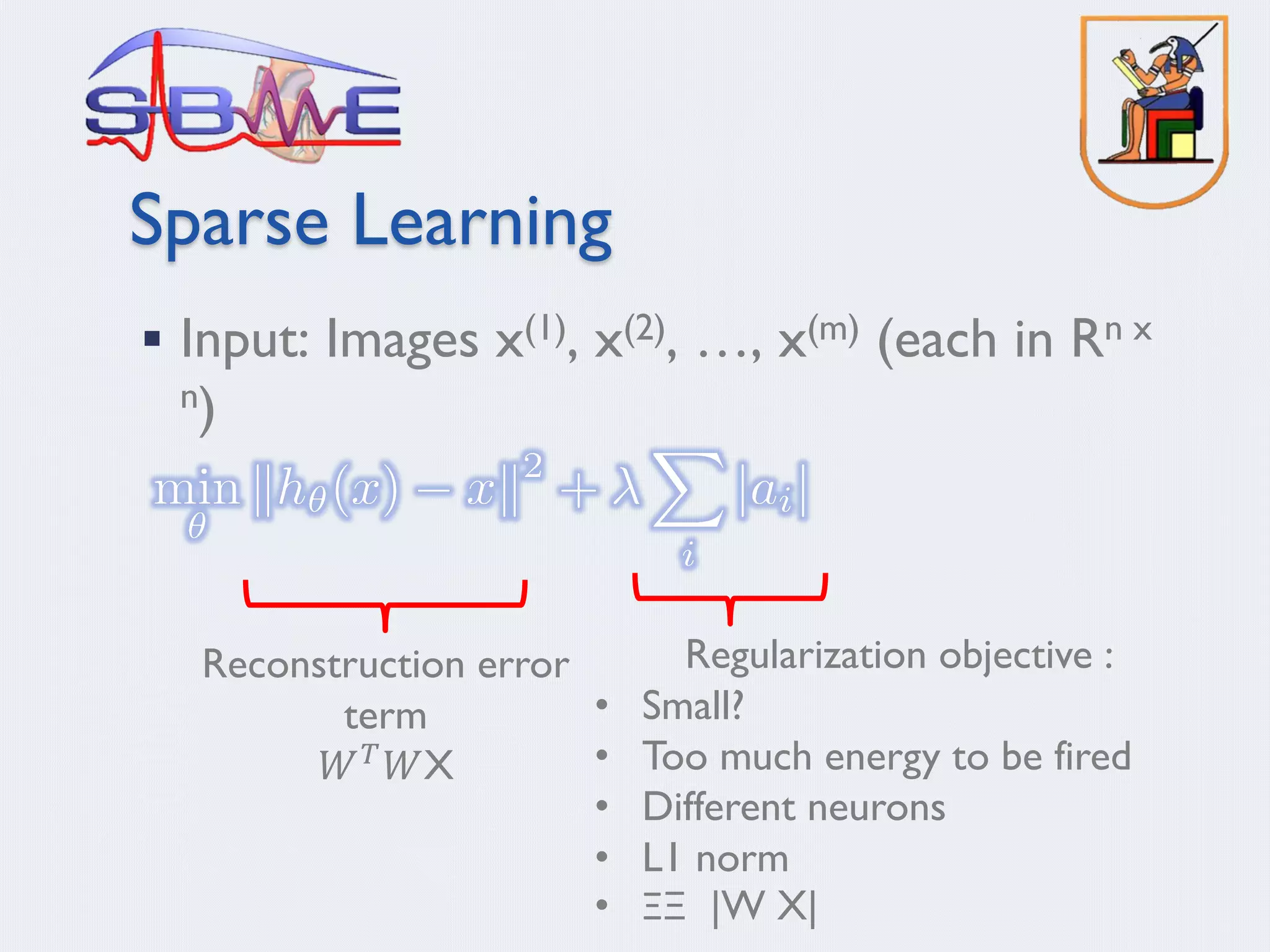
Input: Images x(1), x(2), …, x(m) (each in Rn x n)
Learn: Dictionary of bases f1, f2, …, fk (also Rn x n), so that each
input x can be approximately decomposed as:
s.t. aj’s are mostly zero (“sparse”)
Use to represent 14x14 image patch succinctly, as [a7=0.8, a36=0.3,
a41 = 0.5]. I.e., this indicates which “basic edges” make up the
image.

23. Sparse coding illustration
Natural Images
Learned bases (f1 , …, f64): “Edges”
50 100 150 200 250 300 350 400 450 500
50
100
150
200
250
300
350
400
450
500
50 100 150 200 250 300 350 400 450 500
50
100
150
200
250
300
350
400
450
500
50 100 150 200 250 300 350 400 450 500
50
100
150
200
250
300
350
400
450
500
» 0.8 * + 0.3 * + 0.5 *
x » 0.8 * f36
+ 0.3 * f42 + 0.5 * f63
[0, 0, …, 0, 0.8, 0, …, 0, 0.3, 0, …, 0, 0.5, …]
Test example

24. Represent as: [0, 0, …, 0, 0.6, 0, …, 0, 0.8, 0, …, 0, 0.4, …]
Represent as: [0, 0, …, 0, 1.3, 0, …, 0, 0.9, 0, …, 0, 0.3, …]
More examples
» 0.6 * + 0.8 * + 0.4 *
f15 f28
f37
» 1.3 * + 0.9 * + 0.3 *
f5 f18
f29
• Method hypothesizes that edge-like patches are the most
“basic” elements of a scene, and represents an image in terms of
the edges that appear in it.
• Use to obtain a more compact, higher-level representation of
the scene than pixels.

25. Sparse Learning
§ Input: Images x(1), x(2), …, x(m) (each in Rn x
n)
Reconstruction error
term
𝑊" 𝑊X
Regularization objective :
• Small?
• Too much energy to be fired
• Different neurons
• L1 norm
• ΞΞ |W X|

26. DEEP LEARNING:
CONVOLUTION NEURAL
NETWORK

27. ConvNets (Fukushima, LeCun,
Hinton)

28. ConvNets

30. Convolution
§ Correlation
§ Convolution

31. Image Convolution

33. Image Convolution

34. Image Convolution

35. Image Convolution

36. ConvNets in Torch