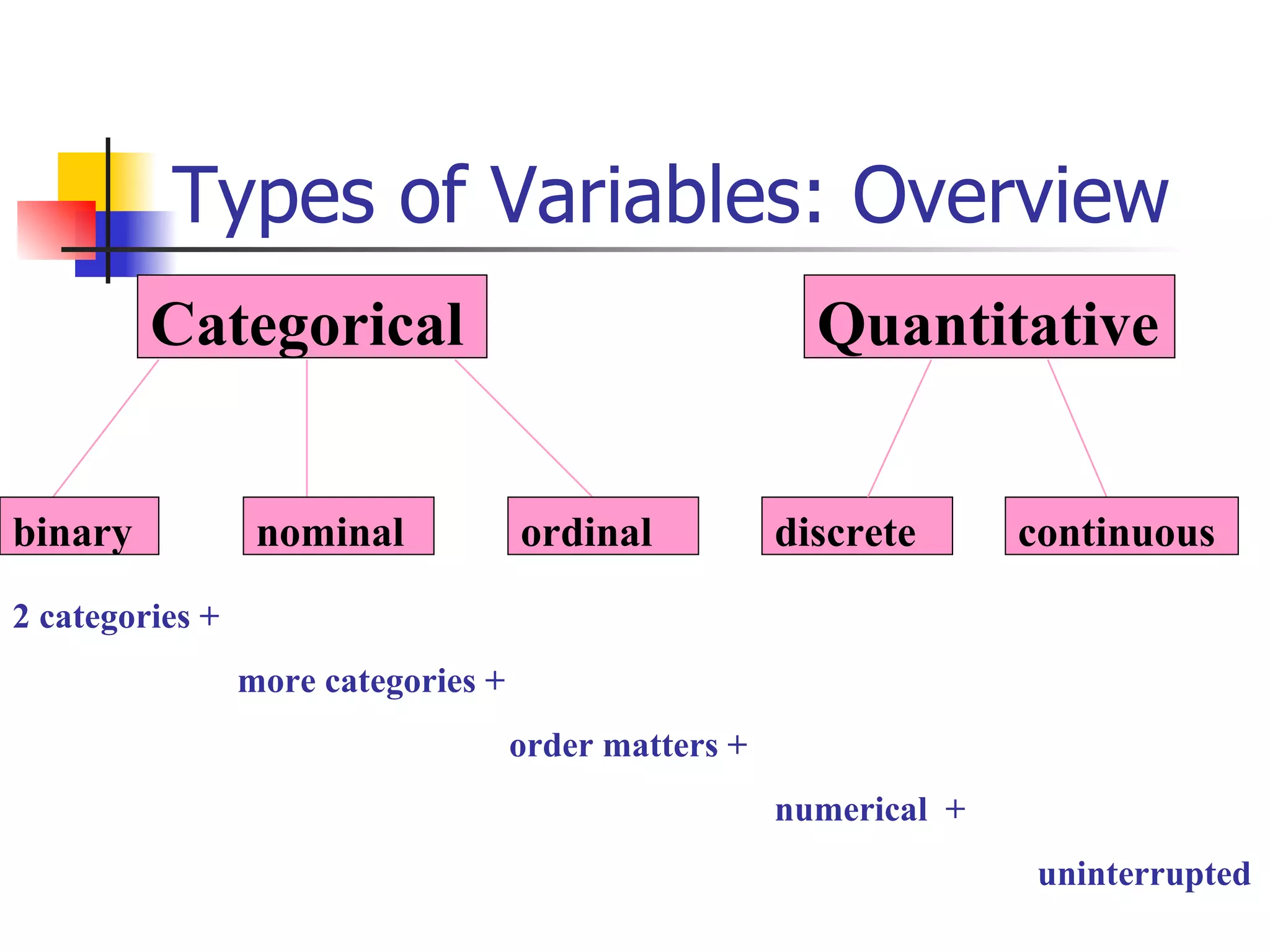
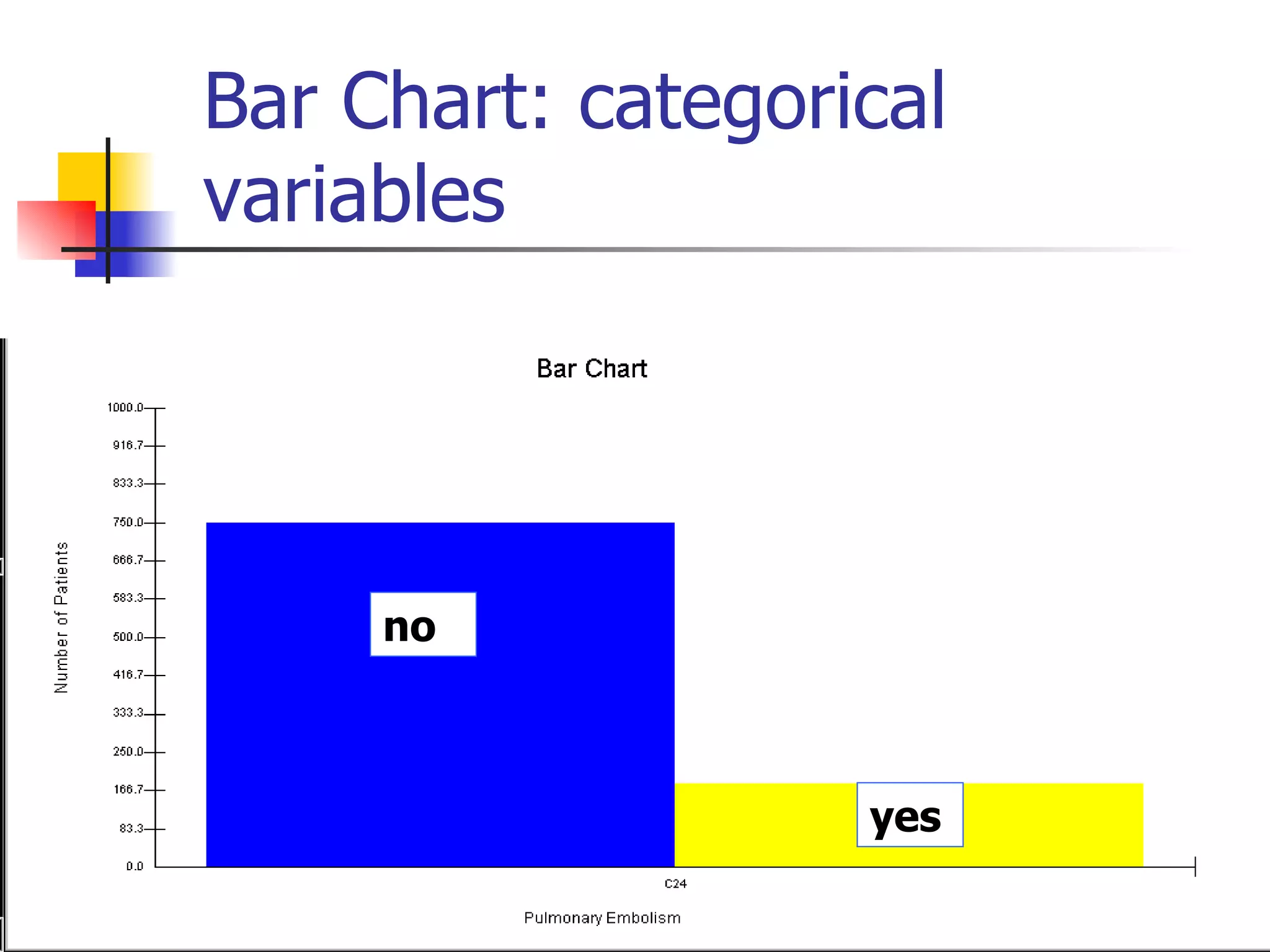
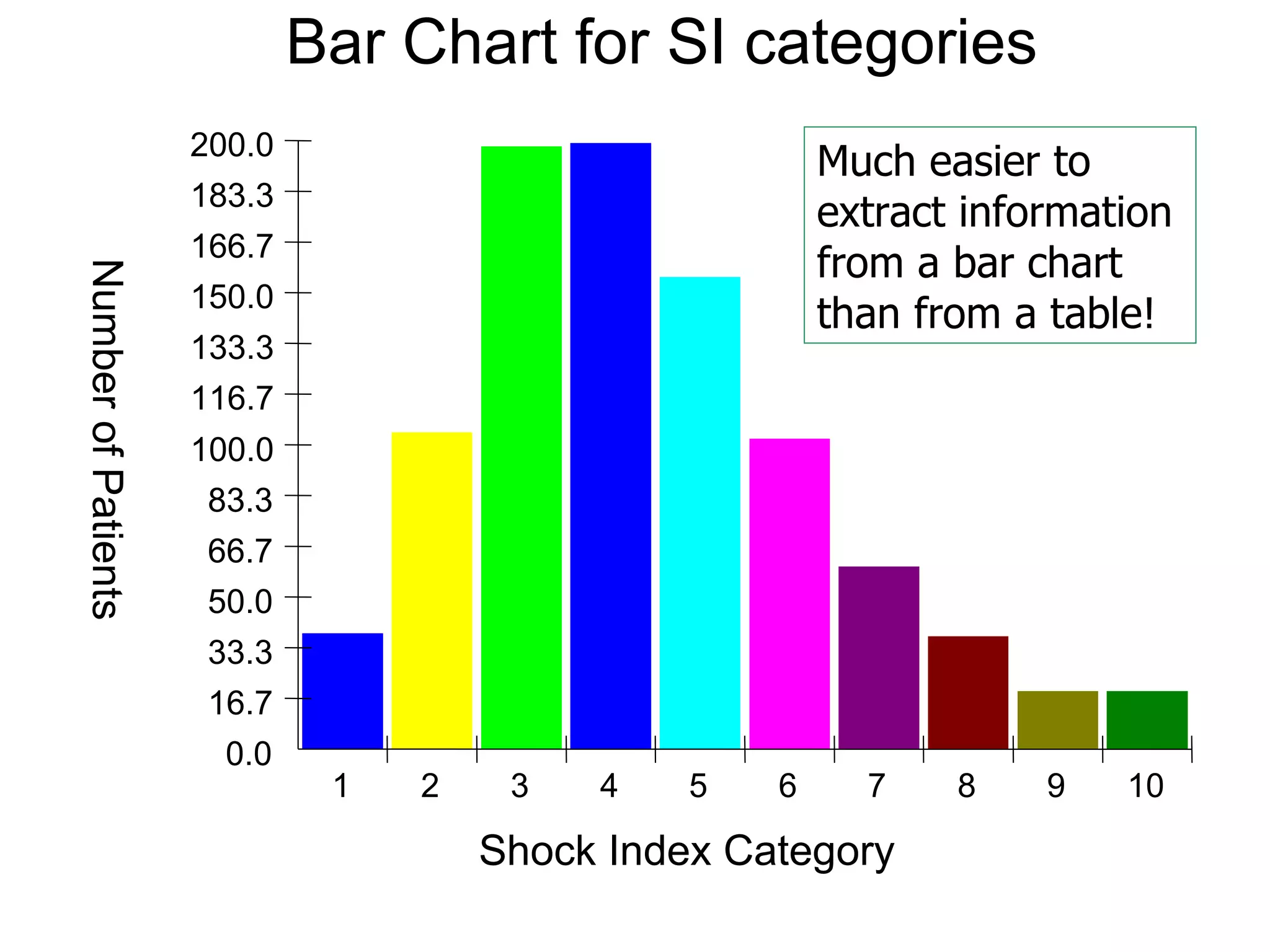
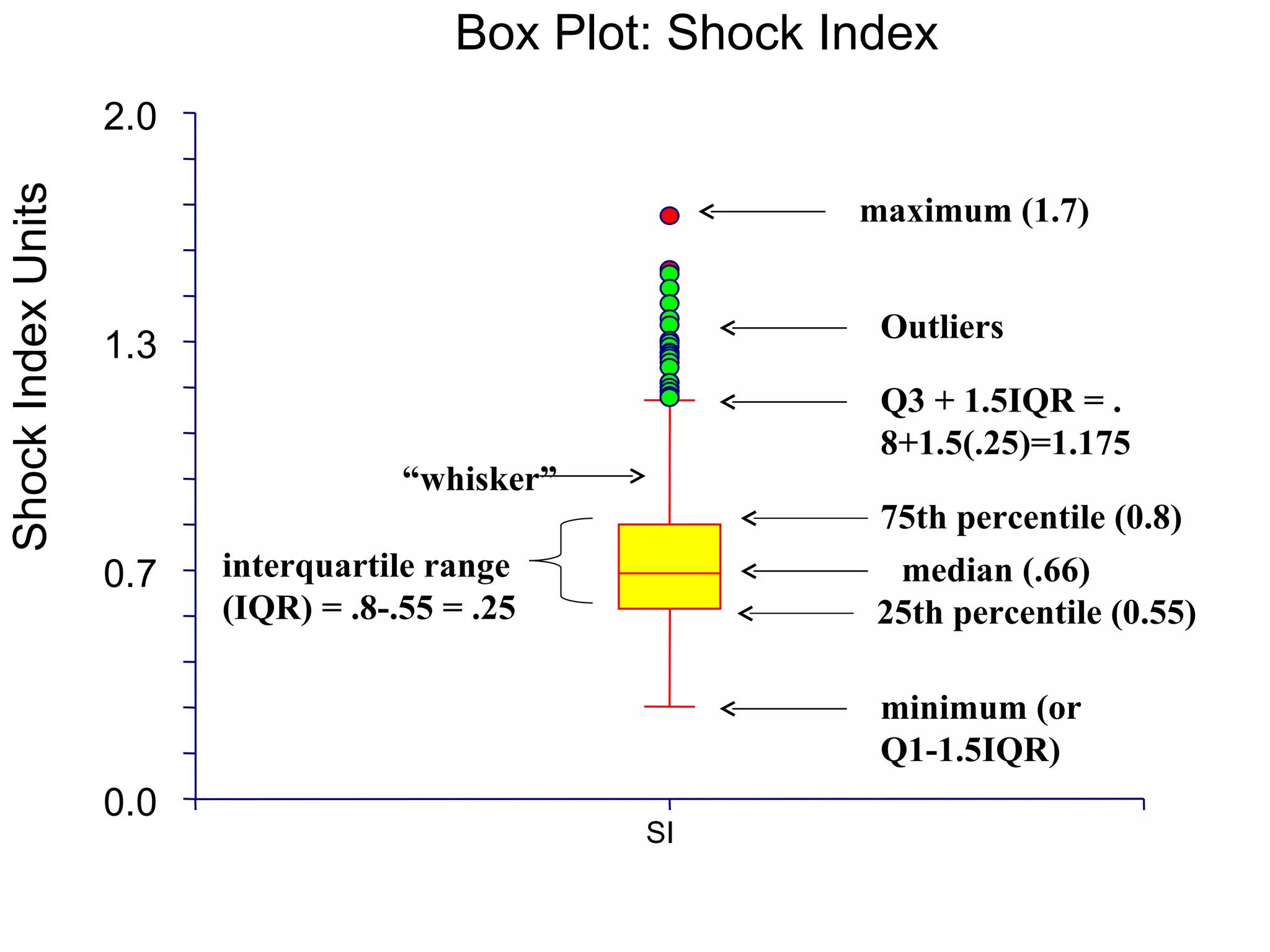
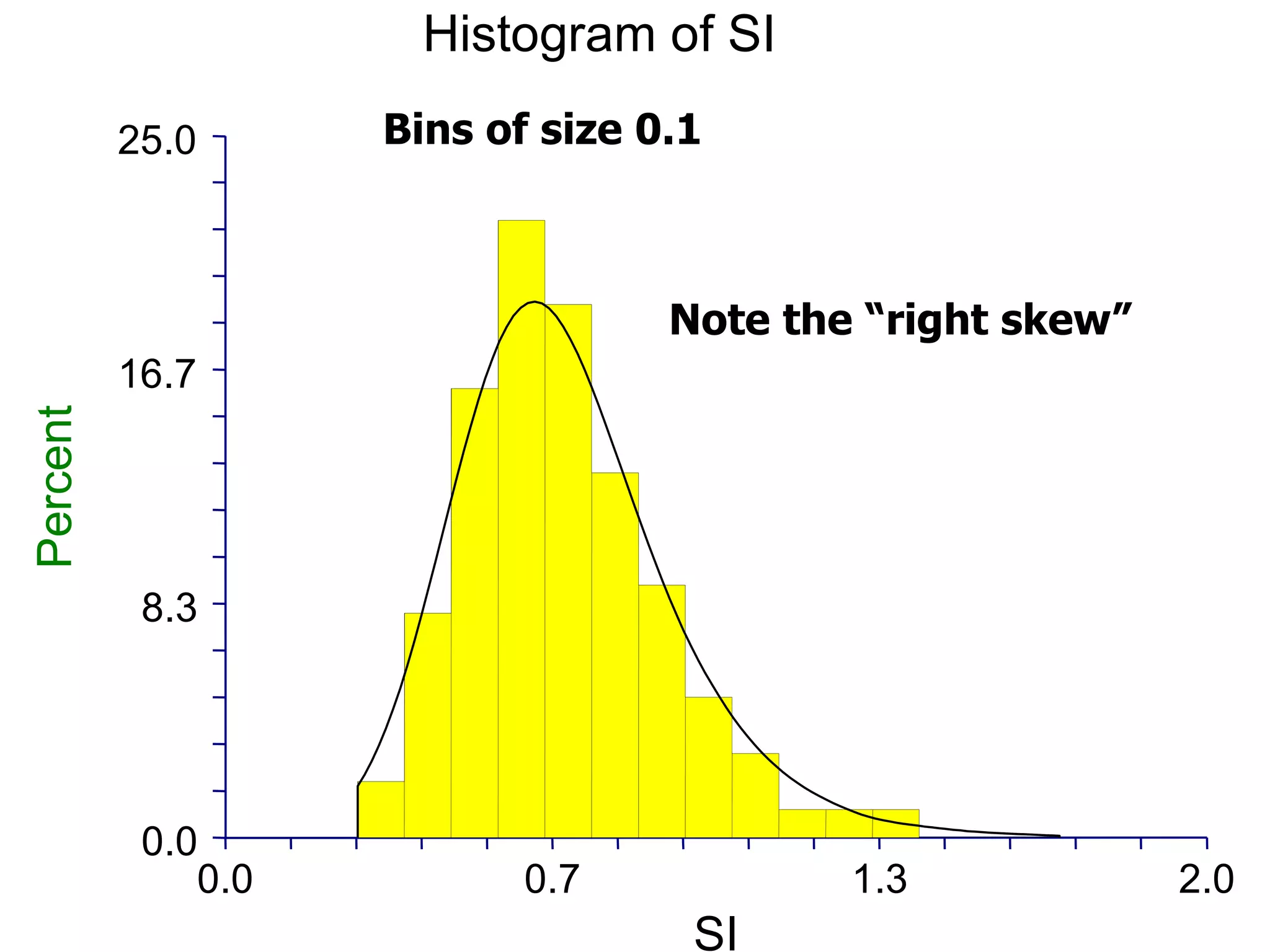
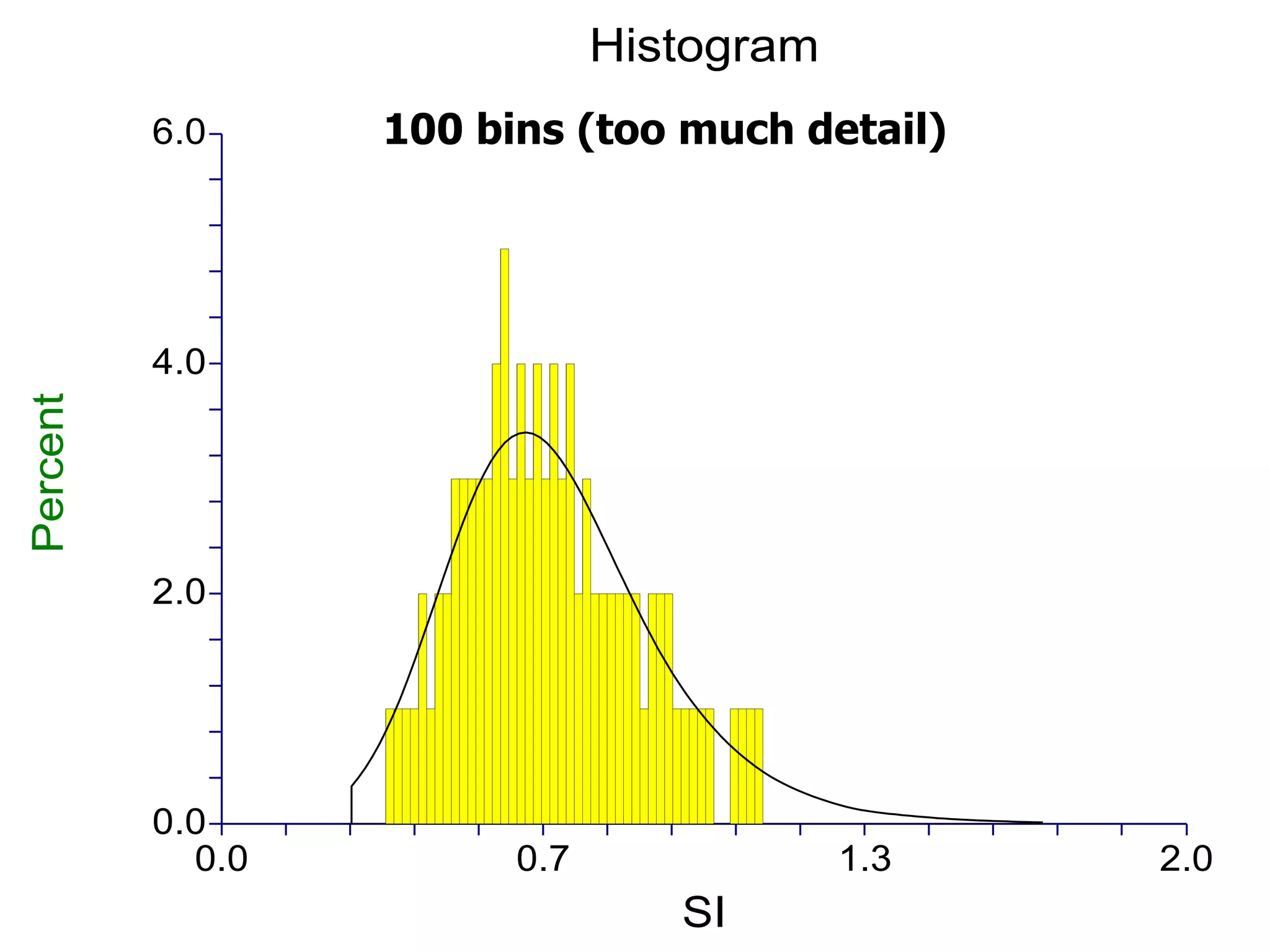
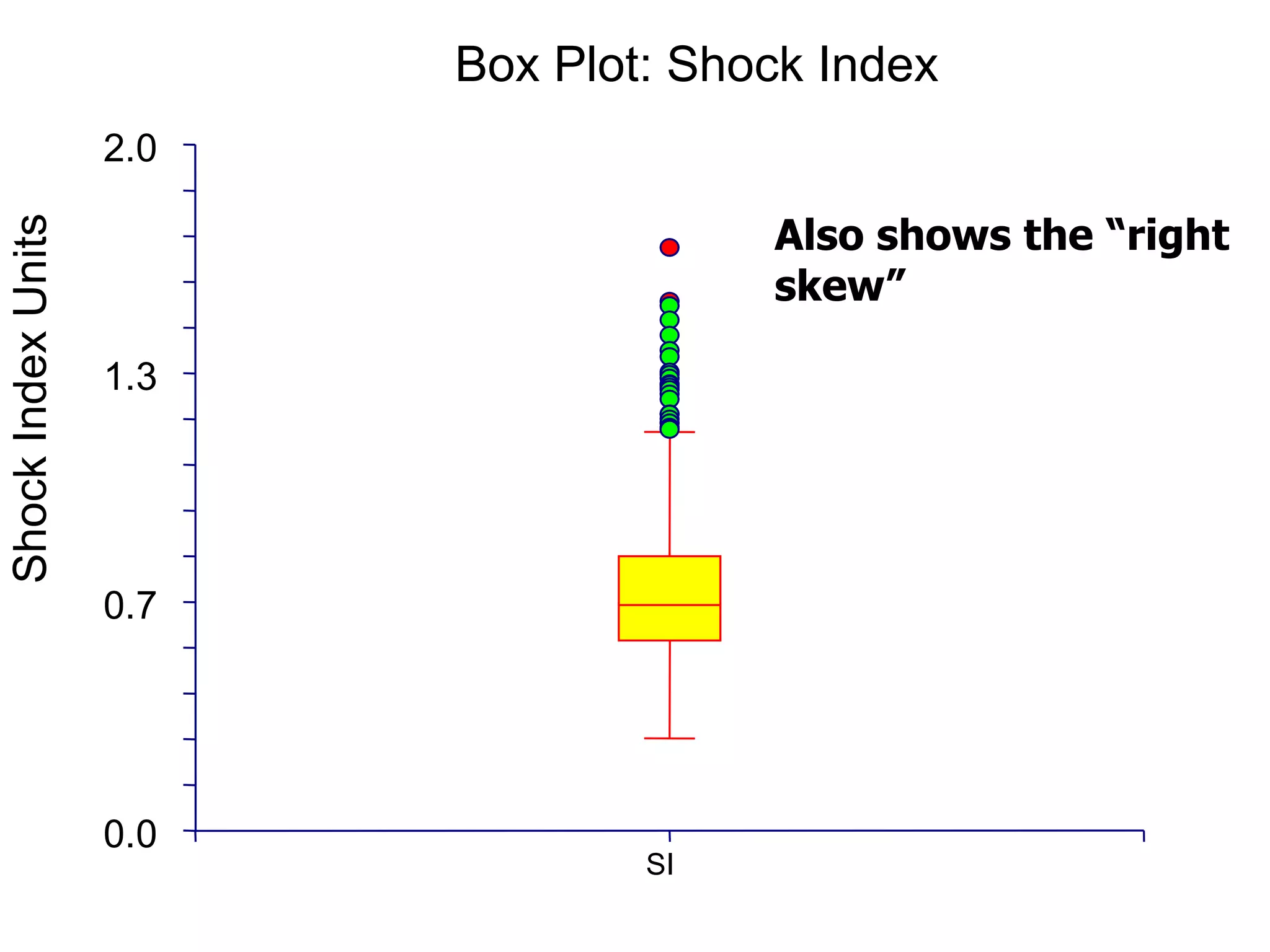
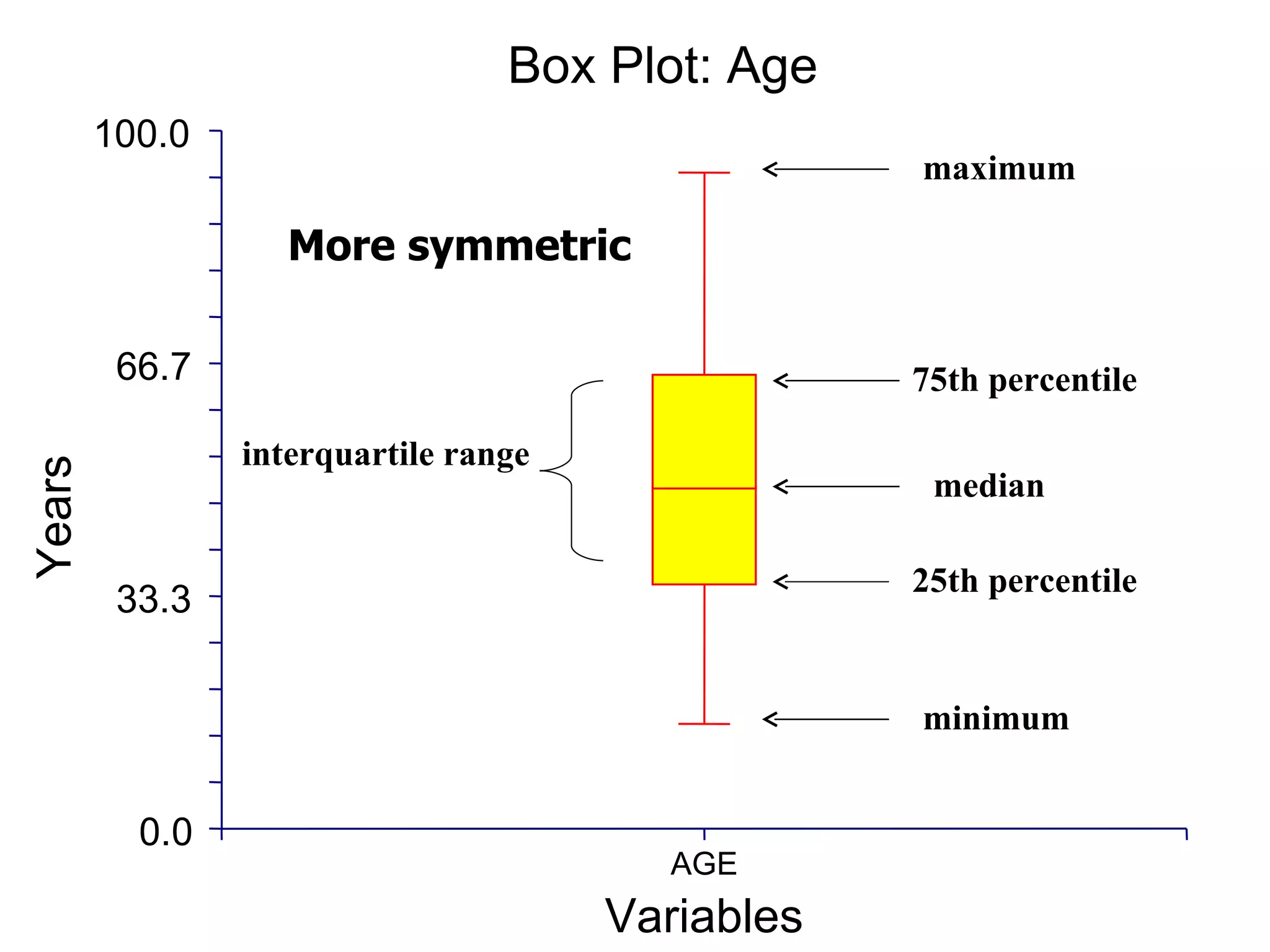
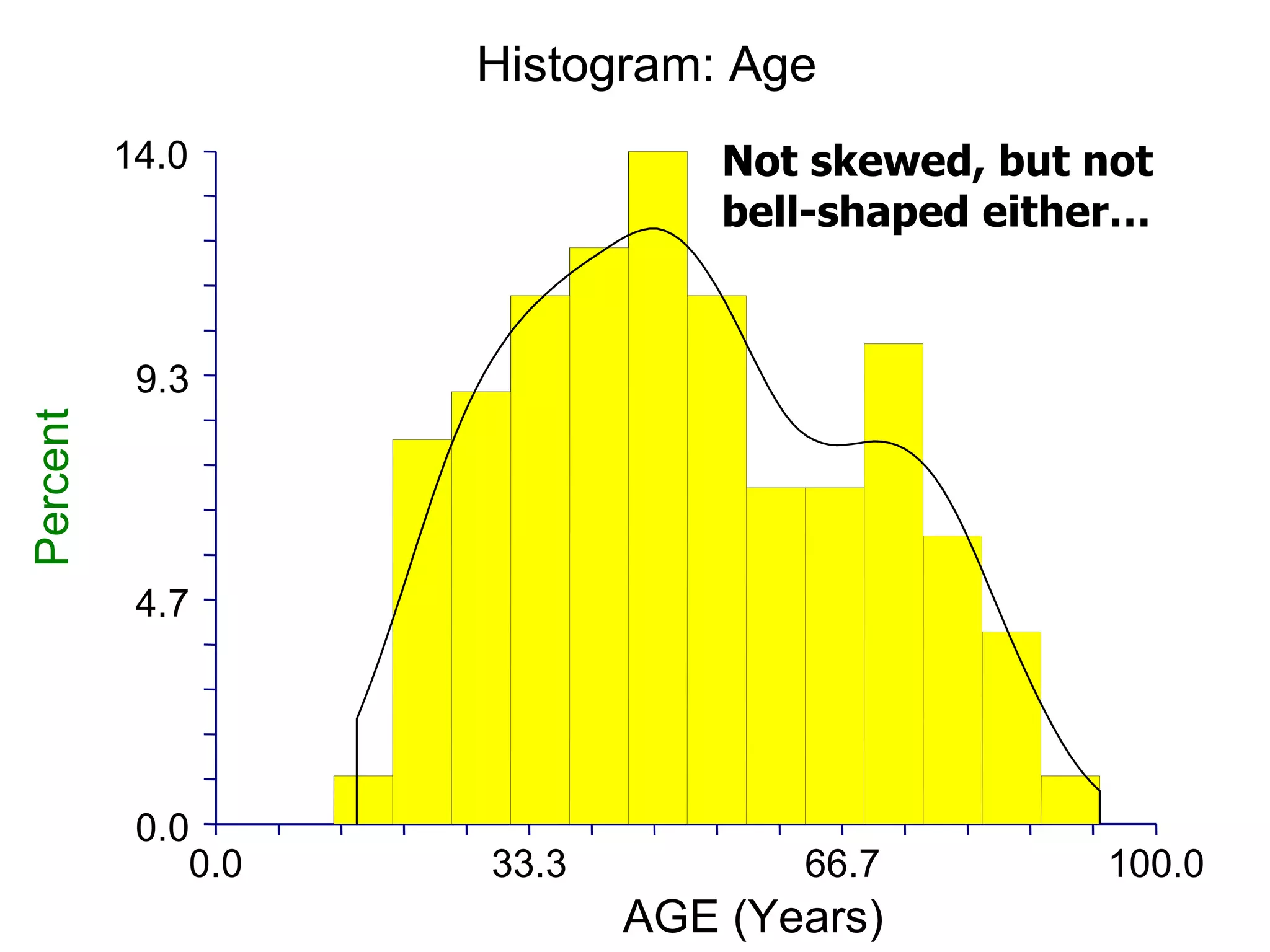
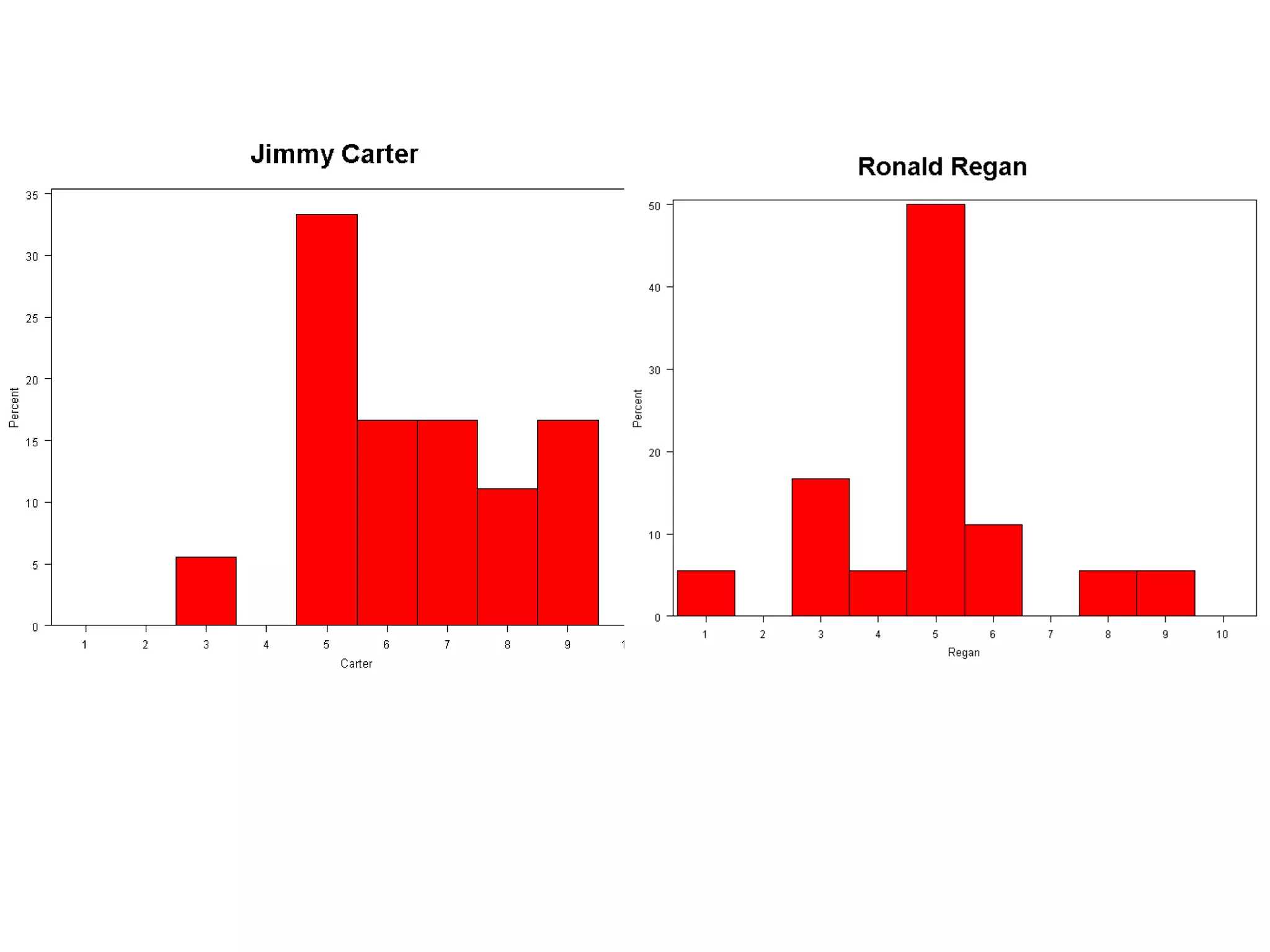
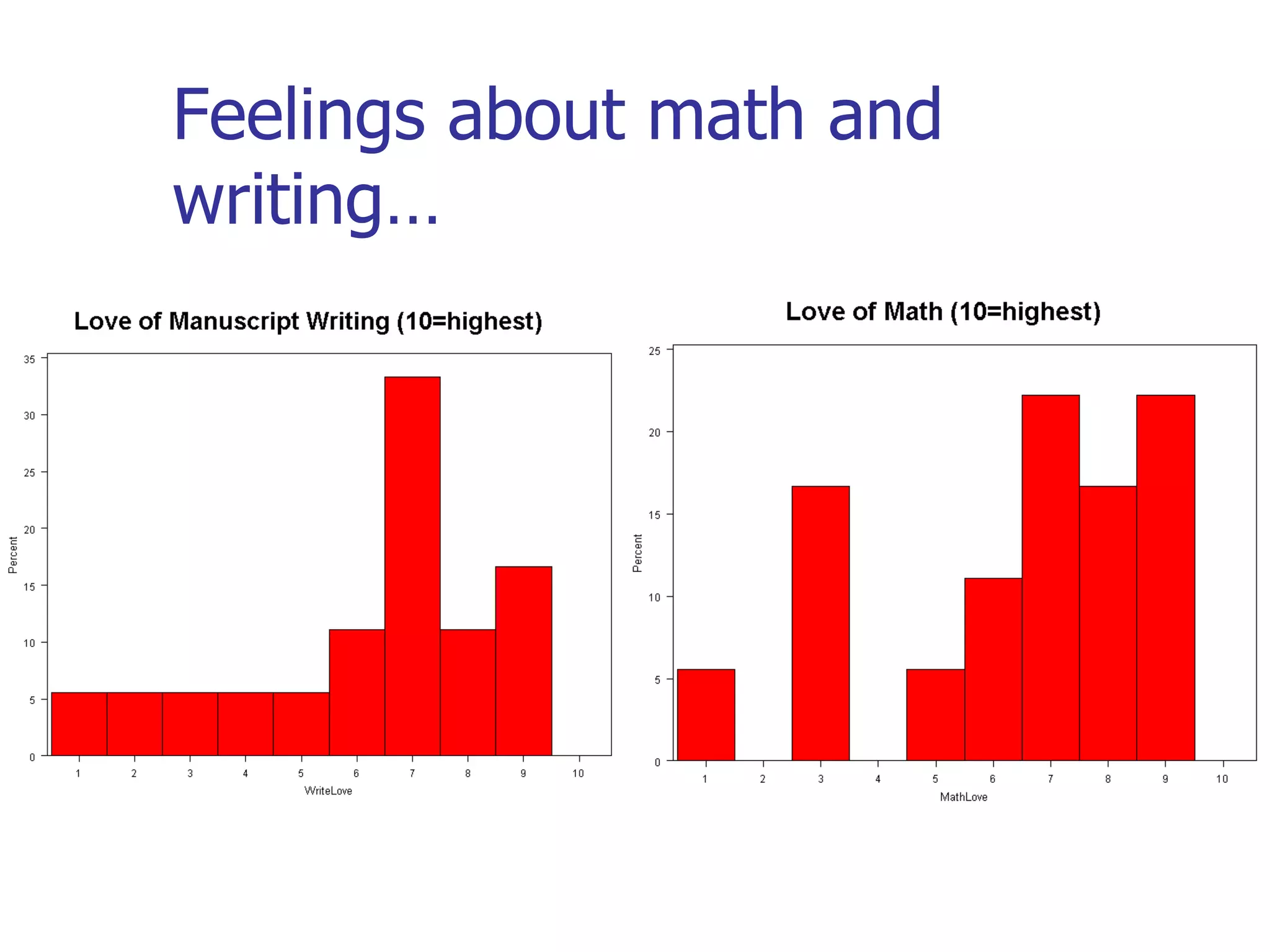
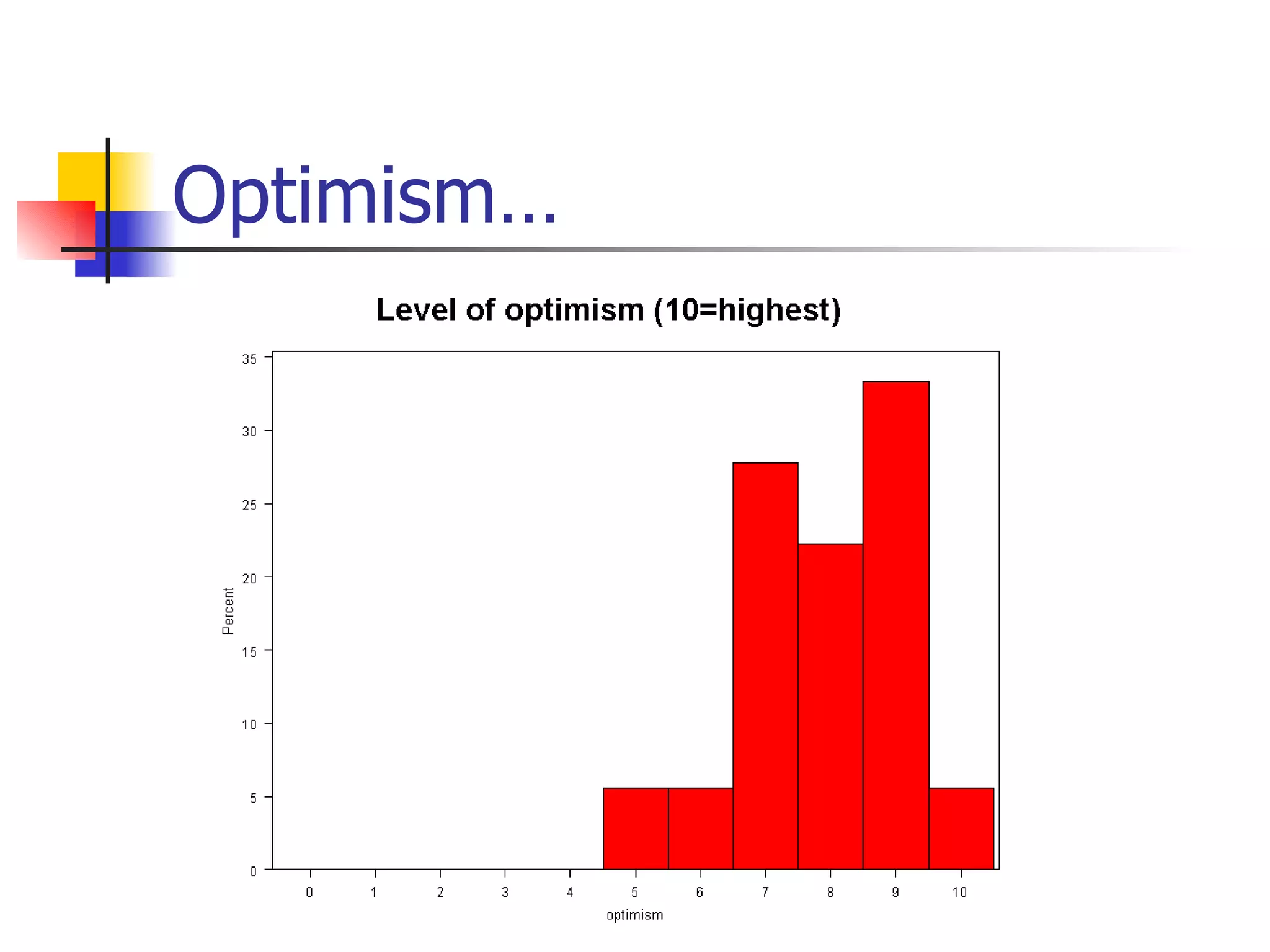
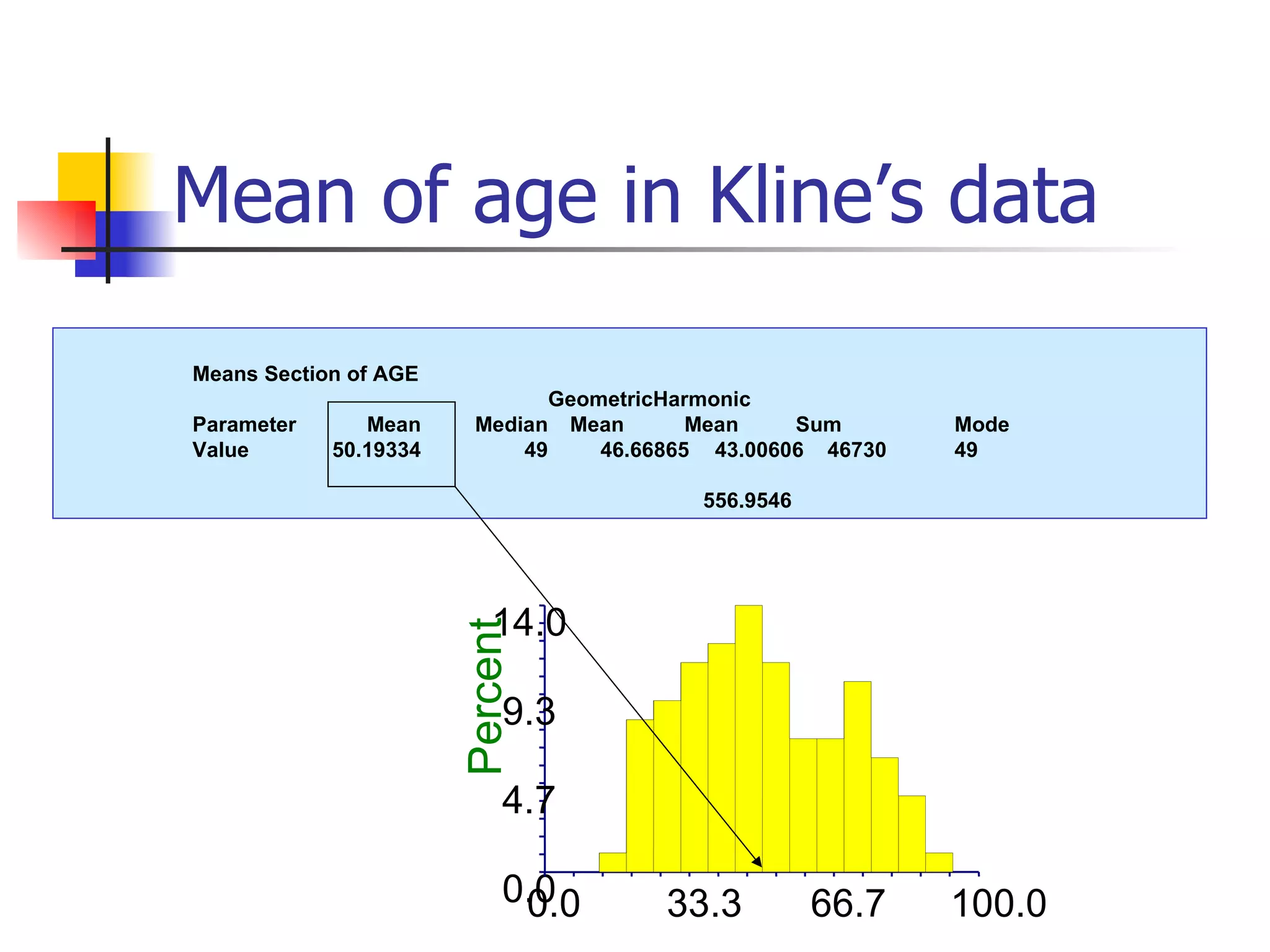
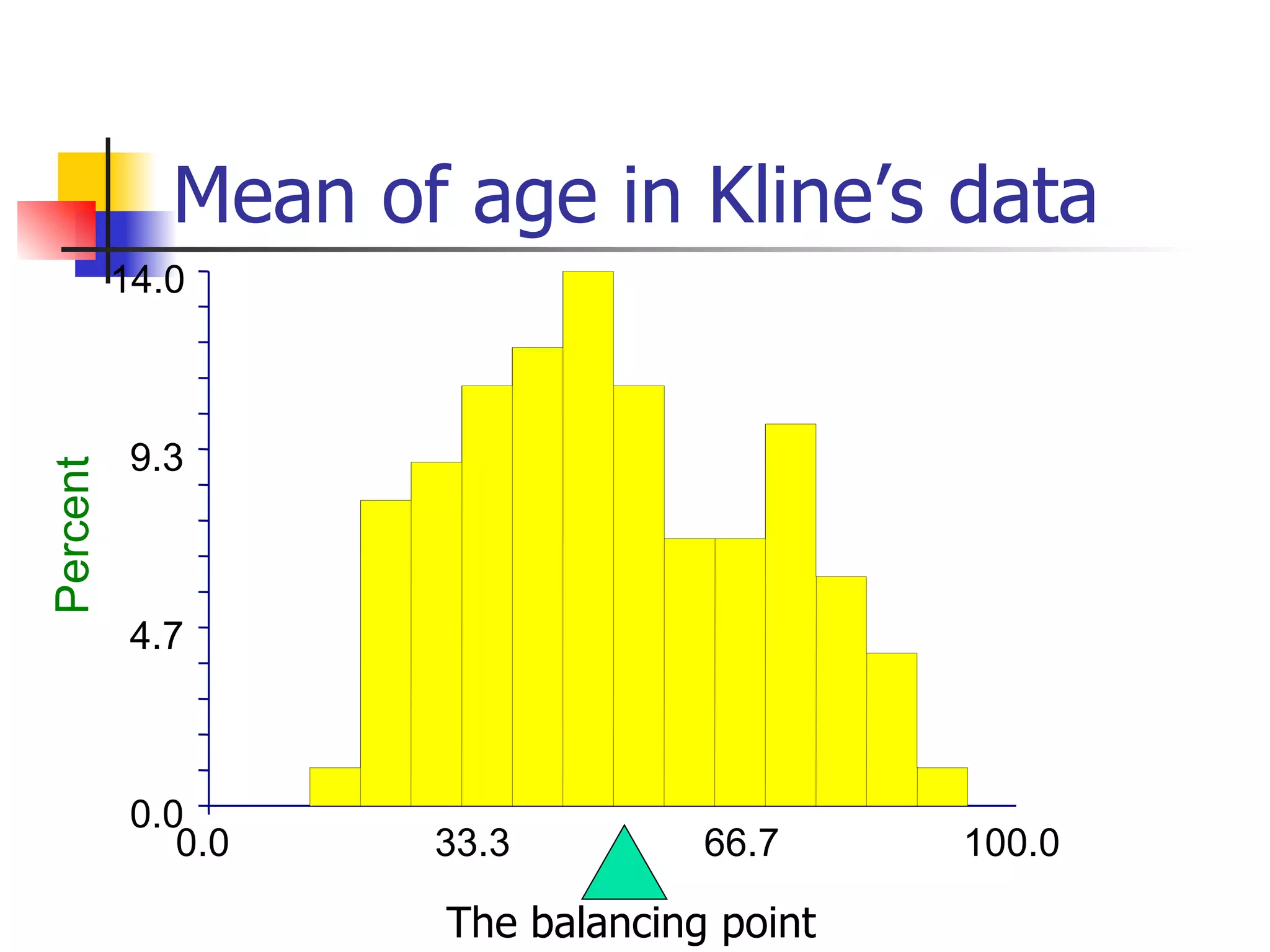
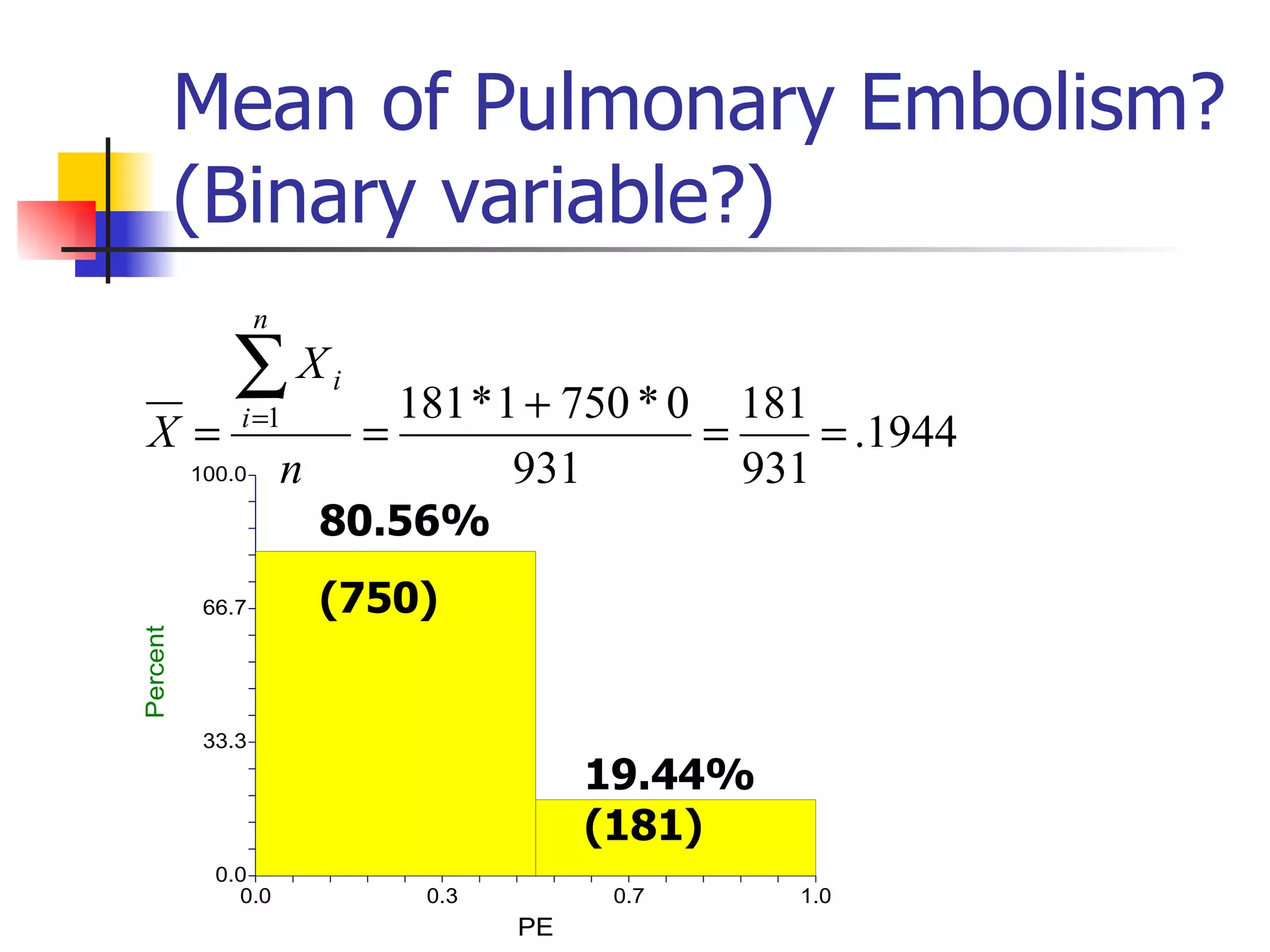
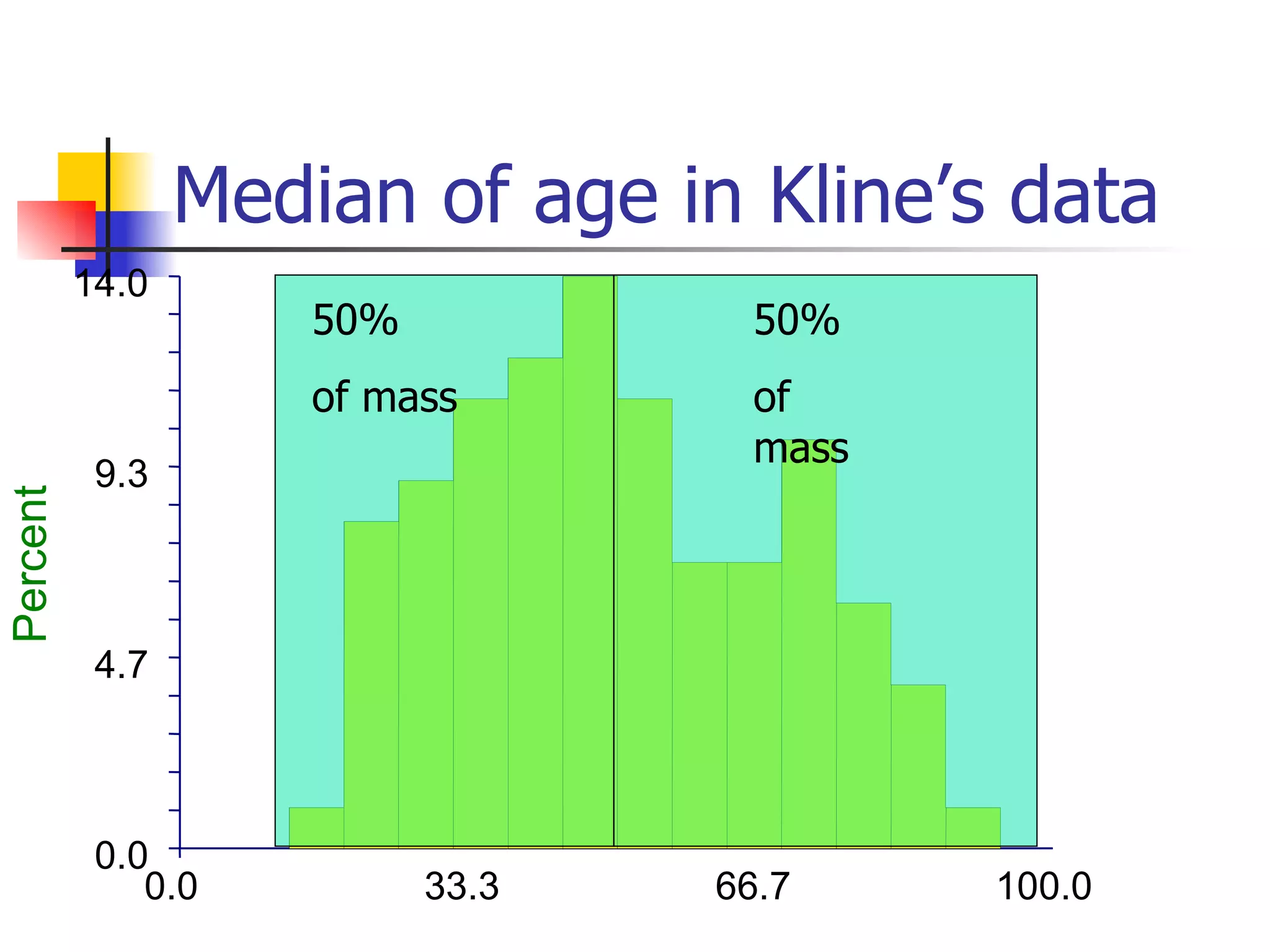
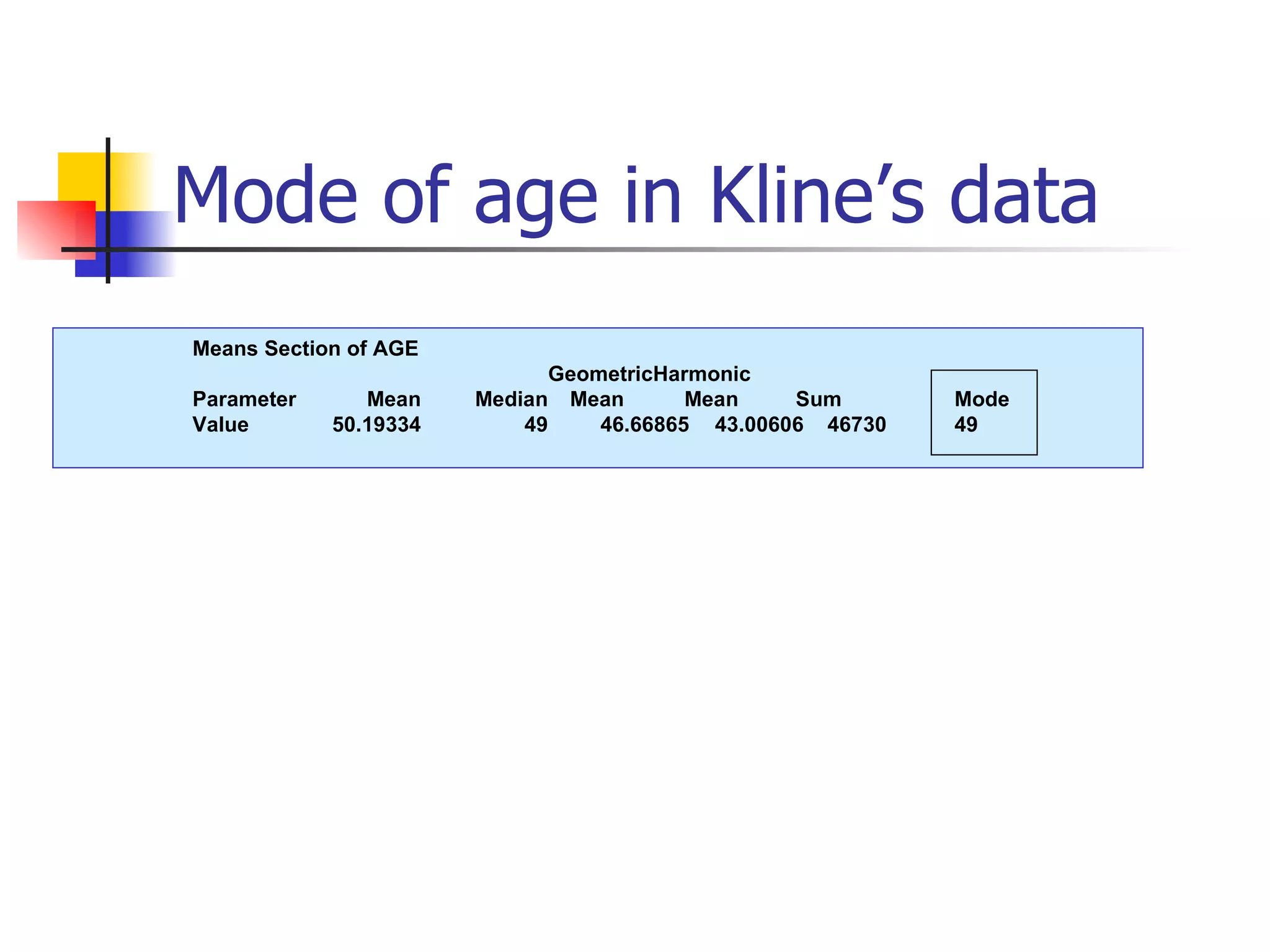
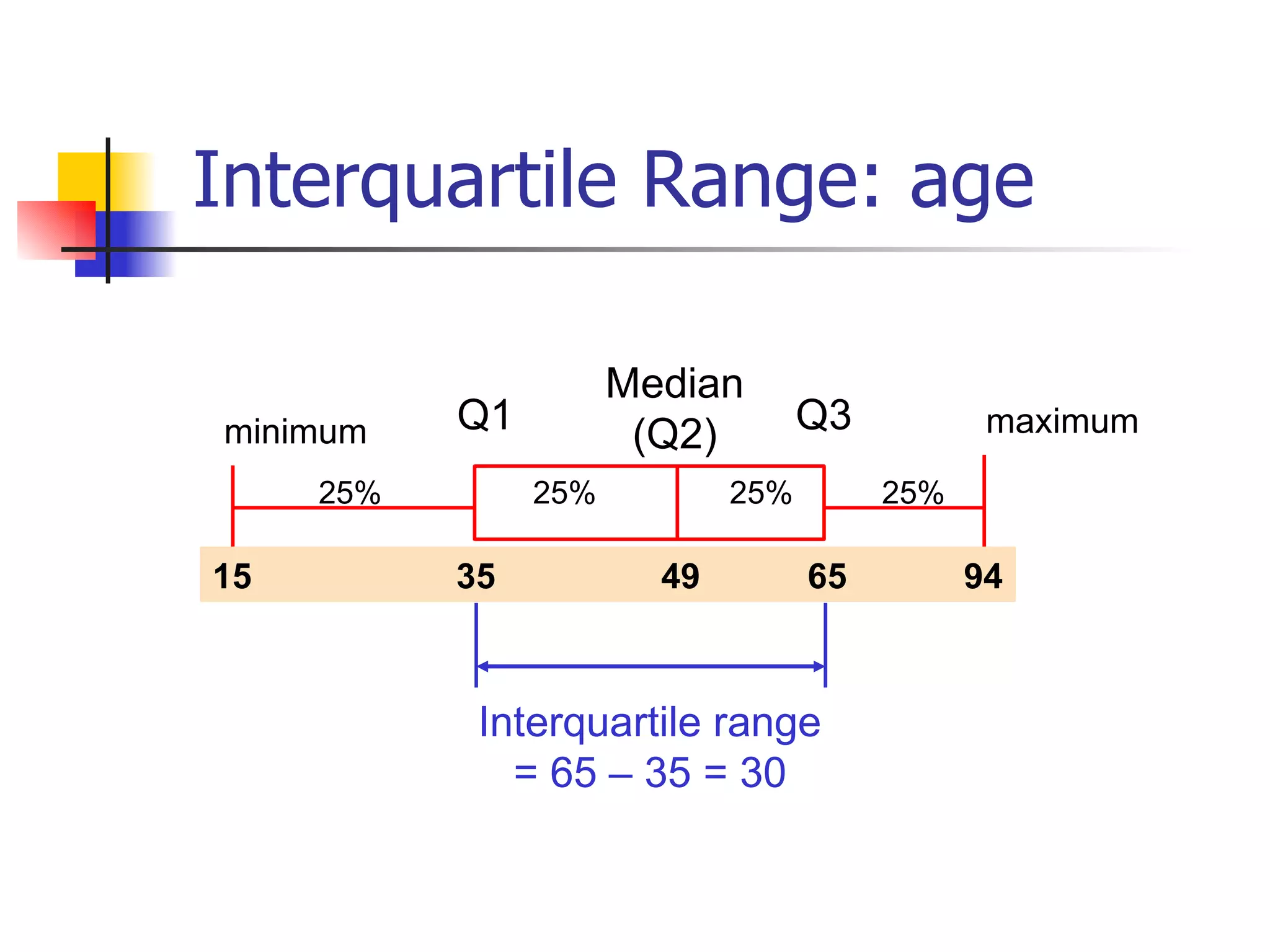
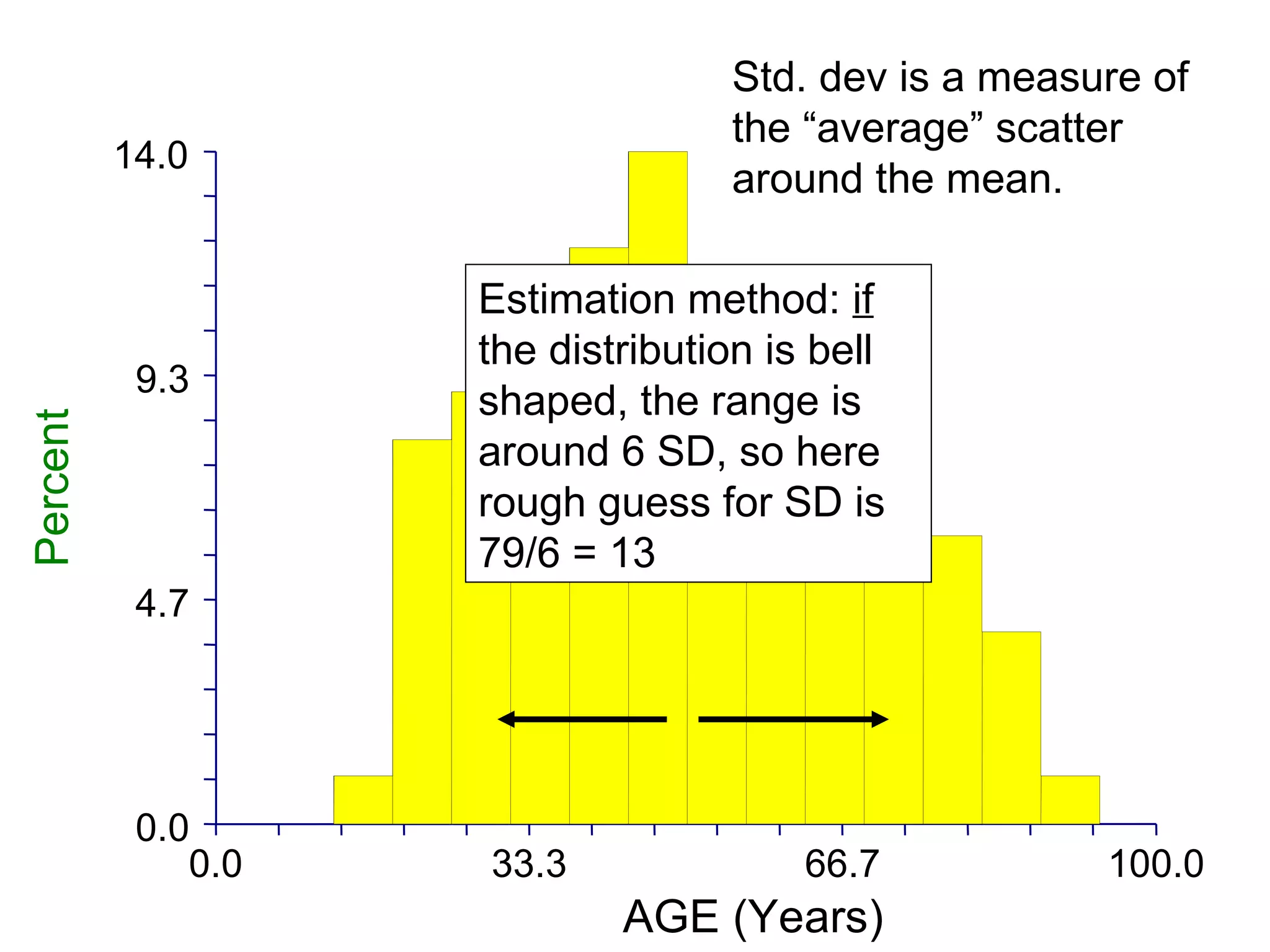
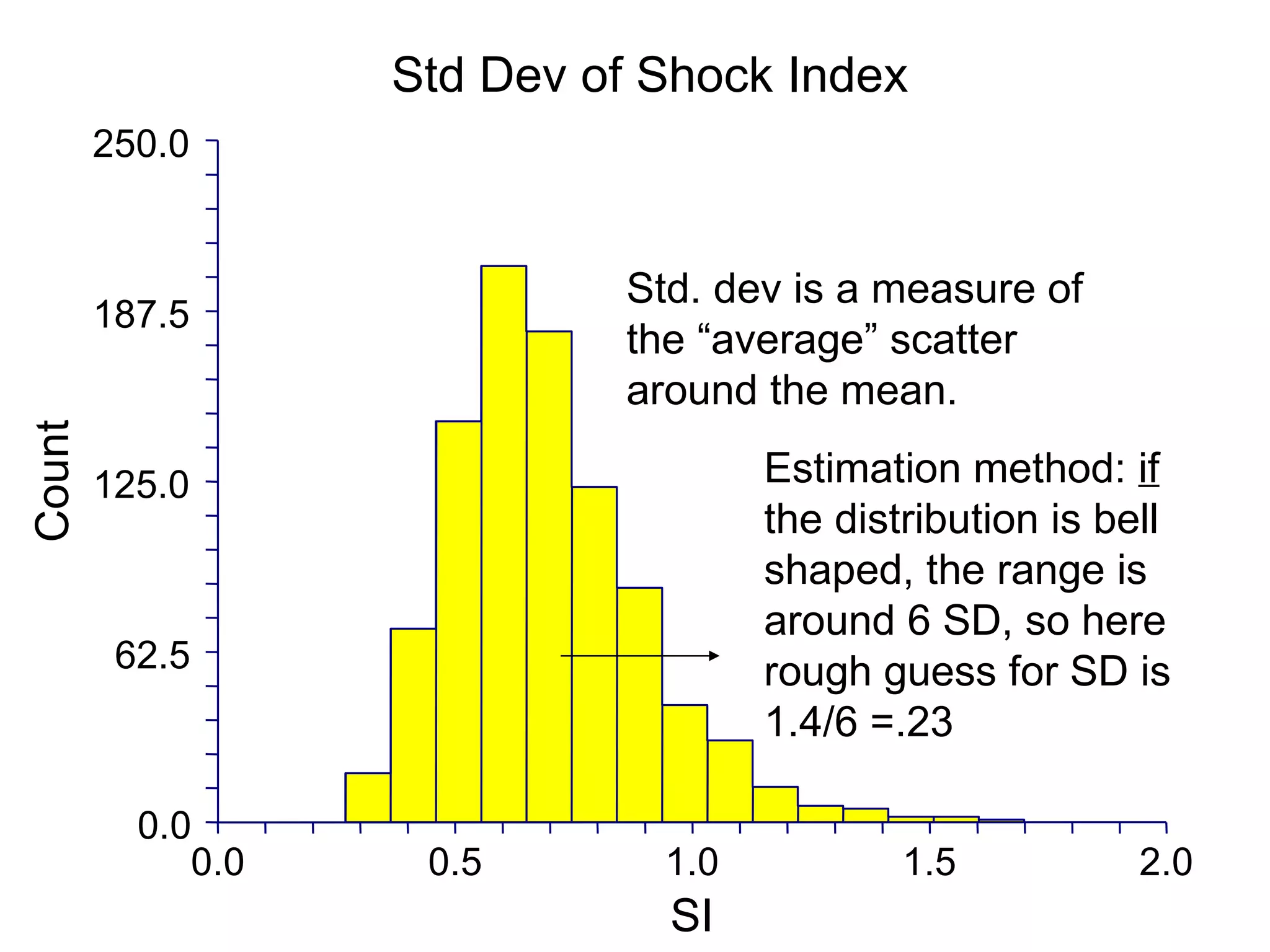
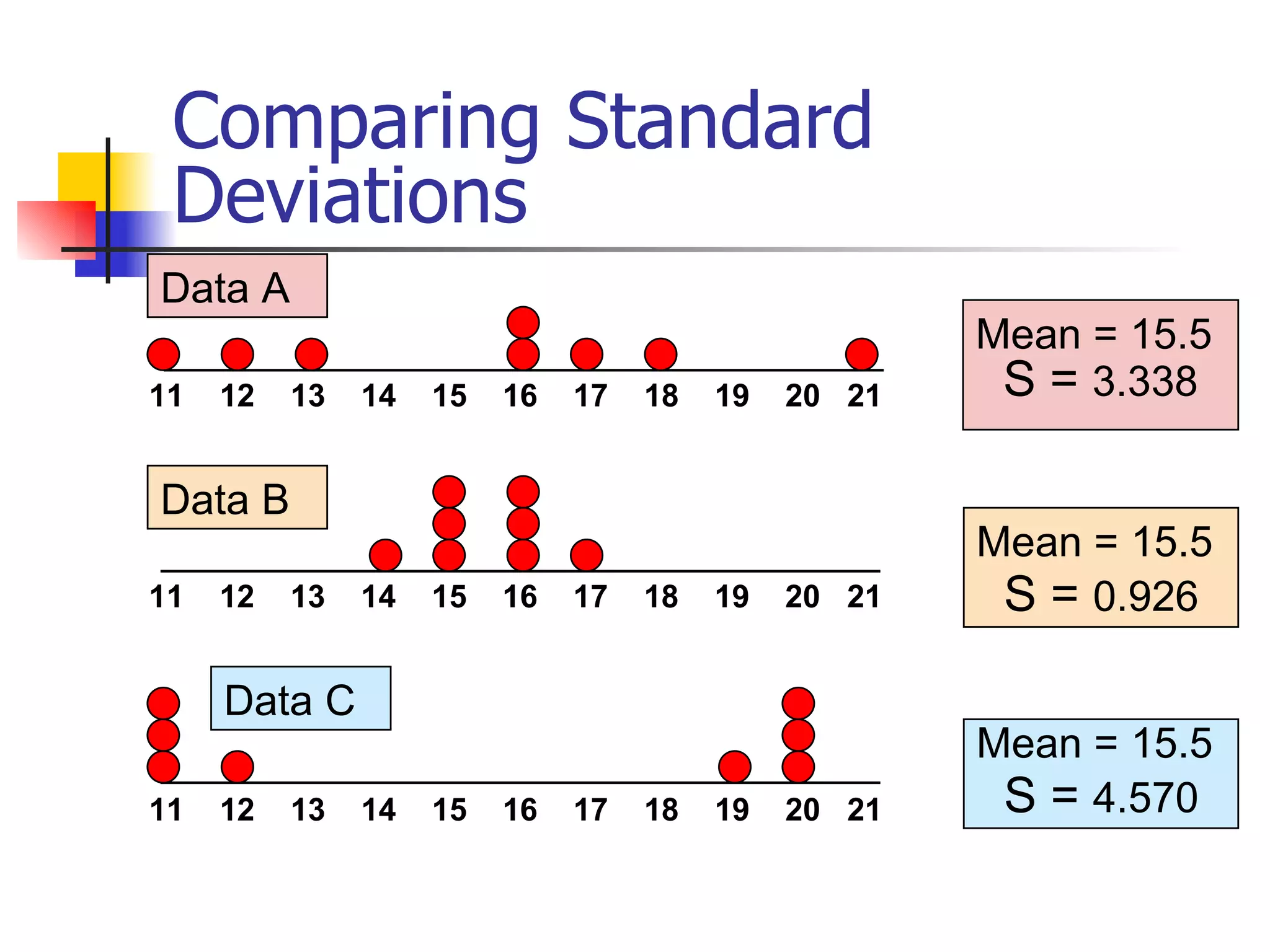
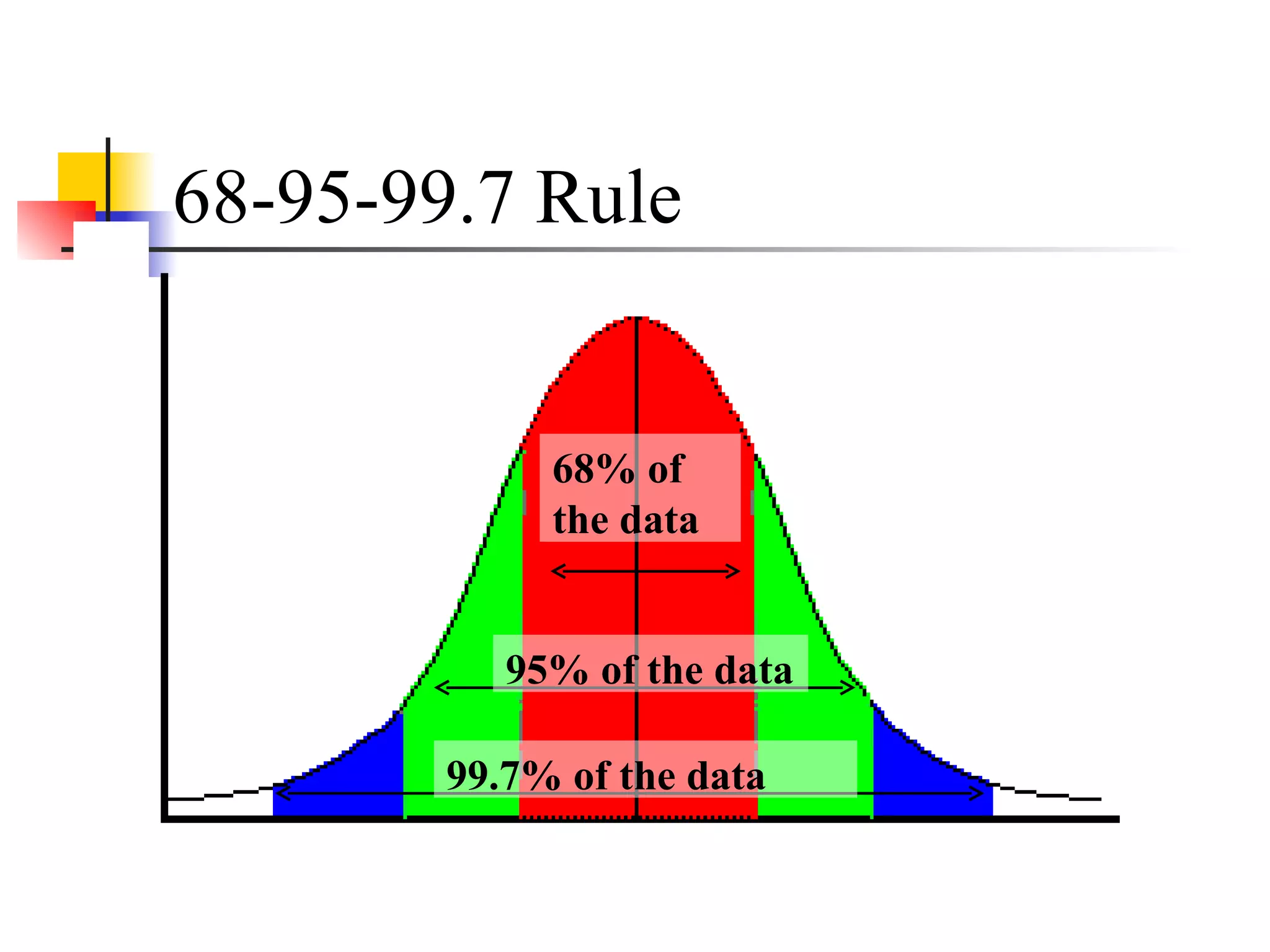
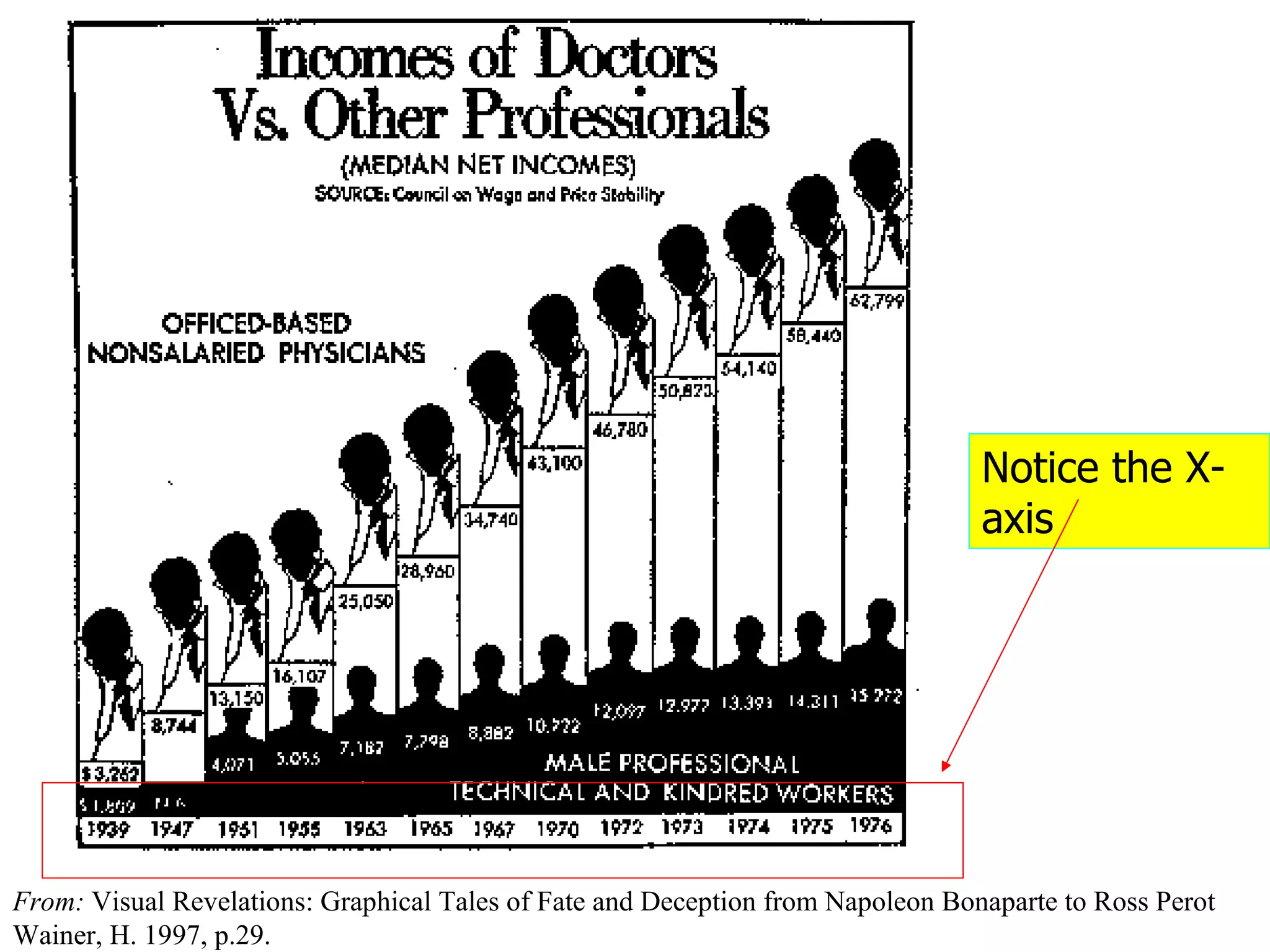
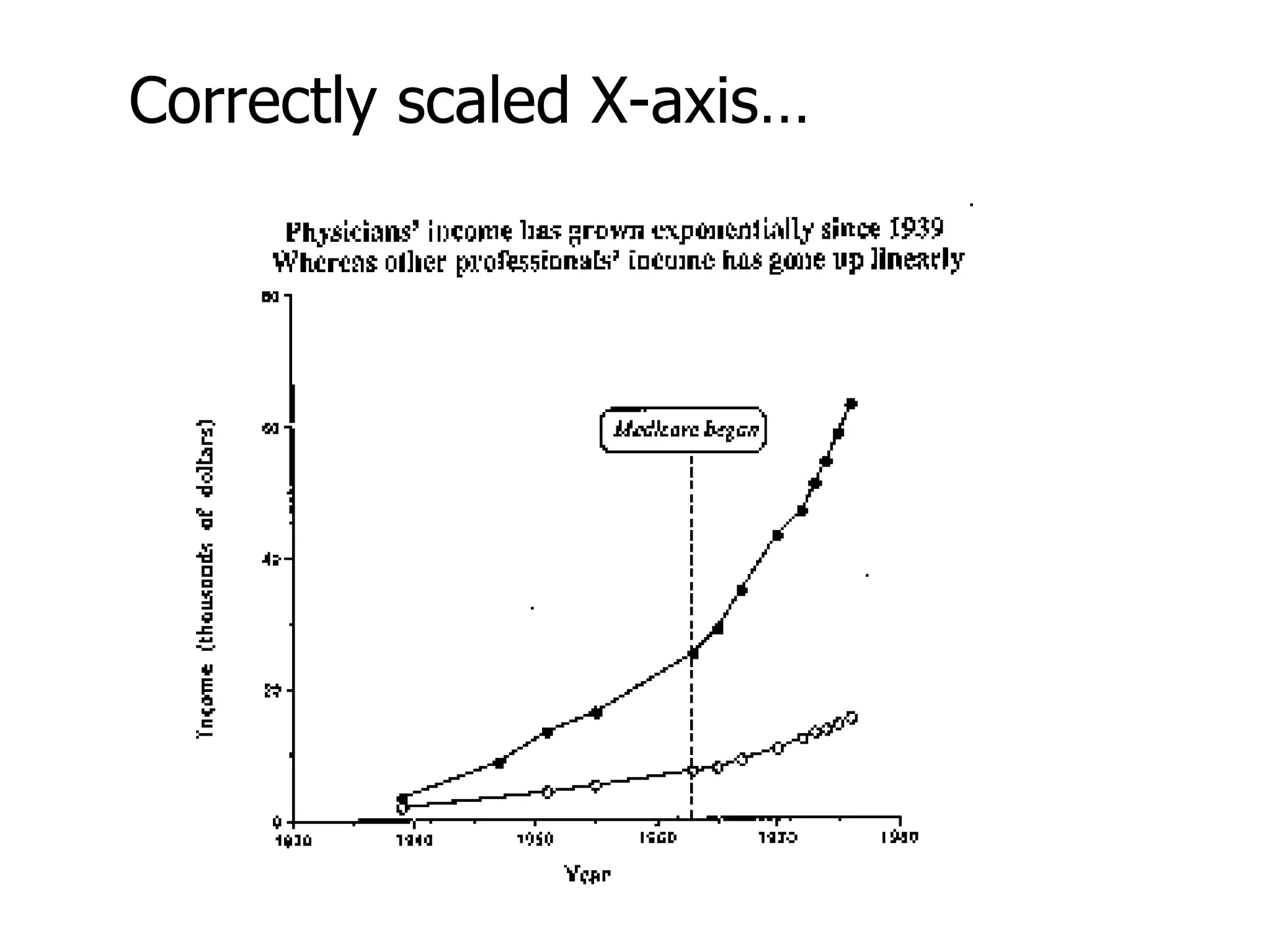
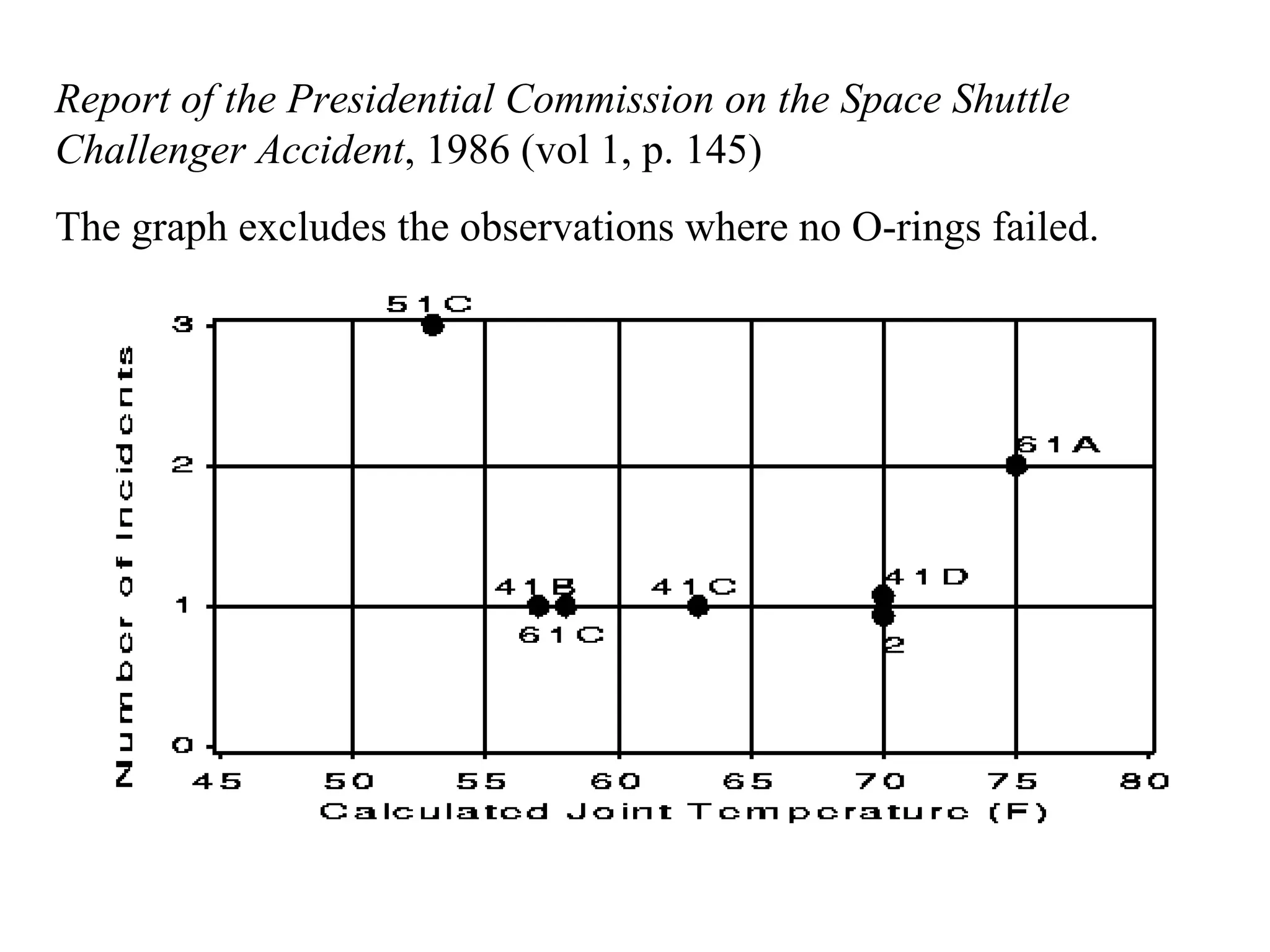
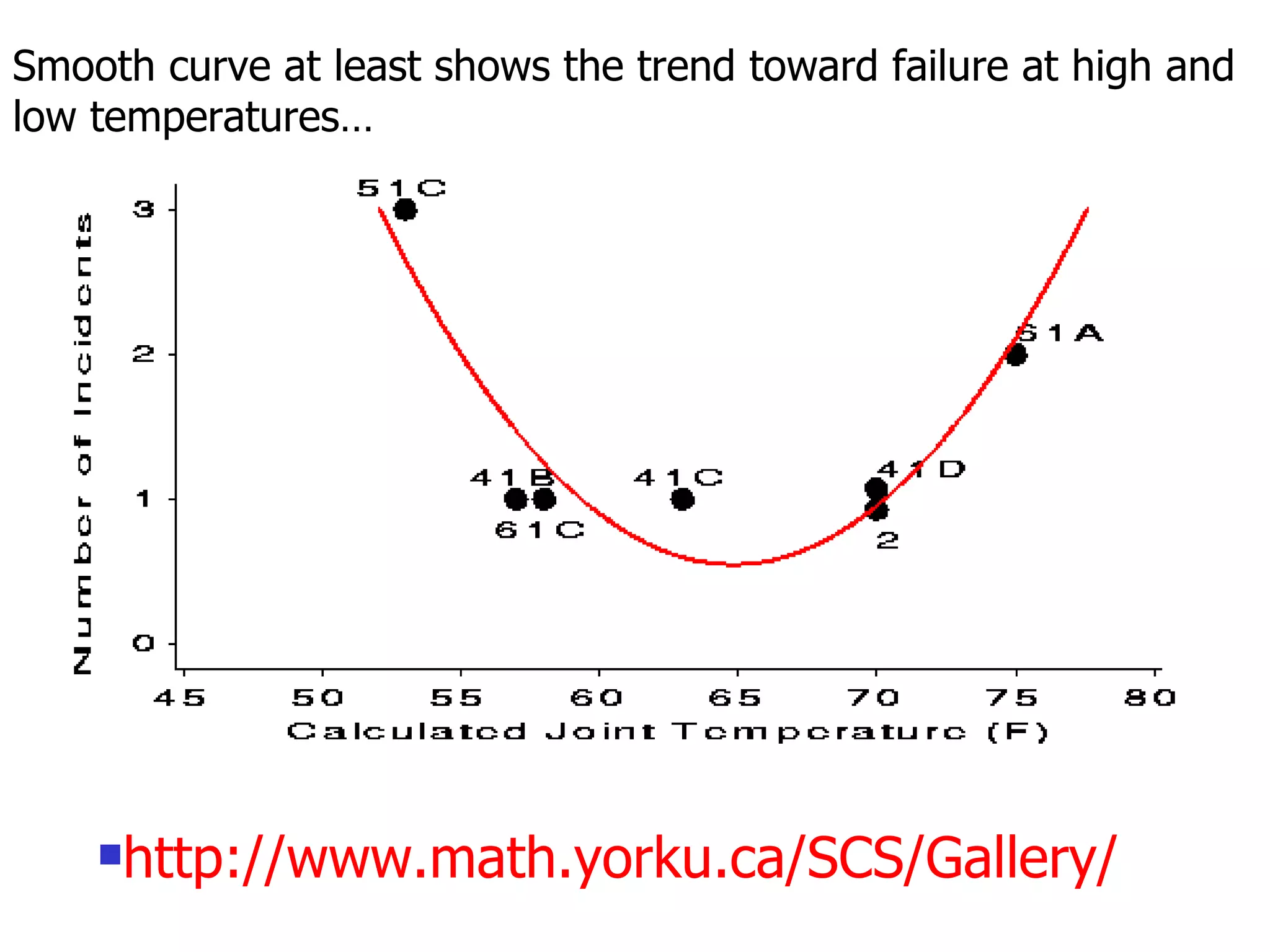
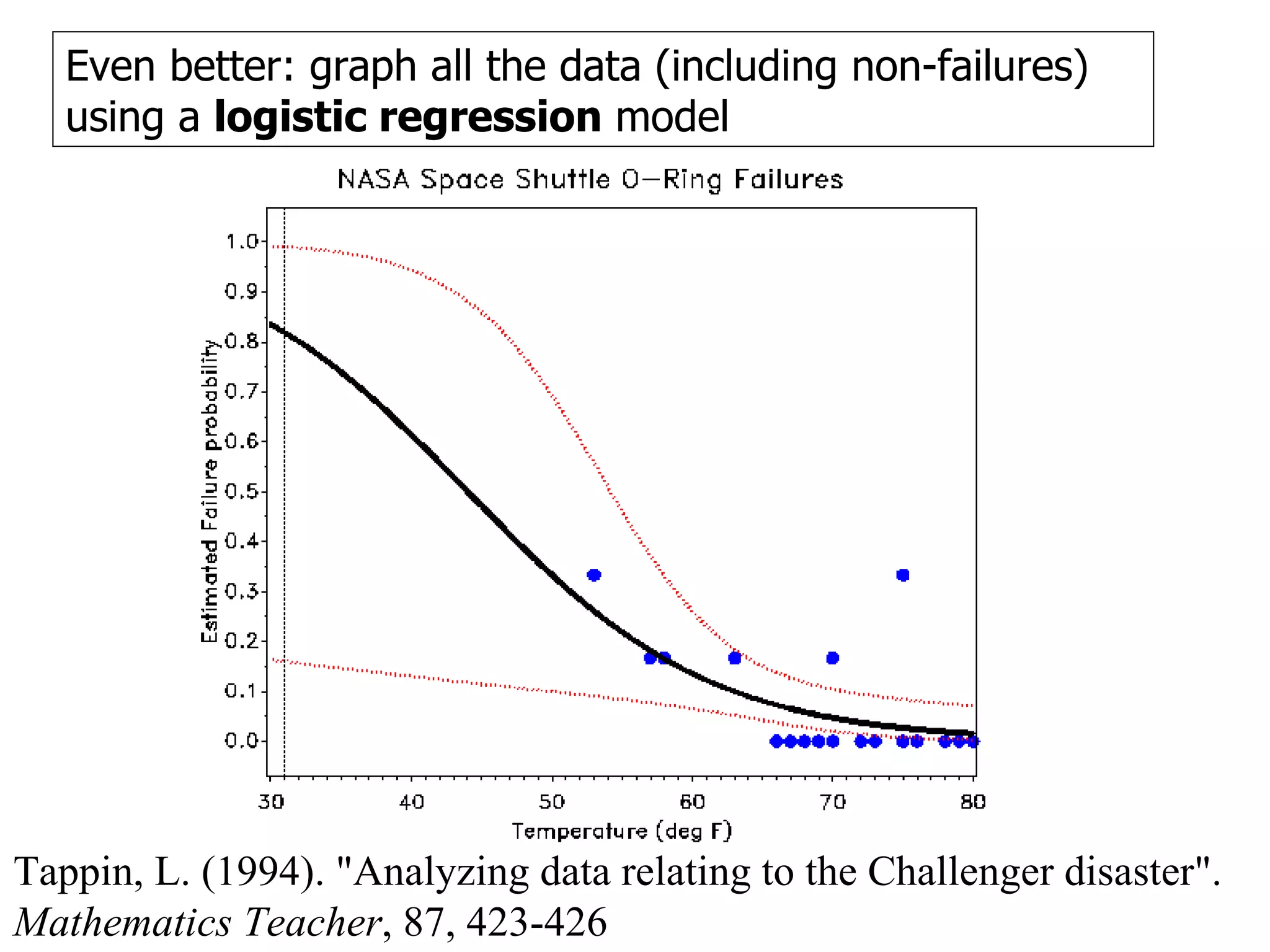
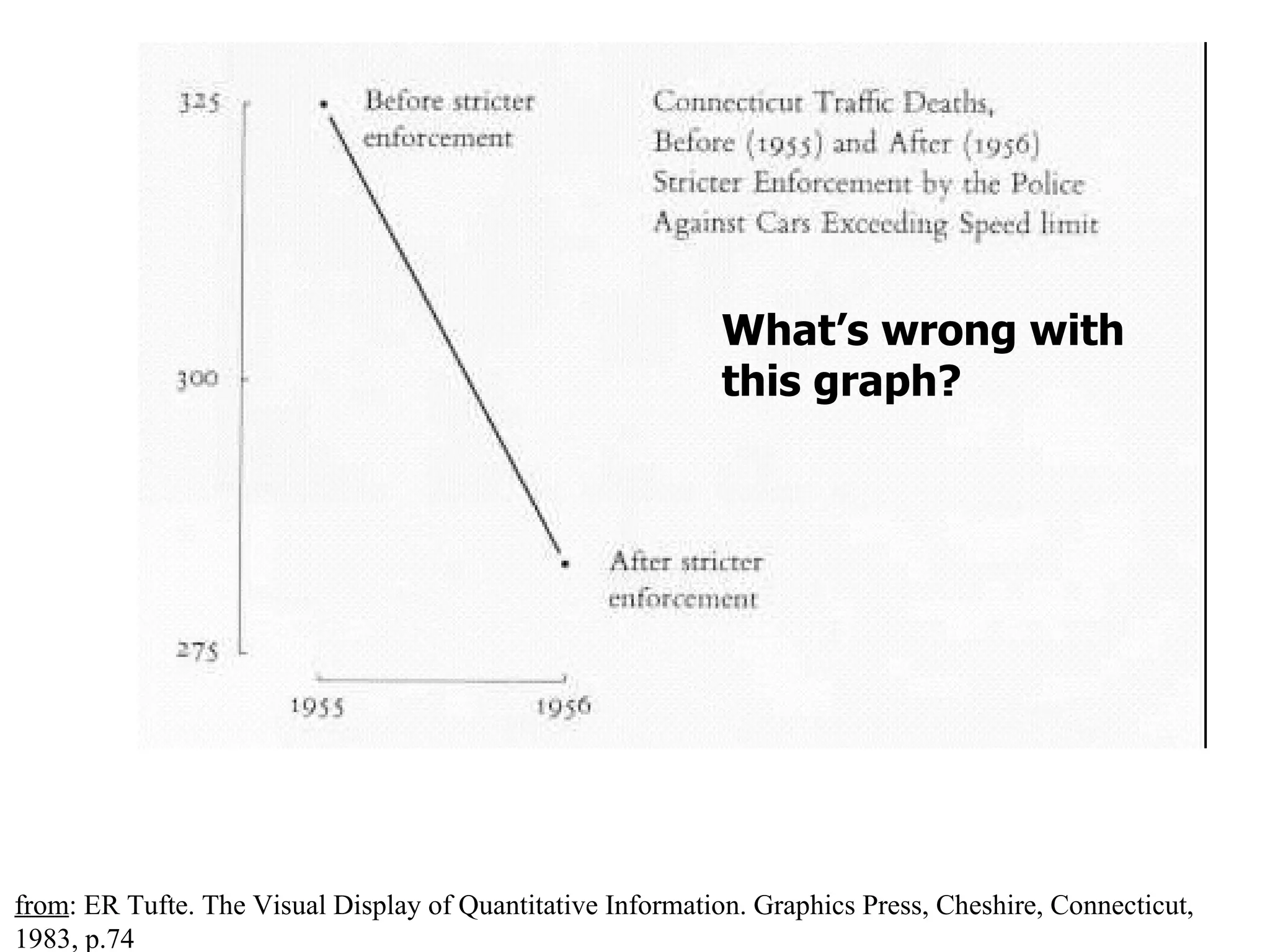
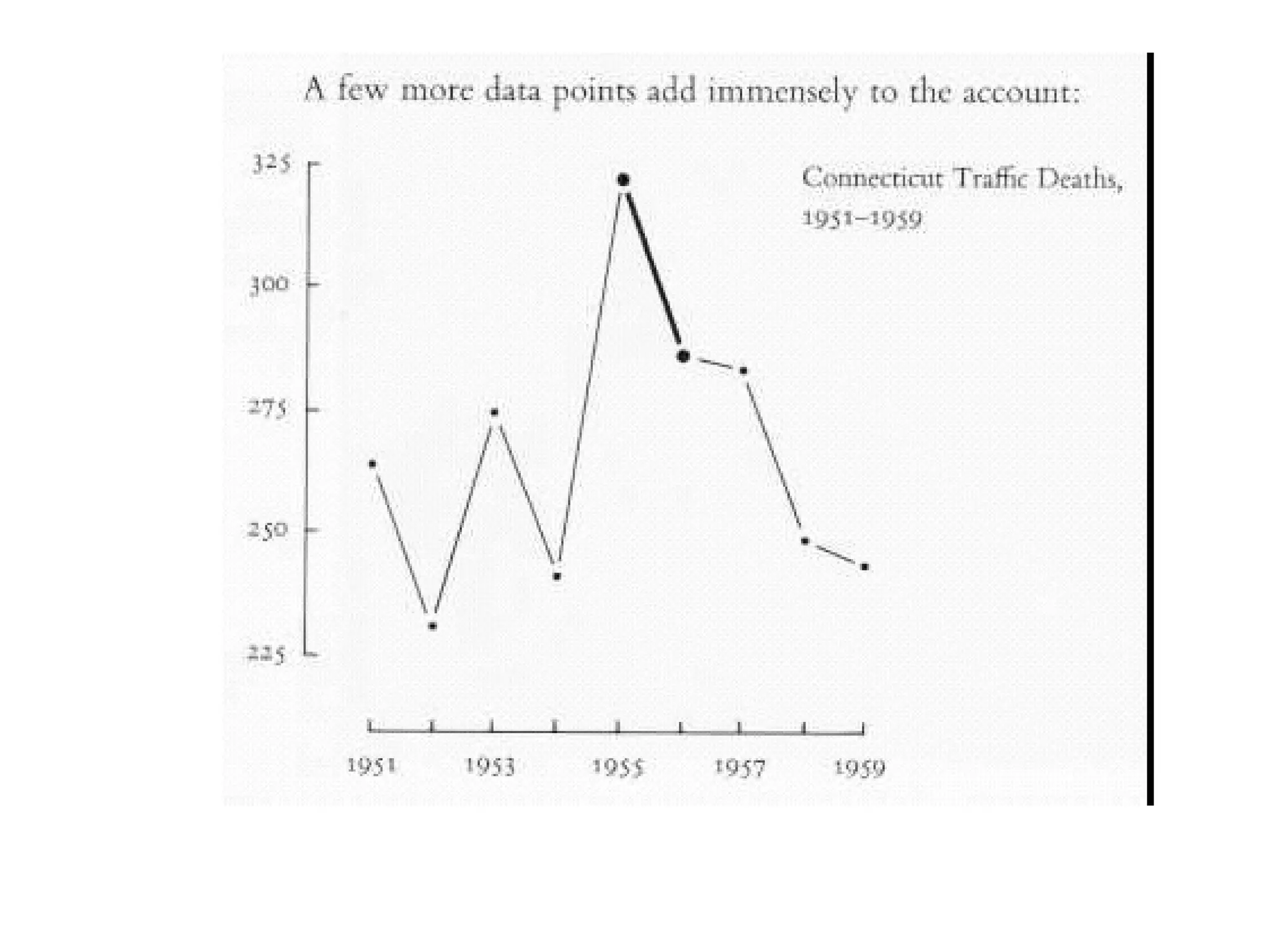
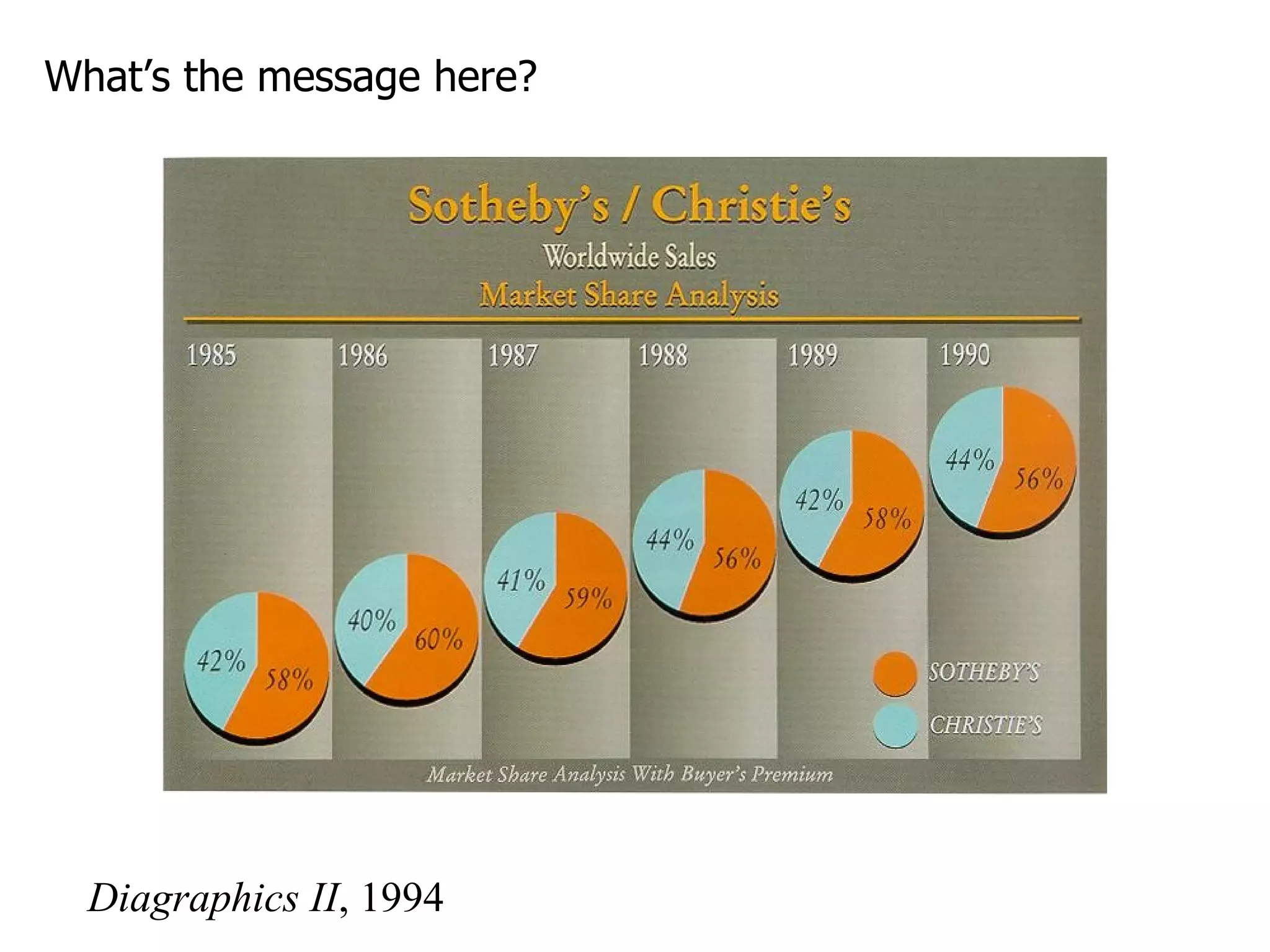
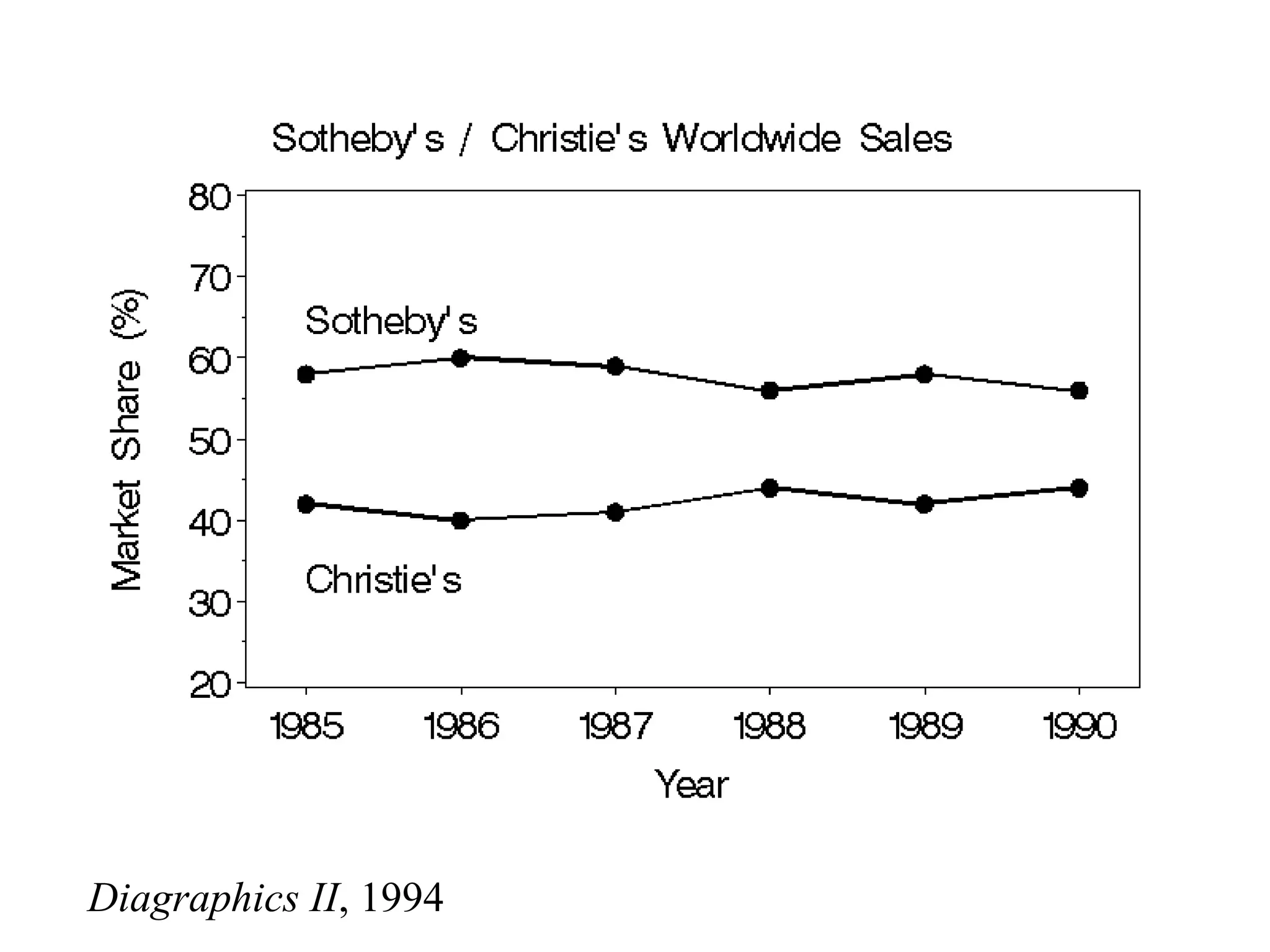
This document provides an overview of different types of variables and methods for summarizing clinical data, including descriptive statistics. It discusses categorical variables like gender and ordinal variables like disease staging. For continuous variables it explains measures of central tendency like mean, median and mode, and measures of variation like range, standard deviation, and interquartile range. Graphs for summarizing univariate data are also covered, such as bar charts for categorical variables and histograms and box plots for continuous variables.