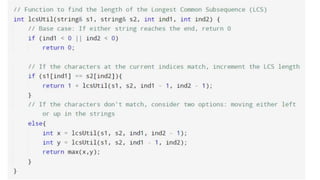
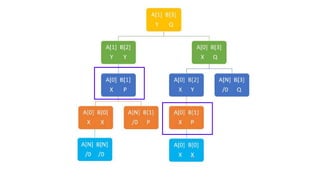
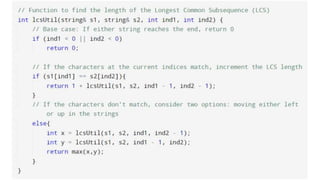
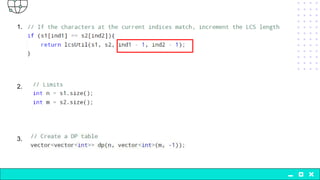
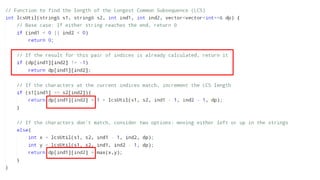
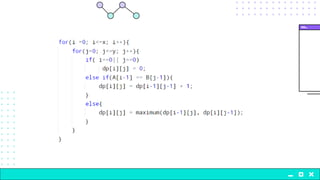
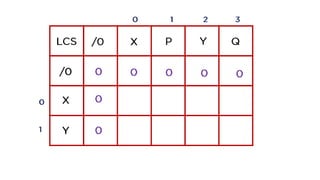
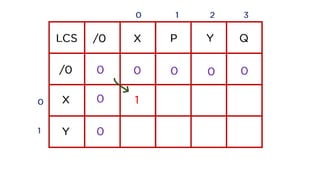
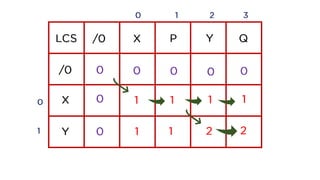
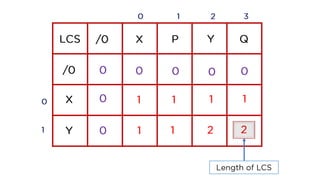
The document discusses the problem of finding the longest common subsequence (LCS) between two strings, explaining definitions and providing examples. It outlines different approaches to solve the problem, including brute force, recursion, memoization, and tabulation, detailing their respective complexities. The document also includes references and credits for resources used in the presentation.

1. Longest common
subsequence
(LCS)

2. Table of contents
01
03
02
04
Understanding
the problem Recursion
Memoization Tabulation

3. Understanding
The Problem
01

4. Definations
A subsequence of a string is a new string generated from the original
string with some characters (can be none) deleted without changing
the relative order of the remaining characters.
e.g. A = bacad (Total possible substring: 2m )
Substrings: ad, ac, bac, acad, bacad, bcd.
A common subsequence of two strings is a subsequence that is
common to both strings.
A = bacad
B = accbadcb
common subsequence : ad, ac, bac, acad.
The longest common subsequence (LCS) of A and B: acad.

5. Problem Statement
Given two strings s1 and s2, return the length of their longest
common subsequence. If there is no common subsequence,
return 0.
Example:
Input: s1= "abcde", s2= "ace"
Output: 3
Explanation: The longest common subsequence is "ace" and its
length is 3.

6. Let’s try another example
INPUT: two strings
OUTPUT: longest common subsequence
ACTGAACTCTGTGCACT
TGACTCAGCACAAAAAC

7. Let’s try another example
INPUT: two strings
OUTPUT: longest common subsequence
ACTGAACTCTGTGCACT
TGACTCAGCACAAAAAC

8. Let’s try another example
INPUT: two strings
OUTPUT: longest common subsequence
ACTGAACTCTGTGCACT
TGACTCAGCACAAAAAC

9. Let’s try another example
INPUT: two strings
OUTPUT: longest common subsequence
ACTGAACTCTGTGCACT
TGACTCAGCACAAAAAC

10. Let’s try another example
INPUT: two strings
OUTPUT: longest common subsequence
ACTGAACTCTGTGCACT
TGACTCAGCACAAAAAC
lcs = TGACTCGCAC
output = 10

11. Brute Force:
For every subsequence of s1, check whether it’s a
subsequence of s2.
s1 has 2m subsequences.
Each subsequence takes Θ(n) time to check: scan s2 for
first letter, for second, and so on.
Time Complexity : Θ(n2m).
m = length of s1
n = length of s2

12. Reccursion
02

13. Alogrithm:
Condition 1: Check if both character arrays are empty. If they are
empty, return 0.
Condition 2: If the character arrays are not empty, then check if the
last character of both character arrays matches or not. If you get a
match, then return 1 + LCS (Both character arrays with reduced size).
Condition 3: If you don’t get a character match, move either one
character in the first character array A or the second character
array B. Pick whichever produces maximum value.

14. Recursion
Tree
let’s consider two string
A = “XY”, length = 2
B = “XPYQ”, length = 4
XY
XPYQ

16. Memoization
(Top down)
03

19. 1.
2.
3.

21. Tabulation
(Bottom up)
04

28. Refrences
Videos
● Abdul Bari
Articles
● Leetcode
● Algotree
● Simplelearn
● TakeUForward

29. CREDITS: This presentation template was created by Slidesgo, and
includes icons by Flaticon and infographics & images by Freepik
Thanks!