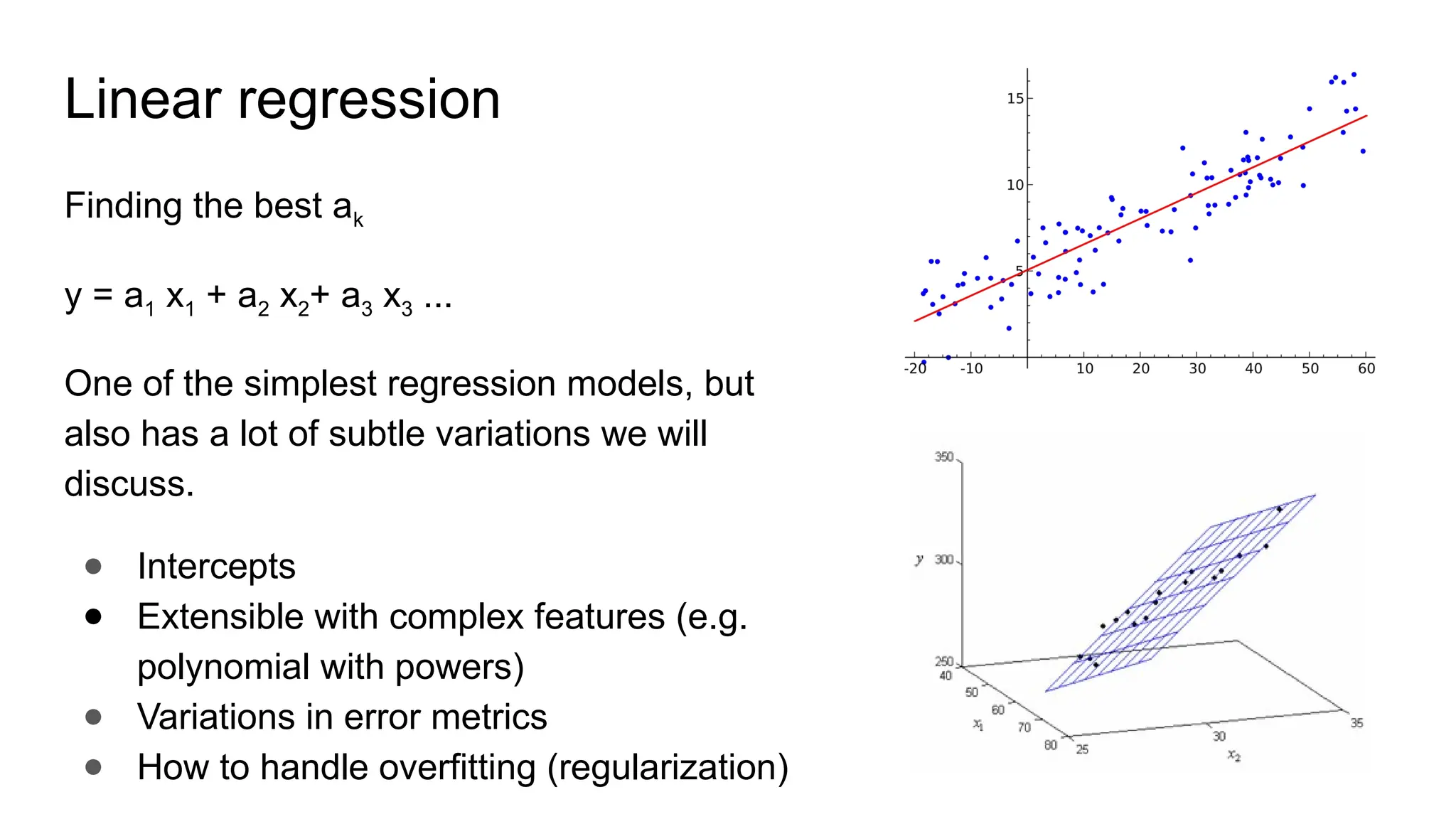
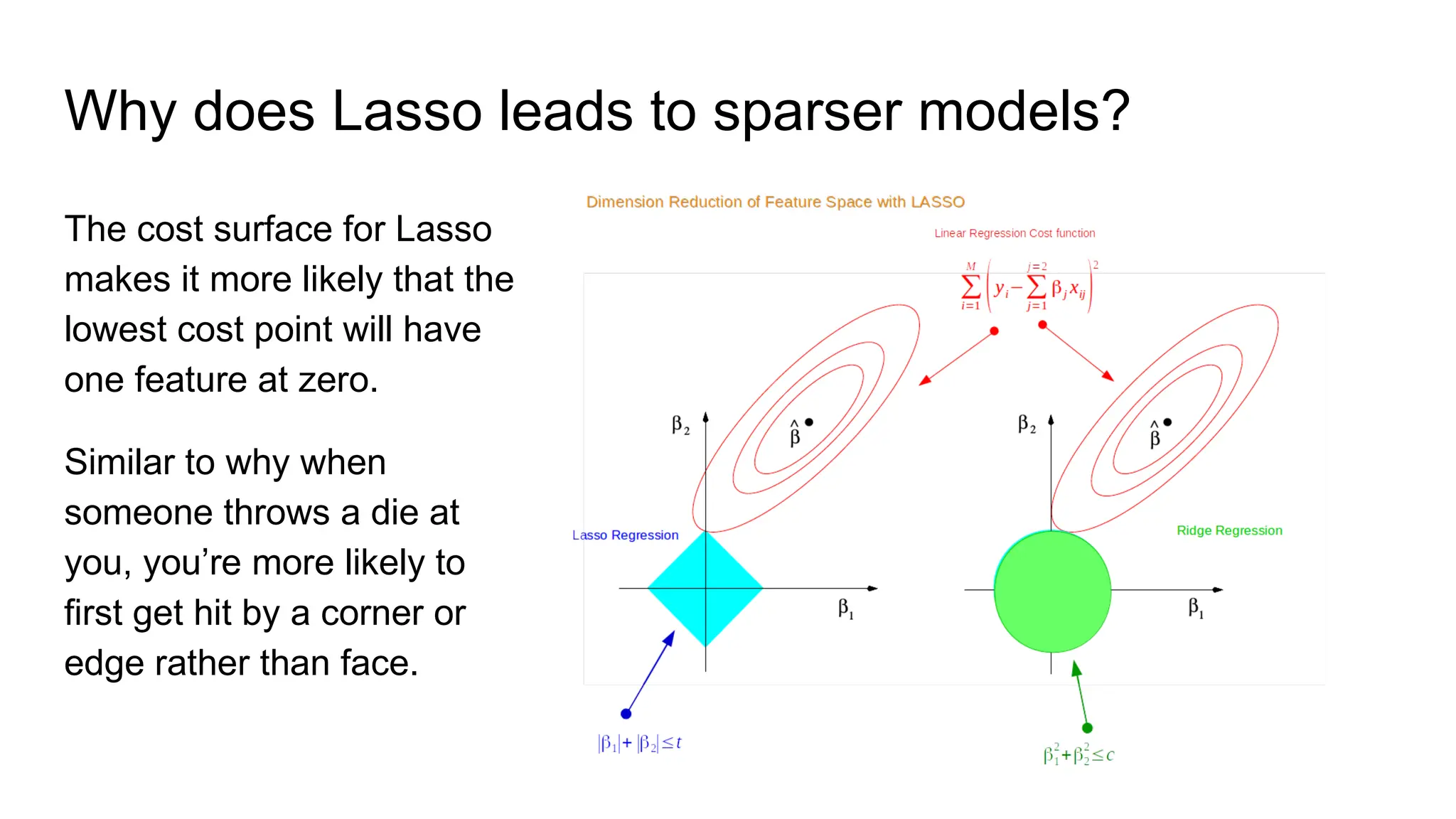
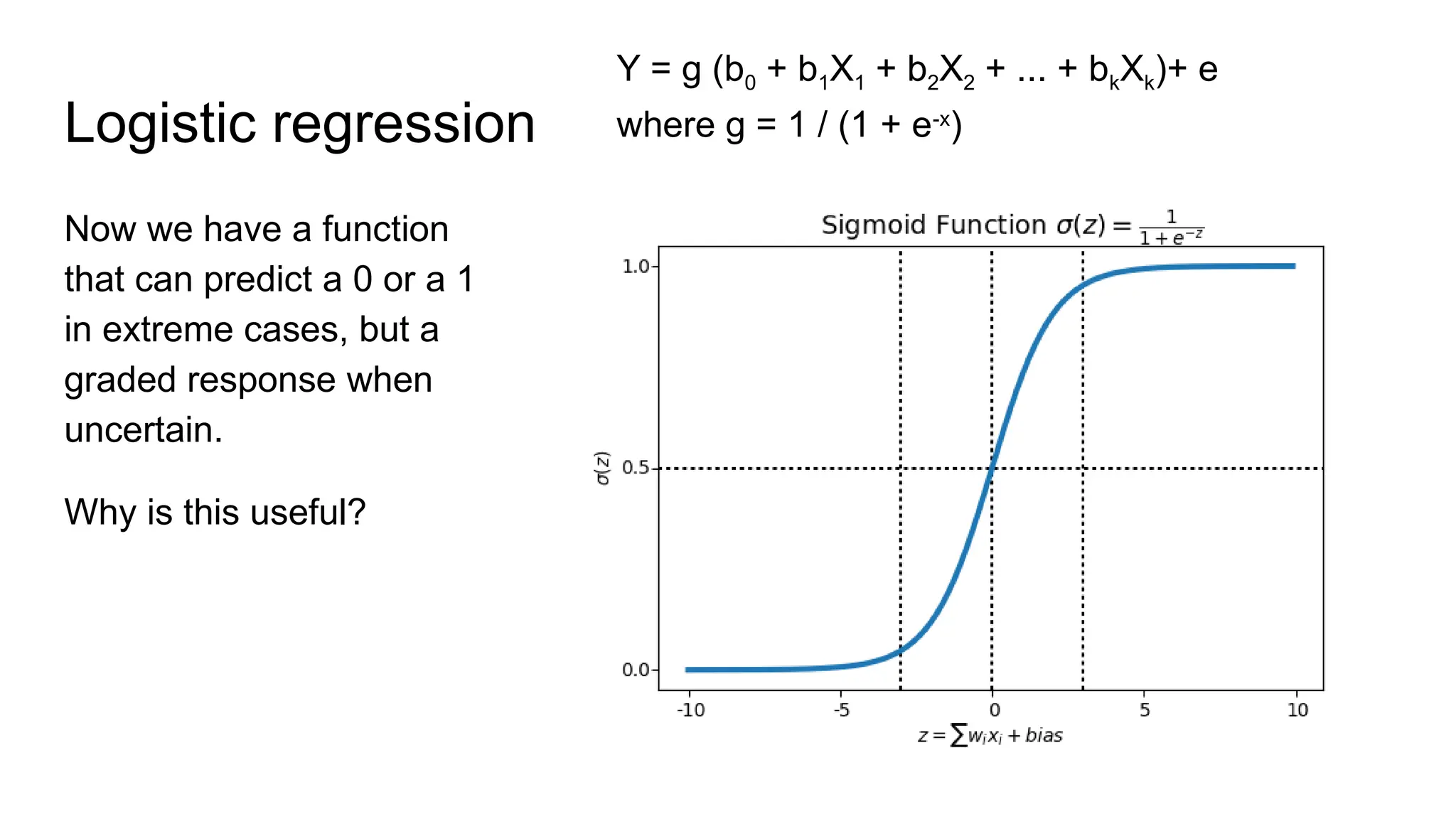
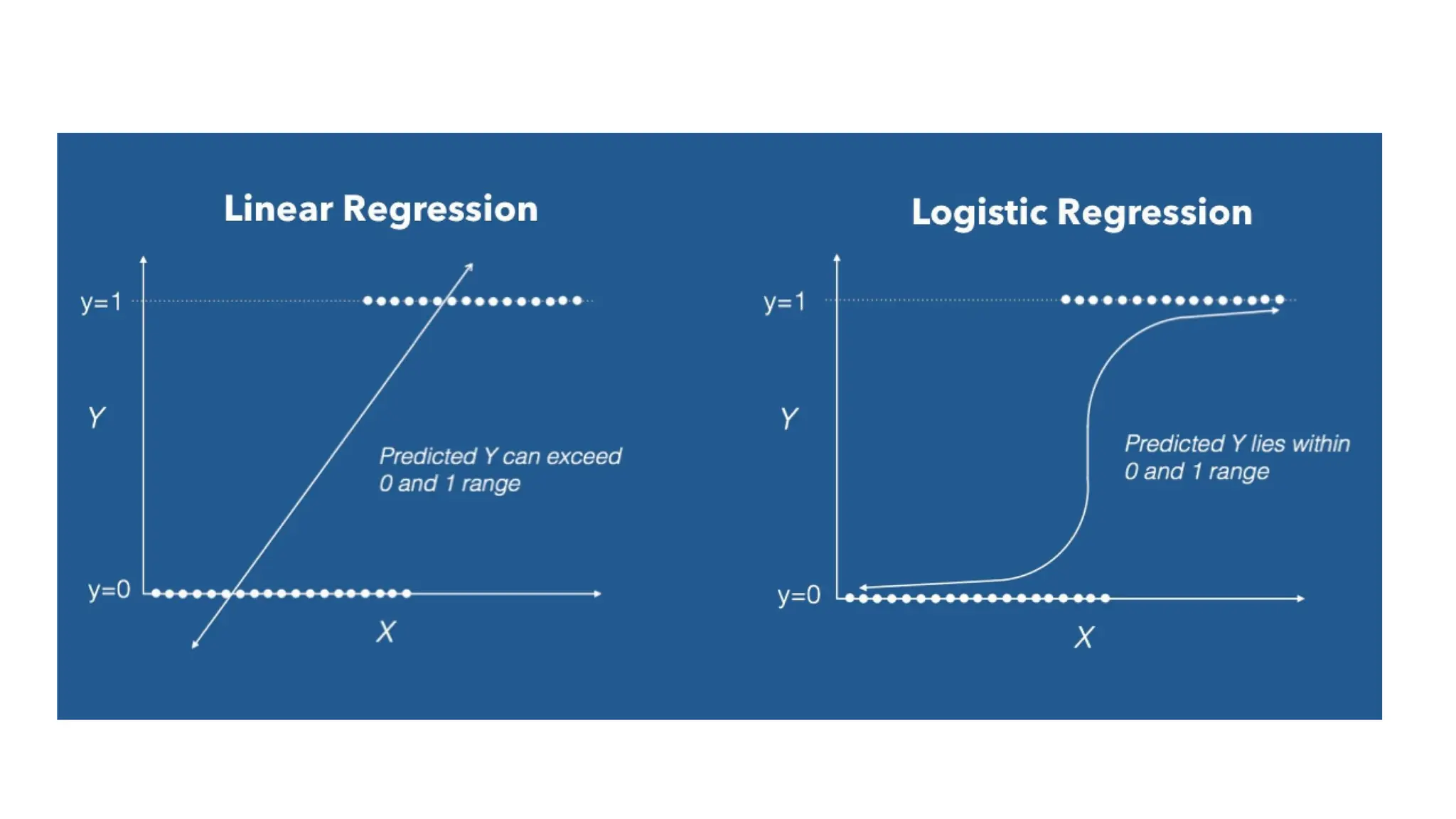
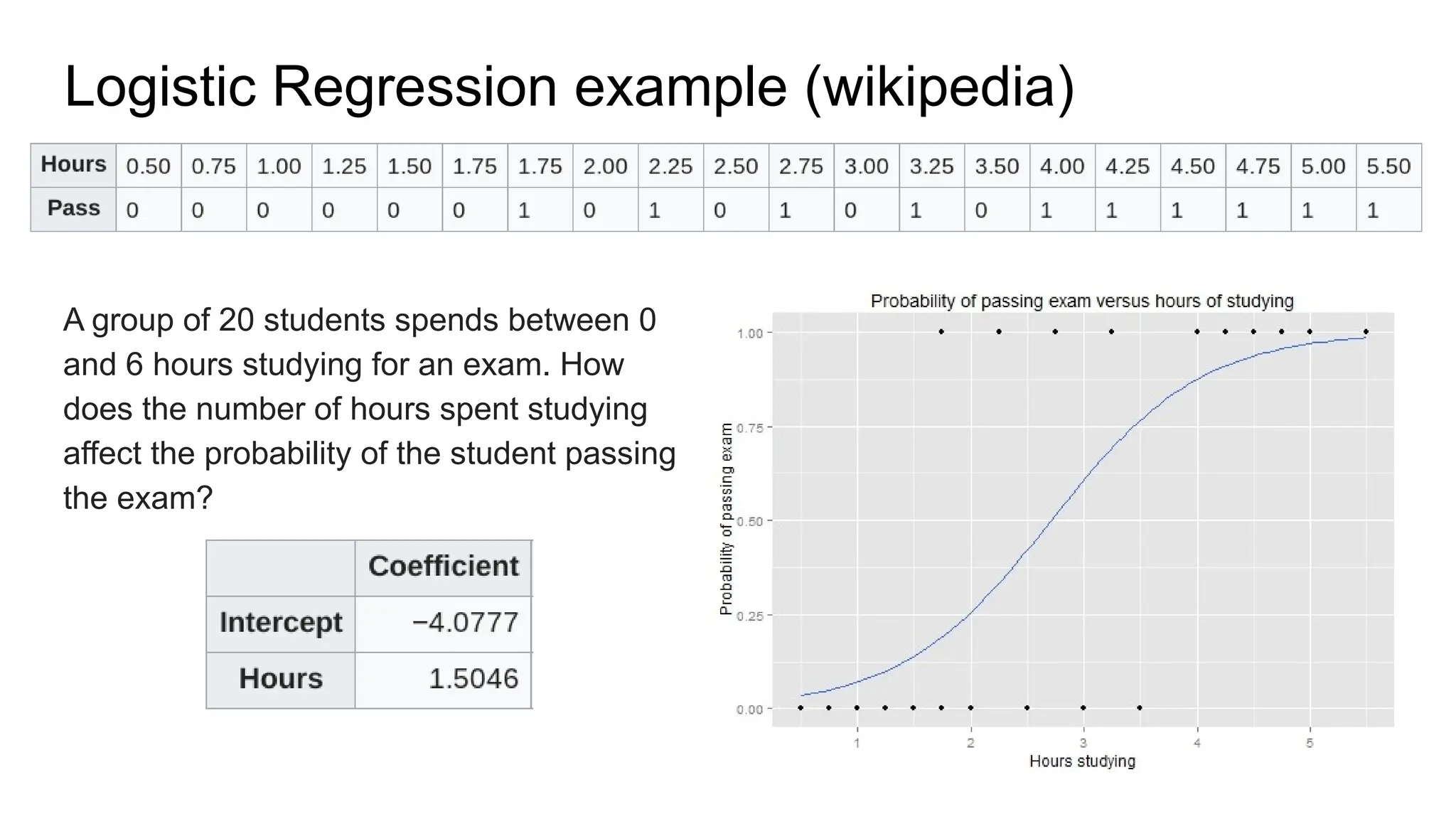
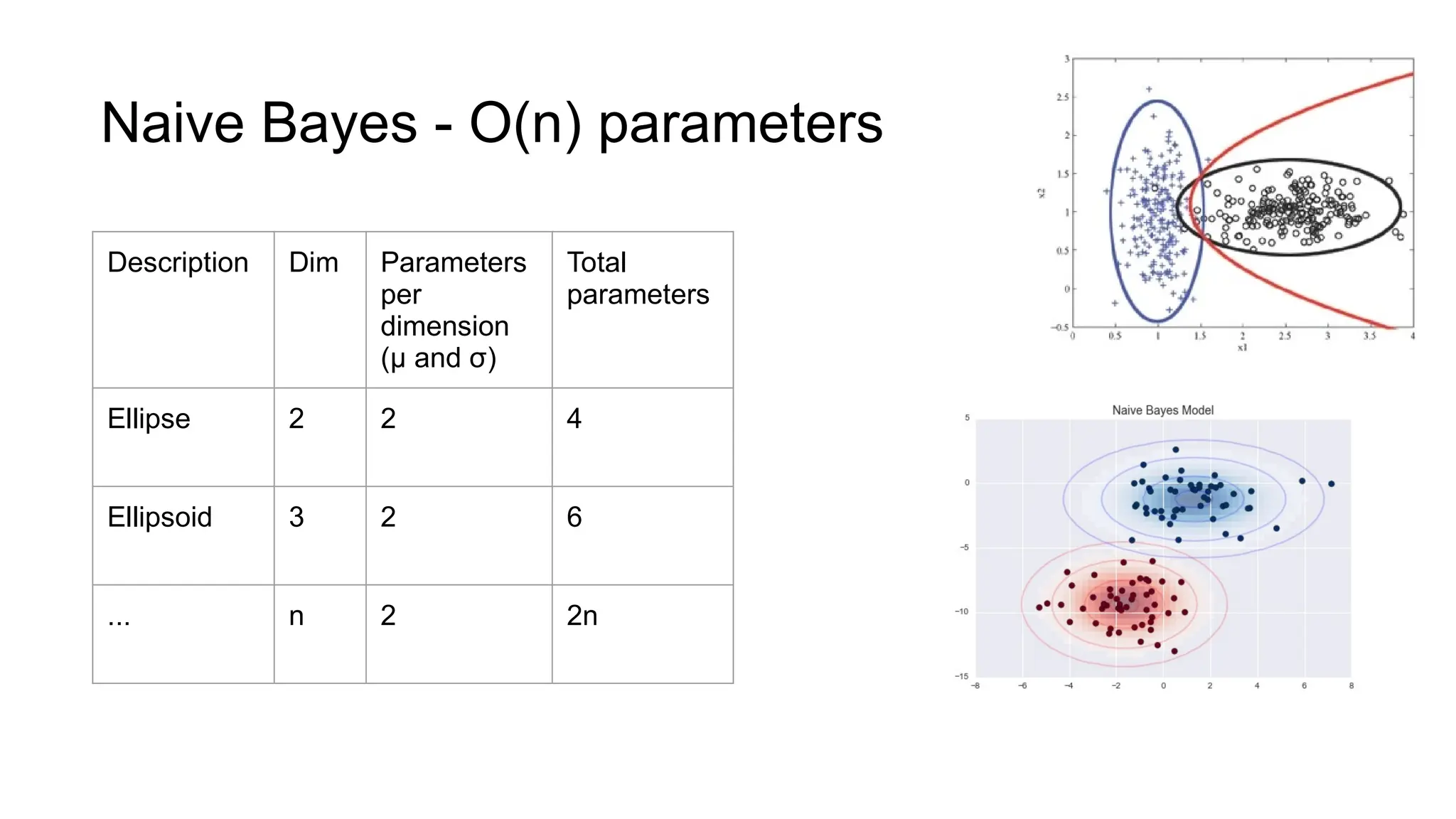
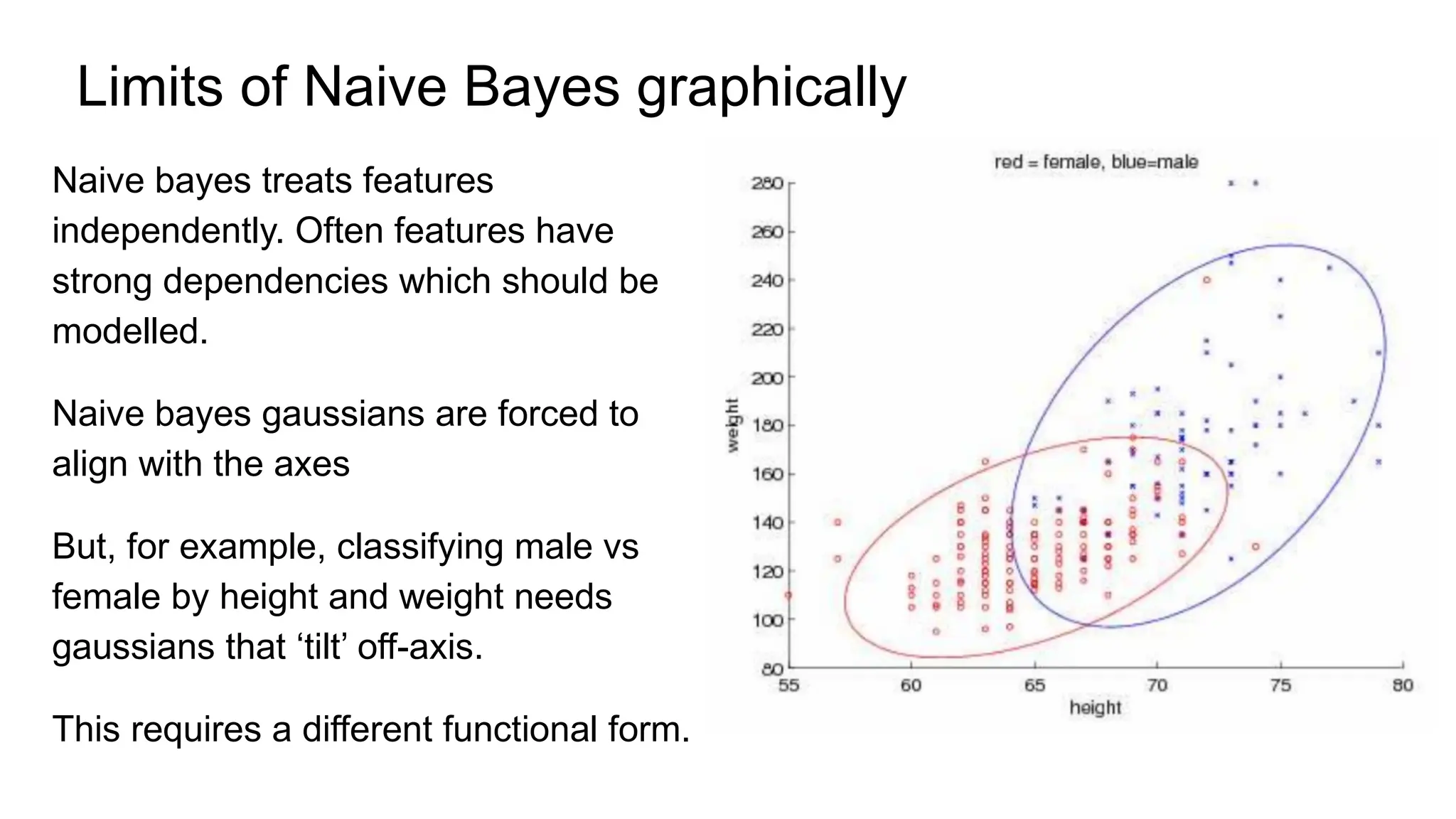
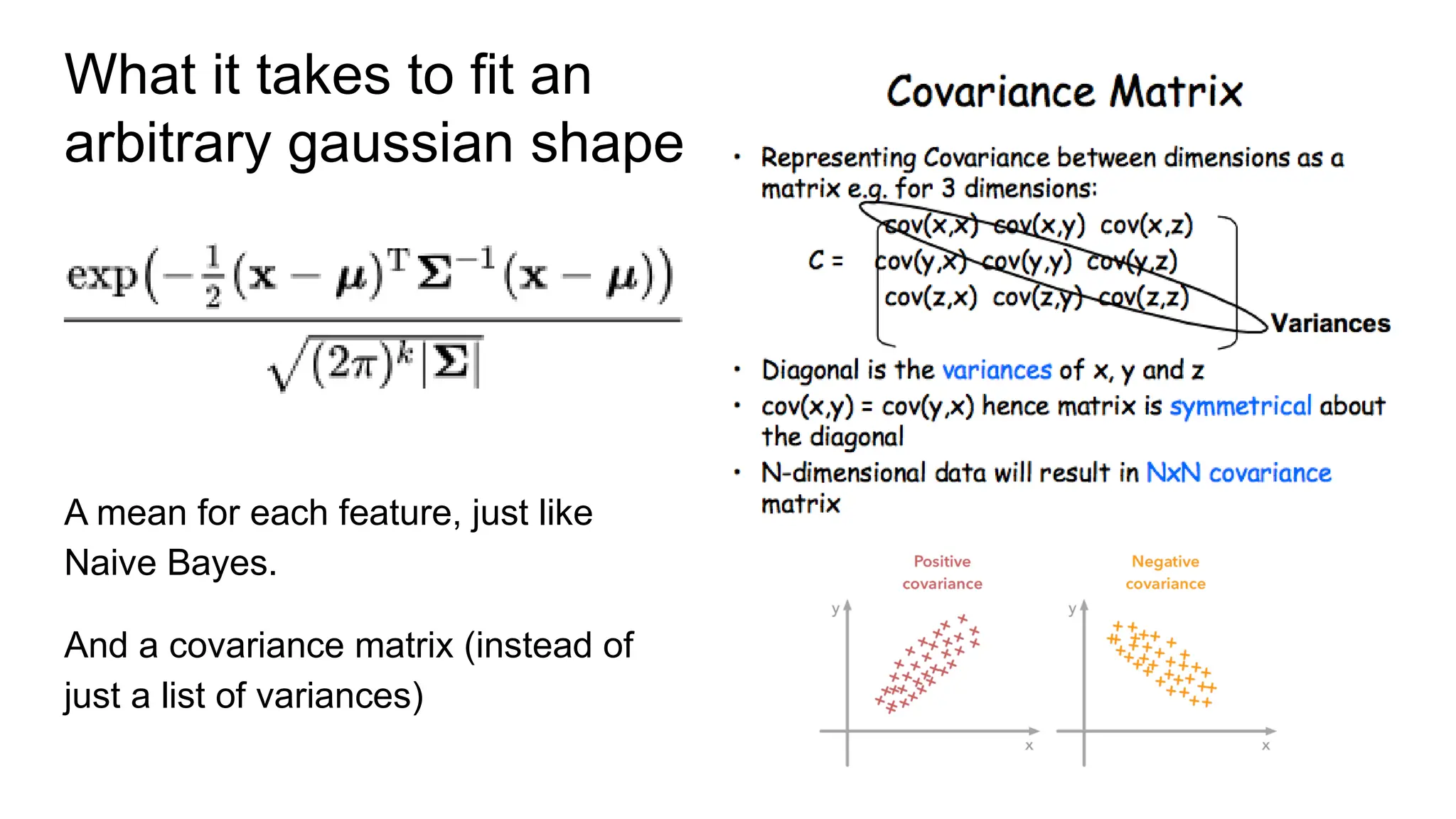
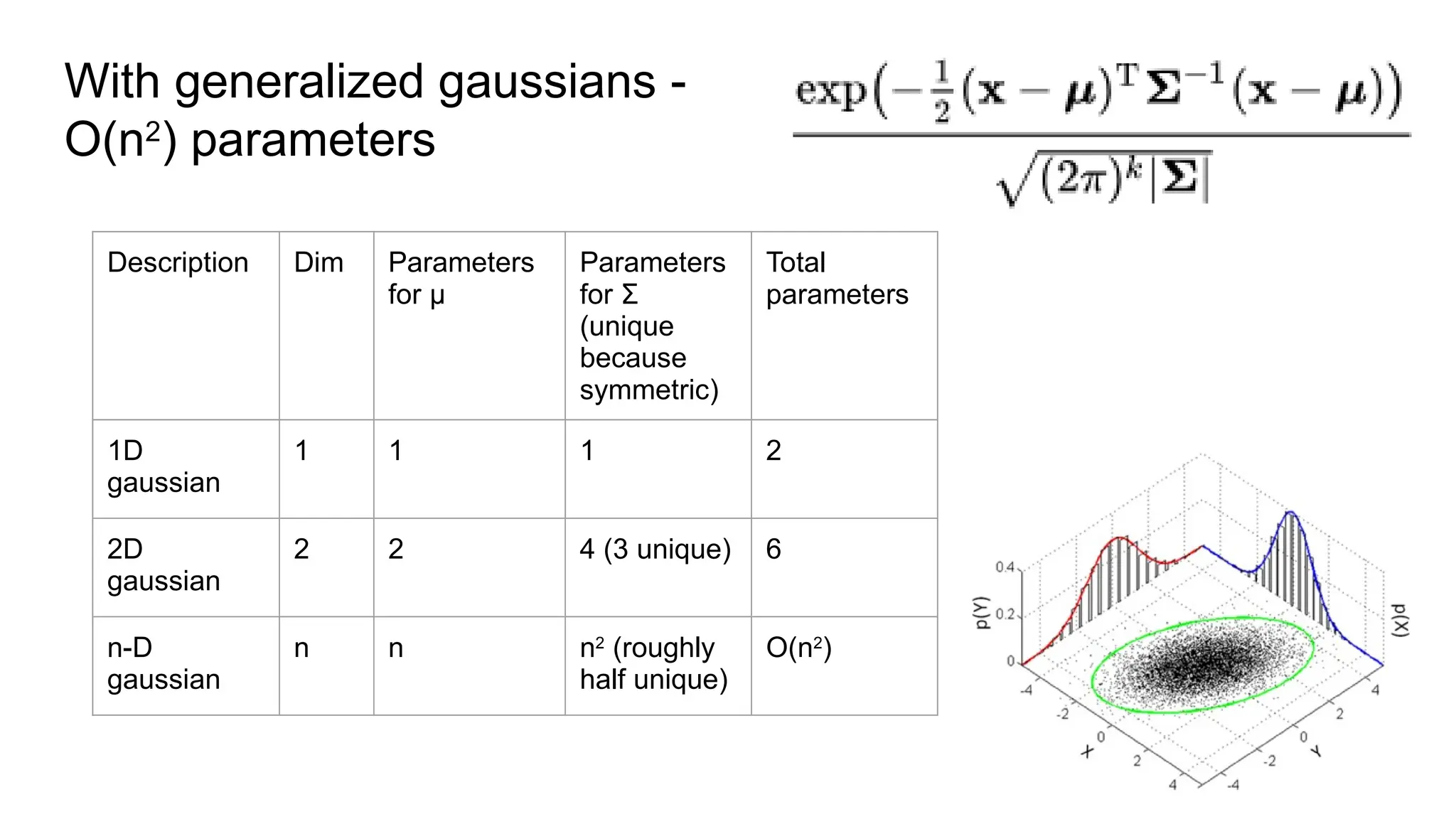
The document discusses various supervised machine learning techniques including k-nearest neighbors, naive Bayes, linear regression, and logistic regression, highlighting their functions, advantages, and applications in predictive modeling. It further elaborates on regularized regression methods such as ridge and lasso, emphasizing their utility in feature selection and handling overfitting. Additionally, the document presents the significance of generalized linear models and the implications of dimensionality in relation to the number of parameters needed for effective learning.

1. Linear regression
Regularized regression and logistic regression

2. Supervised ML, basics
Outline:
● k-NN: intuitive non-parametric classifier
● Naive Bayes: relatively simple parametric
classifier & intro do Bayes terminology
● Linear regression: the simplest regression
model (after k-NN regression)
● Regularized linear regression: introduction
of an extremely powerful hyperparameter

3. Purpose of regression
Succinctly, predicting numbers rather than labels, for example:
● Predicting the severity or strength, rather than presence or absence
○ e.g. how many inches of rain, rather than the presence or absence of rain
● Predicting the future for a quantity of interest
○ Resource allocation for future growth, stock valuation, etc
● Matching a data sample to a known quantity to help interpretation
○ e.g. predicting clinical scores on mobility based on obscure wearable device signals

4. Linear regression
Finding the best ak
y = a1 x1 + a2 x2+ a3 x3 ...
One of the simplest regression models, but
also has a lot of subtle variations we will
discuss.
● Intercepts
● Extensible with complex features (e.g.
polynomial with powers)
● Variations in error metrics
● How to handle overfitting (regularization)

5. Linear regression, more powerful than it may appear
With more complex features, linear regression is arbitrarily powerful
● High frequency trader colleague used regularized linear regression a great
deal, but with complex features
Linear regression can be used to provide a graded classification
○ Binary classification is equivalent to a 0-1 regression with a threshold
○ More on this when discussing logistic regression
○ And multiclass classification can be performed with a one-hot encoding scheme.

6. Ordinary least squares
Minimizing the sum of squares error
advantages: Fast ( O(np2
) where p
is # of features )
disadvantages: includes all features,
even irrelevant ones

7. Ridge regression
Regularization can be used to simplify feature selection within a linear regression
model
Cost is both square error and square of coefficient values.
Note λ = 0: is ordinary linear regression
As λ increases, more feature selection occurs

8. Lasso Regression
Lasso Regression uses the absolute value of the coefficients as the cost. This
creates a sparser set of features (many become zero as λ increases). More useful
for feature selection than Ridge regression.
Disadvantage: requires coordinate descent to fit (vs. Ridge with the same time
complexity as OLS)

9. Why does Lasso leads to sparser models?
The cost surface for Lasso
makes it more likely that the
lowest cost point will have
one feature at zero.
Similar to why when
someone throws a die at
you, you’re more likely to
first get hit by a corner or
edge rather than face.

10. Generalized linear model (GLM) regression
Linear models are strictly of this form
Y = b0 + b1X1 + b2X2 + ... + bkXk
But one problem with this is an infinite range for Y, which sometimes makes little
sense. To fix this, GLMs wrap the linear output in a nonlinear function
Y = g (b0 + b1X1 + b2X2 + ... + bkXk)
Why is that useful? For one version of g, we can force y to be between 0 and 1,
which may make regression useful for classification

11. Logistic regression
Now we have a function
that can predict a 0 or a 1
in extreme cases, but a
graded response when
uncertain.
Why is this useful?
Y = g (b0 + b1X1 + b2X2 + ... + bkXk)+ e
where g = 1 / (1 + e-x
)

13. Logistic Regression example (wikipedia)
A group of 20 students spends between 0
and 6 hours studying for an exam. How
does the number of hours spent studying
affect the probability of the student passing
the exam?

14. Linear regression summary
Ridge and Lasso are types of regularized linear regression
Regularized regression provides a hyperparameter to tune the complexity of the
model through automated feature selection
Recall, it is critical to reduce the number of features
Because n >> (# features)2
for good learning
Lasso produces sparser models, but takes longer to converge (which practically
isn’t much of an issue).
Generalized linear models extend in powerful ways: e.g. logistic regression
Regularized logistic regression is a very powerful classifier and easy to
understand classifier

15. An aside: Why should n > features2
?
Why the rough rule of thumb that the number of samples should be
significantly greater than the number of features squared?
Remember how classification is about grouping similar points in a high
dimensional space (drawing boundaries between those groups)
Most ways of defining groups in n-dimensional spaces require O(n2
) parameters
Let’s try out a few...

16. Rectangles, and hyperrectangles - O(n) parameters
Description Dimens
ions
Parameters
per
boundary
Number of
boundaries
Total
parameters
Rectangle 2 1 4 4
Right rectangular
prism
3 1 6 6
Hyperrectangle n 1 2n 2n

17. Quadrilaterals, Hexahedra, … O(n2
) parameters
Description Dimensions Parameters
per
boundary
Number of
boundaries
Total
parameters
Quadrilateral 2 2 (defines a
line)
4 8
Hexahedron 3 3 (defines a
plane)
6 18
... n n 2n 2n2

18. Naive Bayes - O(n) parameters
Description Dim Parameters
per
dimension
(μ and σ)
Total
parameters
Ellipse 2 2 4
Ellipsoid 3 2 6
... n 2 2n

19. Limits of Naive Bayes graphically
Naive bayes treats features
independently. Often features have
strong dependencies which should be
modelled.
Naive bayes gaussians are forced to
align with the axes
But, for example, classifying male vs
female by height and weight needs
gaussians that ‘tilt’ off-axis.
This requires a different functional form.

20. What it takes to fit an
arbitrary gaussian shape
A mean for each feature, just like
Naive Bayes.
And a covariance matrix (instead of
just a list of variances)

21. With generalized gaussians -
O(n2
) parameters
Description Dim Parameters
for μ
Parameters
for Σ
(unique
because
symmetric)
Total
parameters
1D
gaussian
1 1 1 2
2D
gaussian
2 2 4 (3 unique) 6
n-D
gaussian
n n n2
(roughly
half unique)
O(n2
)

22. To recap on the n > features2
intution...
For arbitrary polyhedra, it takes O(n2
) parameters
For arbitrary gaussians, it takes O(n2
) parameters
…
And there are serious overfitting problems if you have more parameters than you
have samples (note, for linear equations, n samples can generally be fit perfectly
with n features)
But Naive Bayes only needed O(n)? That’s why naive bayes is known to work well
with smaller feature sets, but perform poorly when more data is available.