The document discusses balanced and unbalanced assignment problems and the Hungarian method for solving them. It provides the following key points: - Assignment problems involve assigning jobs to workers or machines to minimize costs or maximize output. The Hungarian method is commonly used to solve them. - Balanced problems have an equal number of jobs and workers, while unbalanced problems have different numbers. 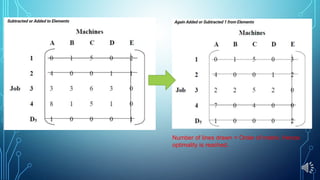- The Hungarian method uses a matrix and steps of row/column reduction, finding minimum uncovered values, and covering zeros with lines to find an optimal assignment. 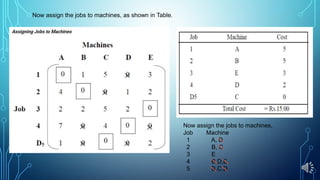- An example shows applying the method to assign four jobs to four machines and minimizing costs in the assignment matrix.

1. ASSIGNMENT
PROBLEM

2. ASSIGNMENT MODEL
• Assigning of jobs to factors (men or machine) to get
most optimum output or get least cost.
• Hungarian method is the mostly used method of
solving assignment problems.
• Types of Assignment problems:
(i) Balanced
(ii) Unbalanced

3. OBJECTIVES
•No workers is more than one job.
•No job is assigned to more than one
worker.
•Total time taken to complete a job is
minimum.
•The work done is cost effective and

4. BALANCED
ASSIGNMENT•An assignment is called
balanced assignment
problem if the number of
persons (factors) is same
as the number of jobs. (number row = number
column)

5. EXAMPLE : Assign the four tasks to four operators.
The assigning costs are given in table.(Minimum
Problem)

6. Step 1: Reduce the matrix by selecting the smallest value in each row and
subtracting from
other values in that corresponding row.
the smallest value:
row A, is 13,row B is 15,row C is 17 and row D is 12.
HUNGARIAN
METHOD

7. HUNGARIAN
METHOD
Step 2: Reduce the new matrix given in the following table by selecting the smallest value in
each column and subtract from other values in that corresponding column.
In column 1, the smallest value is 0, column 2 is 4, column
3 is 3 and column 4 is 0.

8. HUNGARIAN
METHODStep 3: Draw minimum number of lines possible to cover all the zeros in the matrix given in Table
Check whether number of lines drawn is equal to the order of the matrix, i.e., 3 ≠ 4. Therefore
optimally is not reached.

9. HUNGARIAN
METHODStep 4: Take the smallest element of the matrix that is not covered by single line, which is 3. Subtract 3 from
all other values that are not covered and add 3 at the intersection of lines. Leave the values which are
covered by single line.
3
Choose
Smallest
value not
covered line
add 3 at the
intersection
of lines

10. HUNGARIAN
METHODStep 5: Do for row reduction and column reduction again

11. HUNGARIAN
METHODStep 6: Assign the tasks to the operators. Select a row that has a single zero and assign by squaring it.
Strike off remaining zeros if any in that row or column.

12. HUNGARIAN
METHODStep 7: Assign the tasks to the operators.

13. UNBALANCED
ASSIGNMENT•An assignment is called unbalanced assignment
problem if the number of persons (factors) is not
same as the number of jobs. (number row ≠
number column)
(4 rows≠5 columnso unbalanced)

14. Example : A company has five machines that are used for four jobs. Each job
can be assigned to one and only one machine. The cost of each job on each
machine is given in the following table.
Dumm
y Row
5
Dummy Row D5 Added

15. Step 1: Reduce the matrix by selecting the smallest value in each row and
subtracting from
other values in that corresponding row.
HUNGARIAN
METHOD

16. HUNGARIAN
METHOD
Step 2: Reduce the new matrix given in the following table by selecting the smallest value in
each column and subtract from other values in that corresponding column.
Colu
mn
Number of lines drawn ≠ Order of matrix. Hence not
optimal.

17. Select the least uncovered element, i.e., 1, subtract it
from other uncovered elements, add to the elements at
intersection of lines and leave the elements that are
covered with single line unchanged as shown in Table.
Number of lines drawn ≠ Order of matrix. Hence not
optimal.

18. Number of lines drawn = Order of matrix. Hence
optimality is reached.

19. Now assign the jobs to machines, as shown in Table.
Now assign the jobs to machines,
Job Machine
1 A, D
2 B, C
3 E
4 B,D,E
5 B,C,D

20. THANK YOU