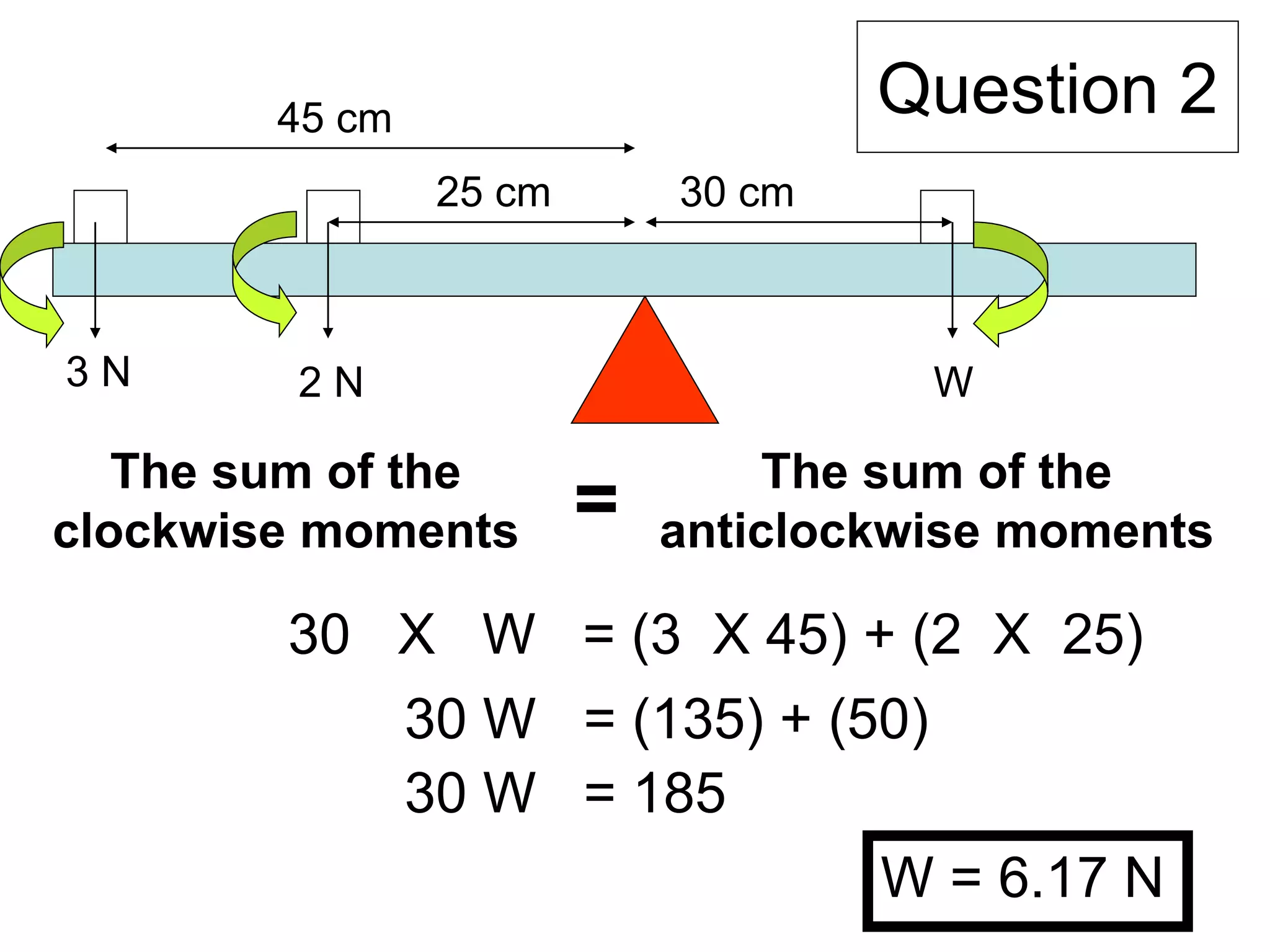
The document explains the concept of moments in physics, specifically defining a moment as the product of force and perpendicular distance from a pivot. It discusses the principle of moments, which states that for a body in equilibrium, the total clockwise moments must equal the total anticlockwise moments. Additionally, it illustrates calculations related to finding unknown forces and distances based on balancing moments.

1. Specification
Moment of a force about a point.
Moment defined as force × perpendicular distance from the point to the line of action of
the force.
Principle of moments.
Moments

2. 2 of 26 © Boardworks Ltd 2009
Forces can make things accelerate. They can also make
things rotate.
What’s wrong with these pictures?
We know instinctively that we need to apply a force at a large
distance from the pivot for it to be effective.
too
short!
too
short!
wrong
place!
Introduction to turning forces

3. 3 of 26 © Boardworks Ltd 2009
Equilibrium
A body persists in equilibrium if no net force or
moment acts on it. Forces and moments are balanced.
Newton’s first law states that a body persists in its state of
rest or of uniform motion unless acted upon by an external
unbalanced force.
Bodies in equilibrium are therefore bodies that are at rest or
moving at constant velocity (uniform motion).
F1
F1
F2 F2
equilibrium

4. 4 of 26 © Boardworks Ltd 2009
4m 2m
If the total clockwise moment on an object is balanced by the
total anticlockwise moment, then the object will not rotate.
Provided that there are no other unbalanced forces on it, the
object will be in equilibrium, like the beam below:
3N 6N
total anticlockwise moments = total clockwise moments
3 × 4 = 6 × 2
12Nm = 12Nm
Balanced moments

5. 5 of 26 © Boardworks Ltd 2009
The principle of moments
The principle of moments states that (for a body in
equilibrium):
total clockwise
moments
=
total anticlockwise
moments
4N 6N
5m d
4 × 5 = 6d
This principle can be used in calculations:
What is d?
20 = 6d
d = 20 / 6
d = 3.3m

6. Question 1
200N x
1.2 m 0.8 m
The sum of the
clockwise moments
The sum of the
anticlockwise moments
=
0.8 X x = 1.2 X 200
0.8 X x = 240
x = 240
0.8 300 N

7. Question 2
2 N W
25 cm 30 cm
45 cm
3 N
The sum of the
clockwise moments
The sum of the
anticlockwise moments
=
30 X W = (3 X 45) + (2 X 25)
30 W = (135) + (50)
30 W = 185
W = 6.17 N

8. Question 3
3 N 6.17 N
25 cm x
45 cm
2 N
The sum of the
clockwise moments
The sum of the
anticlockwise moments
=
x X 6.17 = (2 X 45) + (3 X 25)
6.17x = (90) + (75)
6.17x = 165
26.7 cm

9. Question 4
The sum of the
clockwise moments
The sum of the
anticlockwise moments
=
240 mm
4.5 N
W
160 mm
4.5 X 240 = W X 160
1080 = 160 W
1080 = W
160 6.75 N

10. normal reaction
100N W

11. sum of anticlockwise moments = sum of clockwise moments
43.2 = 0.4 x 100 + 0.55 x W
43.2 = 40 + 0.55W
W = 5.8 N
Moment = perpendicular distance x force
= 1.20 x 36
= 43.2Nm

12. When a body is in equilibrium, the net moment acting on it is zero:
Sum of clockwise moment(s) = sum of anticlockwise moment(s)

13. weight
of child
weight
of plank
178N
d

14. 429 N
149 N
178 N
weight of child
429 +149 = 179 +W
400 N
d x 400 + 2.5 x 178 = 5 x 149
400d +445 = 745
400d = 745 – 445
400d = 300
d = 300/400
0.75 m