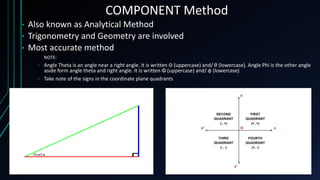
This document discusses scalar and vector quantities. Scalars have magnitude but no direction, and include things like temperature, mass, and time. Vectors have both magnitude and direction, such as force, velocity, and electric field. There are two methods for adding vectors: the head-to-tail method involves drawing vectors end to end to form a polygon, and the component method breaks vectors into their x and y components, which are added separately to find the resultant vector. Both methods produce the same final summed vector.

1. VECTORS
SCALAR AND VECTORS

2. • SCALAR
• Temperature – Celsius, Kelvin
• Pressure - mmHg
• Length – cm, m, km, yards, feet,
inches
• Energy – calories, horsepower per
hour, thermies, etc
• Mass – g, kg, ton, pound, etc
• Time – or duration - seconds,
minutes, hours
• Area – square meters (m2)
• Volume – cubic centimeters (cm2)
• Frequency – hertz (Hz)
• Density – kilograms per cubic
meter (kg / m3)
• VECTOR
• Weight – gravitational attraction
• Force – expressed in N
• Acceleration –speed over time
• Speed – meters per second
• Torsion – or torque – change of
direction of a vector towards a
curvature
• Position
• Voltage – path of the charge
between starting and end point
• Electric field
• Gravitational field
• Inertia – force of friction

3. Mini Activity:
• Based on the list of units above, what do you think is the main
difference of Scalar quantity and Vector quantity?

4. VECTORS
ADDING VECTORS

6. There are 2 ways in adding
Vectors:
• HEAD – TO – TAIL METHOD
• COMPONENT METHOD
The sum of vectors is called
Resultant Vector or R or R with
direction

7. HEAD – to – TAIL Method
• Also known as TAIL – to – TIP and POLYGON
Method
• Simplest way in adding vectors
• STEPS:
1. Using a graphing paper, ruler, and protractor, draw the first
vector
2. Draw the second vector, such that its tail connects to the head
or tip of the first vector
3. Connect where you ended on your second vector, to the starting
point
4. Manually measure your Resultant Vector
NOTE: Use protractors correctly in graphing angles.

8. COMPONENT Method
• Also known as Analytical Method
• Trigonometry and Geometry are involved
• Most accurate method
NOTE:
• Angle Theta is an angle near a right angle. It is written Θ (uppercase) and/ θ (lowercase). Angle Phi is the other angle
aside form angle theta and right angle. It is written Φ (uppercase) and/ φ (lowercase)
• Take note of the signs in the coordinate plane quadrants

9. 1. Using a graphing paper and a ruler, draw the first vector (v1). The starting point is the zero of the coordinate plane
quadrant.
• A right triangle is formed once plotted, making the vector - the side opposite of the right angle or the
hypotenuse. The other side of the Θ angle in coordination with the x or y axis is the adjacent, and the
remaining side is the opposite.
2. Calculate the x components and y components of v1, noting the angle given as Θ.
• Once the parts of the triangles are determined, we will use SOH CAH TOA for the Θ angle . The line that is in
coordinate with the X - axis (use cos Θ) is the V X. The line that is in coordinate with the Y – axis (use sin Θ) is
the V Y.
V X1 = v cos Θ V Y1 = v sin Θ
3. Draw the second vector (v2). The starting point is the zero of the coordinate plane quadrant.
• A right triangle is formed once plotted, making the vector - the side opposite of the right angle or the
hypotenuse. The other side of the Θ angle in coordination with the x or y axis is the adjacent, and the
remaining side is the opposite.
4. Calculate the x components and y components of v2, noting the angle given as Θ.
• Once the parts of the triangles are determined, we will use SOH CAH TOA for the Θ angle . The line that is in
coordinate with the X - axis (use cos Θ) is the V X. The line that is in coordinate with the Y - axis (use sin Θ) is
the V Y.
V X2 = v cos Θ V Y2 = v sin Θ
5. Add the ALL horizontal or x components of the vectors to get the Resultant component of X ( ∑ V X or R X ). Add the
ALL vertical or y components of the vectors to get the Resultant component of Y ( ∑ V Y or R Y)..
• BE CAREFUL with the signs. Right and Up – POSITIVE, Left and Down – NEGATIVE
R X = V X1 + V X2 + V X3 . . . R Y = V Y1 + V Y2 + V Y3 . . .
6. Use the Pythagorean Theorem to get Resultant Vector of Resultant component of X or R X and of Resultant
component of Y or R Y .
R = √ R X
2 + R Y
2
STEPS

10. To get the direction of the Resultant:
Note: use a scientific calculator
• Make it on its absolute value, then write the degree sign.
• To specifically recognize whether it is North – East, North –
West, South – East, or South – West, base the direction
from your R X andR Y.