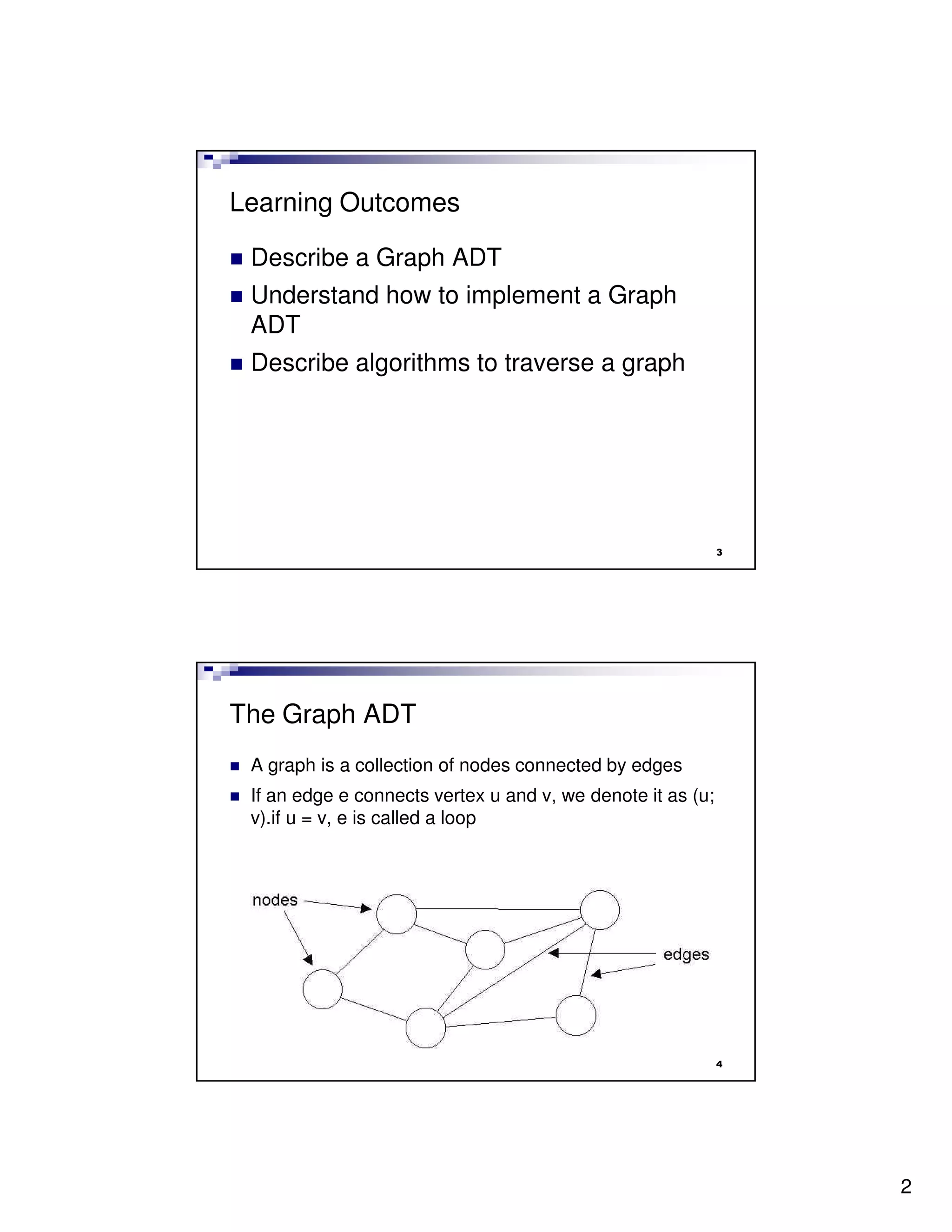
This document outlines key concepts about graph data structures including: - Graphs consist of nodes connected by edges - Graphs can be directed or undirected - Common operations on graphs include adding/removing nodes/edges and checking connections - Graph traversals involve starting at a node and processing neighbors until all reachable nodes are processed - Graphs can model real-world problems like computer networks

1. Lecture 8
Graph
Data Structure (CS221)
Abdisalam Issa-Salwe
Taibah University
College of Computer Science & Engineering
Computer Science Department
Outline
Graph Data Type
Graph Concepts
Graph Data Structure
Directed/undirected Graph
Graph Relationship
Graph implementation
2
1

2. Learning Outcomes
Describe a Graph ADT
Understand how to implement a Graph
ADT
Describe algorithms to traverse a graph
3
The Graph ADT
A graph is a collection of nodes connected by edges
If an edge e connects vertex u and v, we denote it as (u;
v).if u = v, e is called a loop
4
2

3. Graph Concepts
A tree is an example of a graph
In a graph a node may be it’s own
ancestor
In general a graph has no root node
Formally, a graph is an ordered pair of
sets (N,E)
Both nodes and edges may have data
values associated
5
Graph Data Structure (cont…)
Graph is a data structure that consists of a set of
nodes and a set of edges that relate the nodes
to one another
It is made up of a set of nodes called vertices
and a set of lines called edges (or arcs) that
connect the nodes.
If the edges in the graph have no direction it is
called an undirected graph.
A graph whose edges are directed from one
vertex to another is called a directed graph, or
digraph
6
3

4. Graphs Data Structure (cont…)
More definition:
• Like a tree, is a NON-Linear structure
consisting of nodes and links between
the nodes
Types: Undirected graph
Directed graph
Graphs are often used to solve problems
7
Undirected Graph
• An undirected graph is a set of nodes
and a set of links between the nodes.
• Each NODE is called a VERTEX
V0 V1
• Each LINK is called an EDGE E0
• The order of the two connected vertices
is unimportant
ex: whether “V0 connects V1” or
“V1 connects V0”
means the same thing
8
4

5. Undirected Graph examples
5 vertices
6 edges
V0
E0 E1 V2 E5
V1 E4
E2 V4
V3 E3
9
Undirected Graph examples
5 vertices 6 edges
V3 E4
V2
E2 E1 E0 V0
V1
E3 V4 E5
In drawing, the placement of the vertices
is UNIMPORTANT same as previous graph
10
5

6. Directed Graph
A directed graph is a finite set of vertices
together with a finite set of edges. If both
are empty then we have an empty graph
V1 SOURCE V0
V2
V1
V4
V3 TARGET V3
11
Directed Graph
• Loops: a loop connects a vertex to itself
LOOP
Vertex
• Path: is a sequence of vertices
P0, P1, P2,… Pn , each adjacent pairs of
vertices Pi and Pi+1 are connected by an edge
path
V1 V3
SOURCE TARGET
12
6

7. Directed Graph
• Multiple edges:
a graph may have two or more edges
connecting the same two vertices in the same
direction
Directed
Undirected
V0
V0
V2
V2 V1
V1
V4
V3
V3 V4 13
Directed Graph
• Simple graph:
• No loops
• No multiple edges
• Directed
• Undirected
• Directed graph representation:
• Using a 2-Dim array
• Using a Linked List for each vertex
• Using the set class from the C++
Standard Library ( edge sets )
14
7

8. Graph Relationship
Adjacent vertices: Two vertices in a
graph that are connected by an edge
Path: A sequence of vertices that
connects two nodes in a graph
Complete graph: A graph in which every
vertex is directly connected to every other
vertex
Weighted graph: A graph in which each
edge carries a value
15
Graph Relationship (cont…)
In a complete graph, every vertex is
adjacent to every other vertex.
If there are N vertices, there will be N * (N
- 1) edges in a complete directed graph
and N * (N - 1) / 2 edges in a complete
undirected graph.
16
8

9. Weighted graphs can be used to represent
Weighted graph applications in which the value of the
connection between the vertices is important,
not just the existence of a connection.
17
Complete graph
18
9

10. Degree
In an undirected graph, the degree of a
vertex u is the number of edges connected
to u.
In a directed graph, the out-degree of a
vertex u is the number edges leaving u,
and its in-degree is the number of edges
ending at u
Each vertex is associated with a linked list
that enumerates all the vertices that are
connected to u
19
Graph Traversals (cont…)
In general:
•Both traversal algorithms
1. Start at one vertex of a graph
2. Process the information contained
at that vertex
3. Move along an edge to process a
neighbor
20
10

11. Graph Traversals (cont…)
• The traversal algorithm should be
careful that it doesn’t enter a “Repetitive
Cycle”. Therefore we will mark each vertex as
it is processed..
• When the traversal finishes, all of the vertices
that can be reached from the start vertex have
been processed.
• Some of the vertices may not be processed
because there is NO PATH from the START
VERTEX 21
Solving a simple problem using a graph
A network of computers can be represented
By a graph, with
• each vertex representing One of the
machines in the network, and
• an Edge representing a communication wire
Between the two machines.
The question of whether one machine can send
a message to another machine boils down to
whether the corresponding vertices are
Connected by a path
22
11

12. Solving a simple problem using a graph
V0 6
1 V0 to V3 = 1
3 V1
V3
V3 to V1 = 3
2 V1 to V2 = 2
7
V2 Total 6
6
• Each edge has a NON-Negative Integer value
attached to it called the weight or cost of the edge
The path with the lowest cost is called the
Shortest path
23
Node ADT
Essential Operations
create: Element → Node
changeElement: Node´Element → Node
getElement: Node → Element
24
12

13. Edge ADT
Essential Operations
• create: Node´Node´Attribute → Edge
• changeAttribute: Edge´Attribute → Edge
• getAttribute: Edge → Attribute
• getNodes: Edge → Node´Node
• getEdge: Node´Node → Edge
25
Digraph ADT
create: → Graph
addNode: Node´Graph → Graph
addEdge: Edge´Graph → Graph
containsNode: Node´Graph → Boolean
containsEdge: Node´Node´Graph → Boolean
removeNode: Node´Graph → Graph
removeEdge: Node´Node´Graph → Graph
numNodes: Graph → Integer
numEdges: Graph → Integer
26
13

14. Digraph ADT
Other helpful operations
an iterator over all nodes in the graph;
an iterator over all edges in the graph;
for each node, an iterator over all nodes to
which it has an edge.
27
Digraph Implementations
Edge Set implementation
Set of Nodes
Set of Edges - (node, node, attribute)
Standard method of representing sets
e.g. hash table, BSTree
28
14

15. Digraph Implementations (cont…)
Adjacency Set (or Adjacency List)
implementation
Set of Nodes
Data at each node includes list of adjacent
nodes and edge attributes
Standard method of representing sets
e.g. hash table, BSTree
29
15