This document provides an overview of adaptive filters and their design using MATLAB. It discusses linear filters, optimal filter design methods, the Wiener filter, adaptive filters, the LMS adaptive algorithm and its stability, applications of adaptive filters including system identification, equalization, prediction and interference cancellation. It also presents a novel adaptive IIR notch filter for frequency estimation and tracking of harmonic signals, describing its structure, transfer function and performance. References are provided for further reading.

1. Content Beyond Syllabi
EE8591 Digital signal processing
Adaptive Filters & Filter design using MATLAB
Dr. N.G.P. INSTITUTE OF TECHNOLOGY
Au Autonomous Institution
Approved by AICTE, New Delhi, Affiliated to Anna University, Chennai,
Recognized by UGC & Accredited by NAAC and NBA (BME, CSE, ECE, EEE &Mechanical)
DEPARTMENT OF ELECTRICAL AND ELECTRONICS ENGINEERING

2. 2
introduction
Linear filters :
the filter output is a linear function of the filter input
Design methods:
• 1 The classical approach
frequency-selective filters such as
lowpass / bandpass / notch filters etc
• 2 Optimal filter design
Mostly based on minimizing the mean-square value
of the error signal [1]

3. 3
Wiener filter
• work of Wiener in 1942 and Kolmogorov in 1939
• it is based on a priori
statistical information
• when such a priori
information is not available,
which is usually the case,
it is not possible to design
a Wiener filter in the first
place
[1]

4. 4
Adaptive filter
• the signal and/or noise characteristics are often
nonstationary and the statistical parameters vary
with time
• An adaptive filter has an adaptation algorithm, that is
meant to monitor the environment and vary the filter
transfer function accordingly
• based in the actual signals received, attempts to find
the optimum filter design [1]

5. 5
Adaptive filter
• In a stationary environment, the filter is expected to
converge, to the Wiener filter
• In a nonstationary environment,
the filter is expected to
track time variations and
vary its filter coefficients
accordingly
[1]

6. 6
Adaptive filter
• The basic operation now involves two
processes :
1. a filtering process, which produces an output signal
in response to a given input signal.
2. an adaptation process, which aims to adjust the
filter parameters (filter transfer function) to the
(possibly time-varying) environment
Often, the (avarage) square value of the error signal
is used as the optimization criterion
[1]

7. 7
Adaptive filter
• Because of complexity of the optimizing algorithms
most adaptive filters are digital filters that perform
digital signal processing
• When processing
analog signals,
the adaptive filter
is then preceded
by A/D and D/A
convertors. [1]

8. 8
Adaptive filter
• The generalization to adaptive IIR filters leads to
stability problems
• It’s common to use
a FIR digital filter
with adjustable
coefficients.
[1]

9. 9
LMS Algorithm
• Most popular adaptation algorithm is LMS
Define cost function as mean-squared error
• Based on the method of steepest descent
Move towards the minimum on the error surface to
get to minimum
gradient of the error surface estimated at every
iteration

















 
































signal
error
vector
input
tap
parameter
rate
-
learning
vector
weight
-
tap
of
value
old
vector
weigth
-
tap
of
value
update
[2]

10. 10
LMS Algorithm
)
(
)
(
2
)
(
)
1
(
)
(
)
(
2
)
(
)
(
)
(
2
)
(
)
(
)
(
)
(
)
(
2
)
(
)
(
2
)
(
),
(
)
(
)
1
(
)
(
ˆ
)
(
)
(
)
(
)]
(
),...,
1
(
),
(
[
)
(
],
,...,
,
[
)
(
2
2
1
0
)
(
)
(
)
(
2
2
2
1
0
n
X
n
e
n
W
n
W
n
X
n
e
n
e
i
n
x
n
e
W
n
e
i
n
x
n
W
y
W
n
y
n
e
W
n
e
n
e
W
n
e
StepSize
n
e
n
W
n
W
n
e
n
y
n
d
n
e
N
n
x
n
x
n
x
n
X
w
w
w
n
W
i
N
i
i
n
y
n
d
n
e
i
i
N


























 























[2]

11. 11
Stability of LMS
• The LMS algorithm is convergent in the mean square
if and only if the step-size parameter satisfy
• Here max is the largest eigenvalue of the correlation
matrix of the input data
• More practical test for stability is
• Larger values for step size
– Increases adaptation rate (faster adaptation)
– Increases residual mean-squared error
max
2
0




power
signal
input
2
0 


[2]

12. 12
Applications of Adaptive Filters:
Identification
• Used to provide a linear model of an unknown plant
• Applications:
– System identification [2]

13. 13
Applications of Adaptive Filters:
Inverse Modeling
• Used to provide an inverse model of an unknown
plant
• Applications:
– Equalization (communications channels)
[2]

14. 14
Applications of Adaptive Filters:
Prediction
• Used to provide a prediction of the present value of a
random signal
• Applications:
– Linear predictive coding
[2]

15. 15
Applications of Adaptive Filters:
Interference Cancellation
• Used to cancel unknown interference from a primary
signal
• Applications:
– Echo / Noise cancellation
hands-free carphone, aircraft headphones etc [2]

16. 16
Example:
Acoustic Echo Cancellation
[1]

17. 17
A new work
• Novel Adaptive IIR Filter for Frequency
Estimation and Tracking
In many applications we may want to estimate (track)
the signal’s fundamental frequency as well as any
harmonic frequencies
In this article, we present a novel adaptive harmonic IIR
notch filter with a single adaptive coefficient to
efficiently perform frequency estimation and tracking
in a harmonic frequency environment [3]

18. 18
Structure
frequency estimation of a measured signal x(n)
V(n) is a white Gaussian noise
• To estimate frequency in such a harmonic frequency
environment, a IIR notch filter presented for the
case of M=3 (the fundamental and
two harmonics)
[3]

19. 19
Pole zero plot
• Parameter r is chosen to be close to, but less than,
one to achieve narrowband notches and avoid any
filter stability problems [3]

20. 20
Transfer function
• the transfer function has only one adaptive coefficient
• Our objective, then, is to minimize the power of the
last subfilter output
[3]

21. 21
MSE
• we could determine a frequency capture range based
on the plotted MSE function [3]

22. 22
Performance
[3]

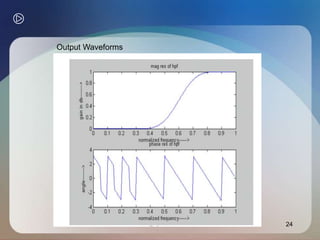
23. 23
PROGRAM: HIGH PASS FIR FILTER DESIGN USING WINDOW METHOD
clc; clear all;
close all;
n=20;
fp=300; f
q=200;
fs=1000;
fn=2*fp/fs;
window=blackman(n+1);
b=fir1(n,fn,'high',window);
[H W]=freqz(b,1,128);
subplot(2,1,1);
plot(W/pi,abs(H));
title('mag res of hpf’);
ylabel('gain in db-------->’);
xlabel('normalized frequency------>’);
subplot(2,1,2); plot(W/pi,angle(H));
title('phase res of lpf'); ylabel('angle-------->’);
xlabel('normalized frequency------>')

24. 24
Output Waveforms

25. 25
References
• [1] “INTRODUCTIONto ADAPTIVE SIGNAL PROCESSING” Marc
Moonen ,Department of Electrical Engineering · ESAT/SISTA
K.U. Leuven, Leuven, Belgium
• [2] “Overview of Adaptive Filters”, Güner Arslan, from “Adaptive
Filter Theory”, 4e by Simon Haykin, ©2002 Prentice Hall Inc
• [3] Li Tan , Jean Jiang “Novel Adaptive IIR Filter for Frequency
Estimation and Tracking” , IEEE SIGNAL PROCESSING MAGAZINE
[186] NOVEMBER 2009