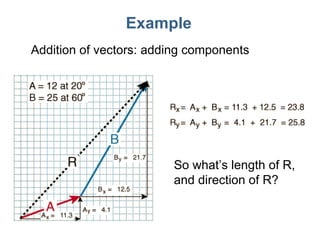
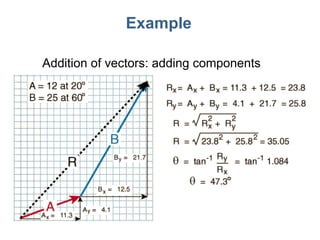
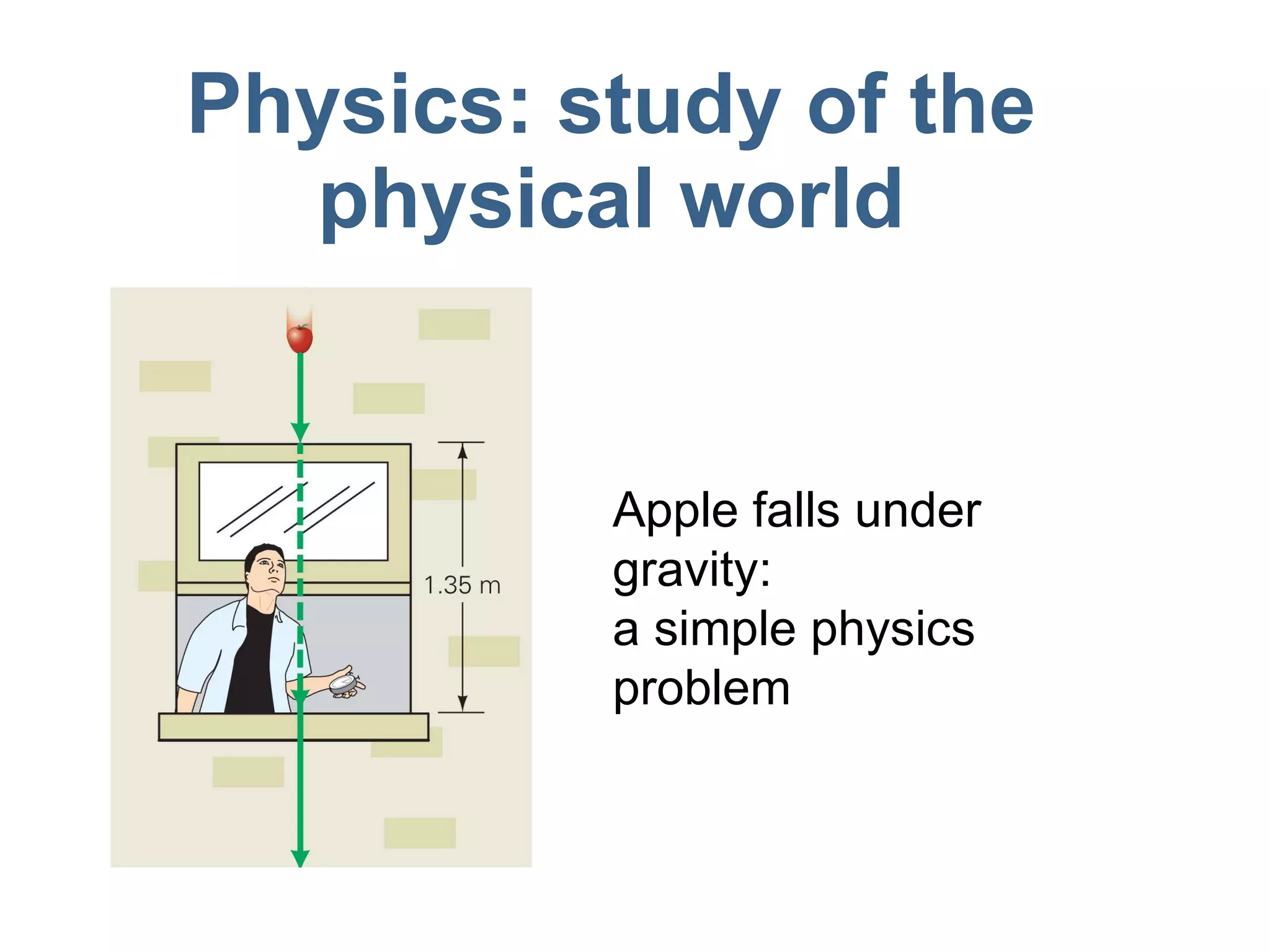
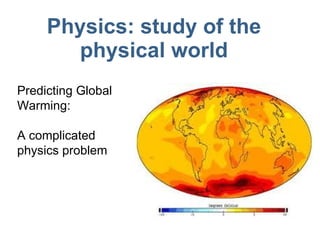
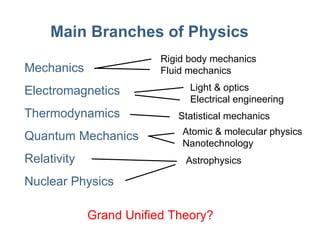
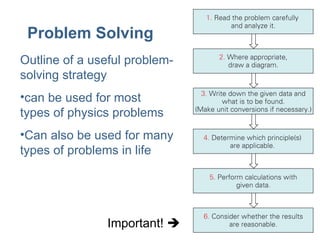
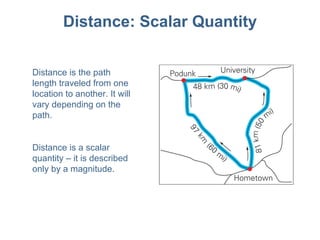
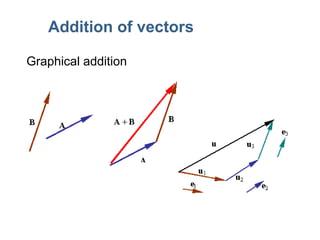
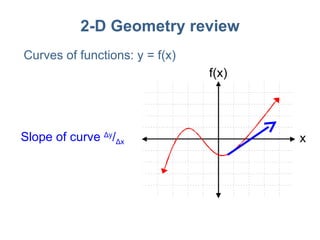
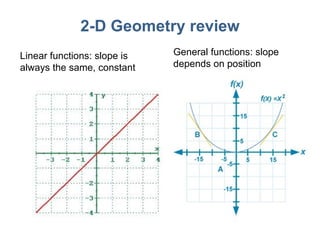
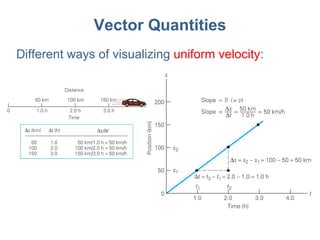
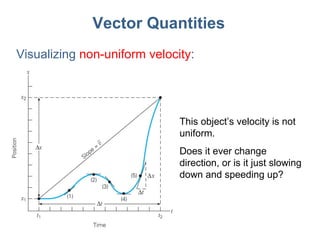
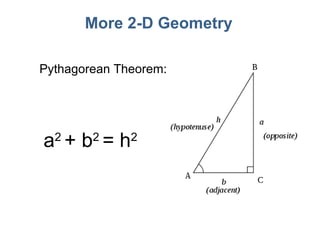
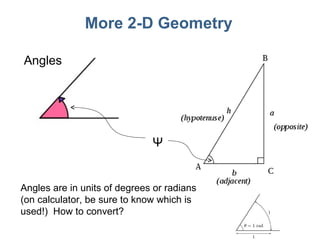
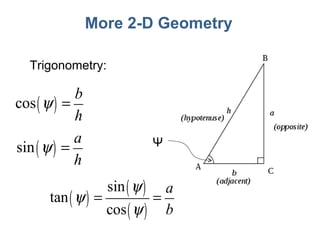
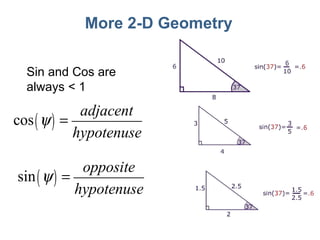
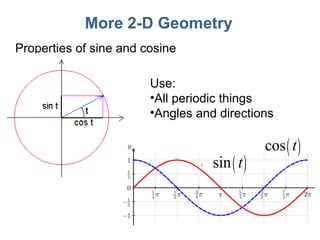
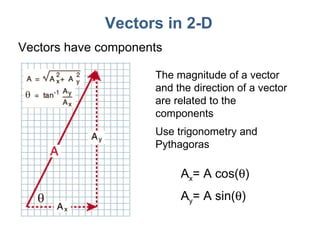
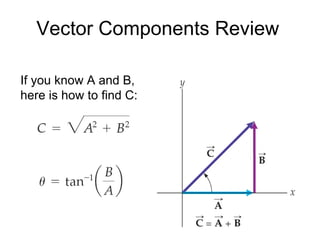
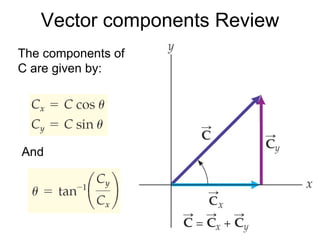
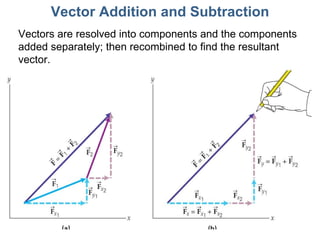
The document provides an overview of various topics in physics, including: 1) Examples of physics problems at different scales, from simple to complex. 2) The main branches of physics such as mechanics, electromagnetism, and quantum mechanics. 3) Mathematical concepts important for physics like scalars, vectors, geometry, trigonometry, and algebraic equations.

1. Physics: study of the physical world Apple falls under gravity: a simple physics problem

2. Physics: study of the physical world Rock climbing: a physics problem gravity friction energy Force

3. Physics: study of the physical world Predicting Global Warming: A complicated physics problem

4. Physics: study of the physical world Nano-technology: physicists do it

5. Physics: study of the physical world Origin of the universe: a physics problem

6. Main Branches of Physics Mechanics Electromagnetics Thermodynamics Quantum Mechanics Relativity Nuclear Physics Grand Unified Theory? Rigid body mechanics Fluid mechanics Light & optics Electrical engineering Atomic & molecular physics Nanotechnology Astrophysics Statistical mechanics

7. Problem Solving Outline of a useful problem-solving strategy can be used for most types of physics problems Can also be used for many types of problems in life Important! 

8. Math Basics Scalars & Vectors Dimensions & Units Geometry & Trigonometry f(x) A ϑ

9. Scalars and Vectors Scalar: magnitude only e.g.: 30 cookies Vector: magnitude and direction e.g.: 45 Newtons of force, upwards In physics, various quantities are either scalars or vectors.

10. Distance: Scalar Quantity Distance is the path length traveled from one location to another. It will vary depending on the path. Distance is a scalar quantity – it is described only by a magnitude.

11. Speed: Scalar Quantity Speed is distance ÷ time Since distance is a scalar, speed is also a scalar (and so is time) Instantaneous speed is the speed measured over a very short time span. This is what a speedometer in a car reads. Average speed is distance ÷ some larger time interval

12. Distance and Speed: Scalar Quantities Average speed is the distance traveled divided by the elapsed time: A bar over something usually denotes the average, also sometimes used: < S > A Δ (Greek: delta) is usually used to indicate a difference or interval (Δt = t 2 -t 1 )

13. Displacement: a Vector Displacement is a vector that points from the initial position to the final position of an object.

14. Vectors & dimensions A vector has both magnitude and direction In one dimension, a vector has one component. In two dimensions, a vector has two components. In three dimensions, vectors have three components… A vector is usually drawn as an arrow. It is often symbolized with a small arrow over (or sometimes under) a symbol: A

15. Addition of vectors Graphical addition

16. Vector Quantities: Velocity Note that an object ’s position coordinate may be negative, while its velocity may be positive – the two are independent. Velocity is a vector that points in the direction that an object is moving in

17. 2-D Geometry review Curves of functions: y = f(x) f(x) x Slope of curve Δy / Δx

18. 2-D Geometry review Linear functions: slope is always the same, constant General functions: slope depends on position

19. Vector Quantities Different ways of visualizing uniform velocity :

20. Vector Quantities This object ’s velocity is not uniform. Does it ever change direction, or is it just slowing down and speeding up? Visualizing non-uniform velocity :

21. More 2-D Geometry Pythagorean Theorem: a 2 + b 2 = h 2

22. More 2-D Geometry Angles are in units of degrees or radians (on calculator, be sure to know which is used!) How to convert? Ψ Angles

23. More 2-D Geometry Ψ Trigonometry:

24. More 2-D Geometry Sin and Cos are always < 1

25. More 2-D Geometry Properties of sine and cosine Use: All periodic things Angles and directions

26. One last mathematical tidbit Quadratic Formula: memorize it If faced with an equation where the unknown variable is squared, re-arrange things to look like this: Then x is given by: (There are two possible solutions)

27. Vectors in 2-D Vectors have components The magnitude of a vector and the direction of a vector are related to the components Use trigonometry and Pythagoras A x = A cos(  ) A y = A sin(  )

28. Manipulating Vectors in 2-D Adding things in one dimension is easy: 3 Apples + 2 Apples = 5 Apples But in two (or more) dimensions: we add the components: if we have a vector {x Apples, y Oranges} {2 Apples, 3 Oranges} + {5 Apples, 2 Oranges} = (2+5) Apples, (3+2) Oranges = 7 Apples, 5 Oranges

29. Vector Components Review If you know A and B, here is how to find C:

30. Vector components Review The components of C are given by: And

31. Vector Addition and Subtraction Vectors are resolved into components and the components added separately; then recombined to find the resultant vector.

32. Example Addition of vectors: adding components So what’s length of R, and direction of R?

33. Example Addition of vectors: adding components