1) The document discusses dimensions and units in engineering dynamics, explaining that equations represent equality where the dimensions and units of both sides must match.
2) It covers dimensional analysis, defining common engineering quantities like force, pressure, work, and power in terms of mass, length, and time dimensions.
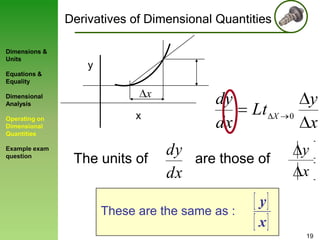
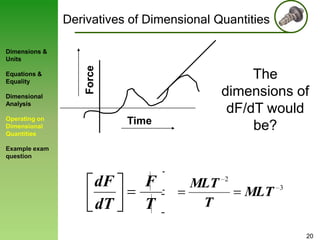
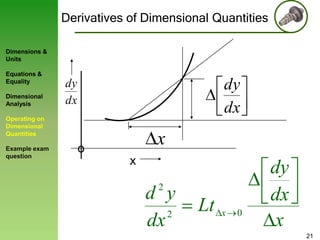
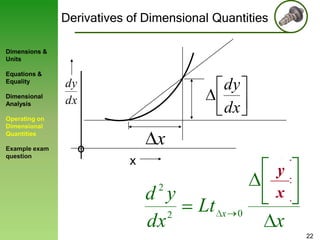
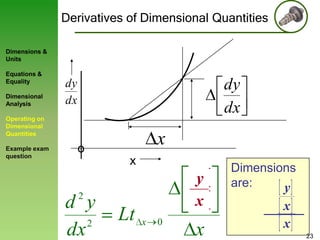
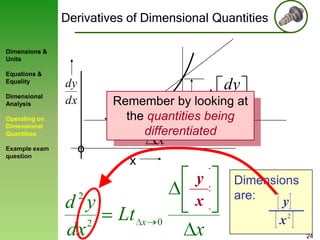
3) Rules for operating on dimensional quantities are presented, showing that derivatives and integrals retain the dimensions of the original terms.





![Equations & Equality
Dimensions &
Units
A familiar example:
Equations &
Equality
Dimensional
Analysis
Operating on
Dimensional
Quantities
Example exam
question
s ut
1 2
at
2
The dimensions of the LHS are
denoted:
LHS: [ s ] = length = L
6](https://image.slidesharecdn.com/eng1040lec02-131029001456-phpapp02/85/ENG1040-Lec02-6-320.jpg)


![Equations & Equality
Dimensions &
Units
Equations &
Equality
Dimensional
Analysis
Operating on
Dimensional
Quantities
A familiar example:
s ut
1 2
at
2
The dimensions of both sides are: length, [L]
Example exam
question
The equation is dimensionally homogeneous
9](https://image.slidesharecdn.com/eng1040lec02-131029001456-phpapp02/85/ENG1040-Lec02-9-320.jpg)


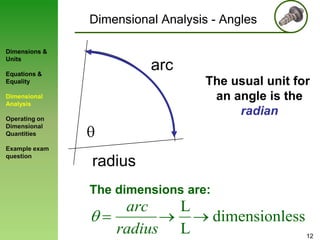
![Dimensional Analysis - Angles
Dimensions &
Units
Frequency, and angular speed may be
measured in units of…
Equations &
Equality
Dimensional
Analysis
Operating on
Dimensional
Quantities
Example exam
question
radian s-1 (rad/s)
revolutions s -1 (Hz)
revolutions min -1 (RPM)
We use the S.I. unit to find its dimensions,
i.e. rad/s [T]-1
13](https://image.slidesharecdn.com/eng1040lec02-131029001456-phpapp02/85/ENG1040-Lec02-13-320.jpg)

![Dimensional Analysis - Pressure
Dimensions &
Units
Pressure has units of Force per unit area:
Equations &
Equality
Dimensional
Analysis
Operating on
Dimensional
Quantities
Example exam
question
The dimensions are:
[P] = [Force/Area] = MLT-2/L2
= ML-1T-2
This unit is called a Pascal
15](https://image.slidesharecdn.com/eng1040lec02-131029001456-phpapp02/85/ENG1040-Lec02-15-320.jpg)
![Dimensional Analysis - Work
Dimensions &
Units
Equations &
Equality
Dimensional
Analysis
Operating on
Dimensional
Quantities
Example exam
question
Work has units of
Force times distance,
The dimensions are thus
[W] = [Force*Distance] = (M LT-2) L
= M L2 T-2
This unit is called a Joule – i.e. a Nm.
16](https://image.slidesharecdn.com/eng1040lec02-131029001456-phpapp02/85/ENG1040-Lec02-16-320.jpg)
![Dimensional Analysis - Power
Dimensions &
Units
Equations &
Equality
Dimensional
Analysis
Operating on
Dimensional
Quantities
Example exam
question
Power has units of:
Force times velocity.
The dimensions are thus
[P] = [Force*Velocity] = (M LT-2) (LT-1)
= M L2 T-3
This unit is called a Watt – i.e. Nm/s.
17](https://image.slidesharecdn.com/eng1040lec02-131029001456-phpapp02/85/ENG1040-Lec02-17-320.jpg)

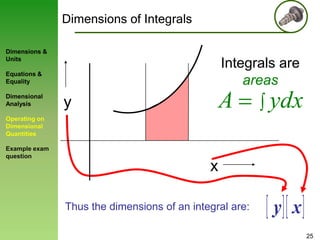
![Dimensions of Integrals
Dimensions &
Units
E.g., Impulse:
t2
Impulse
Equations &
Equality
Dimensional
Analysis
Fdt
t1
Force
Operating on
Dimensional
Quantities
Example exam
question
t1
Time
t2
ML
T
Units of Impulse = [F][t] =
T
2
= MLT-1
26](https://image.slidesharecdn.com/eng1040lec02-131029001456-phpapp02/85/ENG1040-Lec02-26-320.jpg)




![Conclusion
• To ensure an equation is dimensionally
homogeneous, ensure that the units are the
same (SI or Imperial) for every term on both LHS
and RHS
• All engineering dynamics equations can be
described by the 3 dimensions, mass [M], time
[T] and length [L].
31](https://image.slidesharecdn.com/eng1040lec02-131029001456-phpapp02/85/ENG1040-Lec02-31-320.jpg)