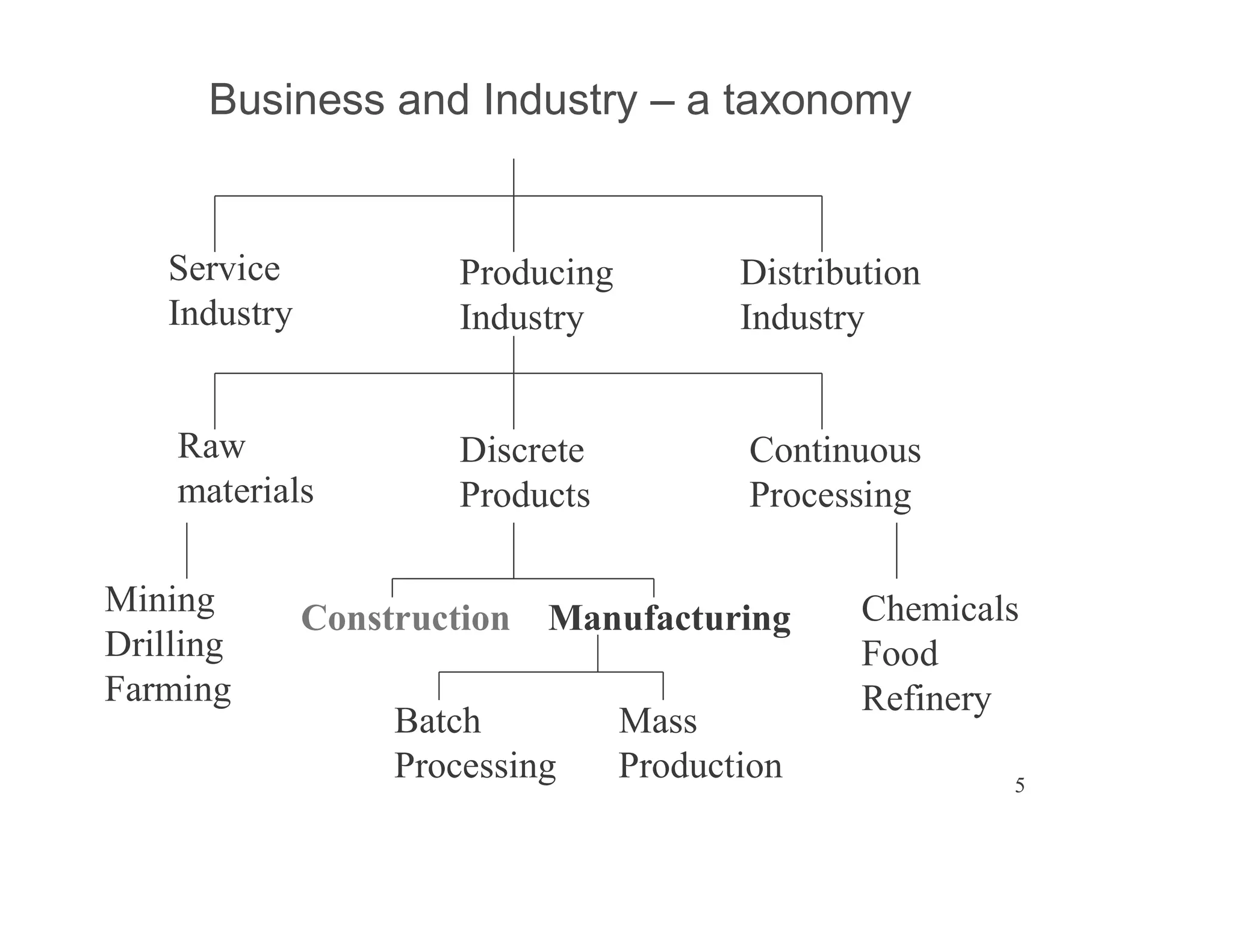
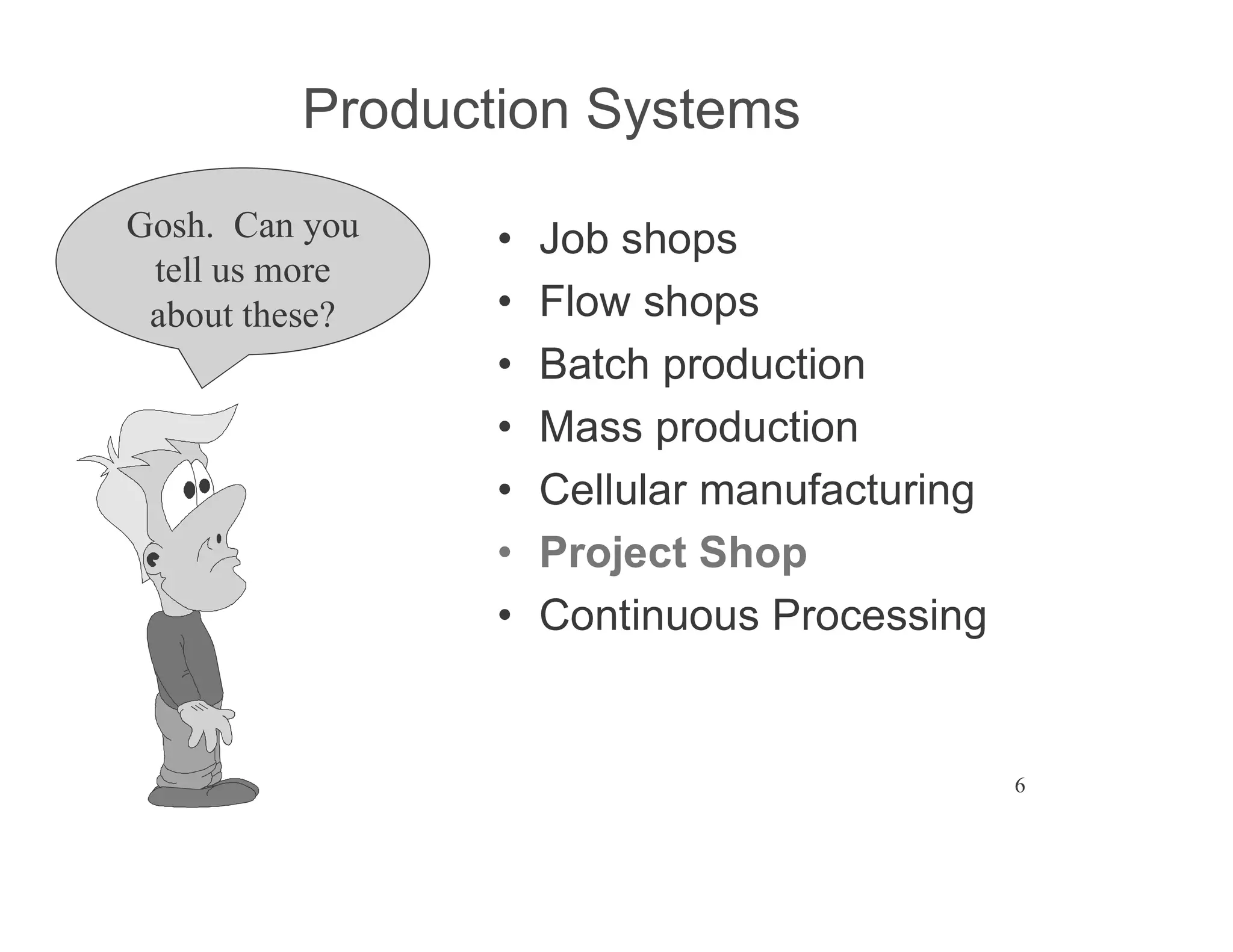
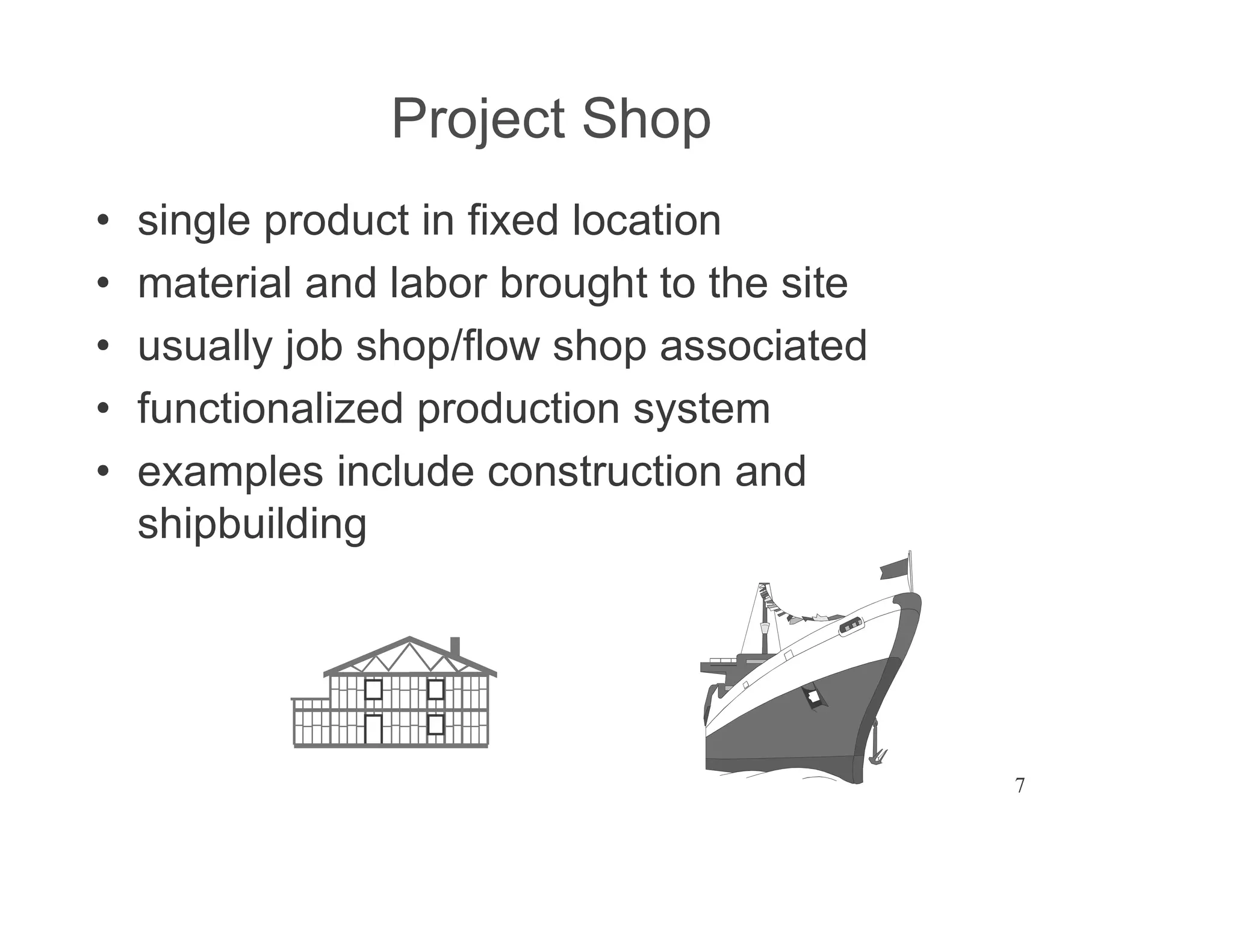
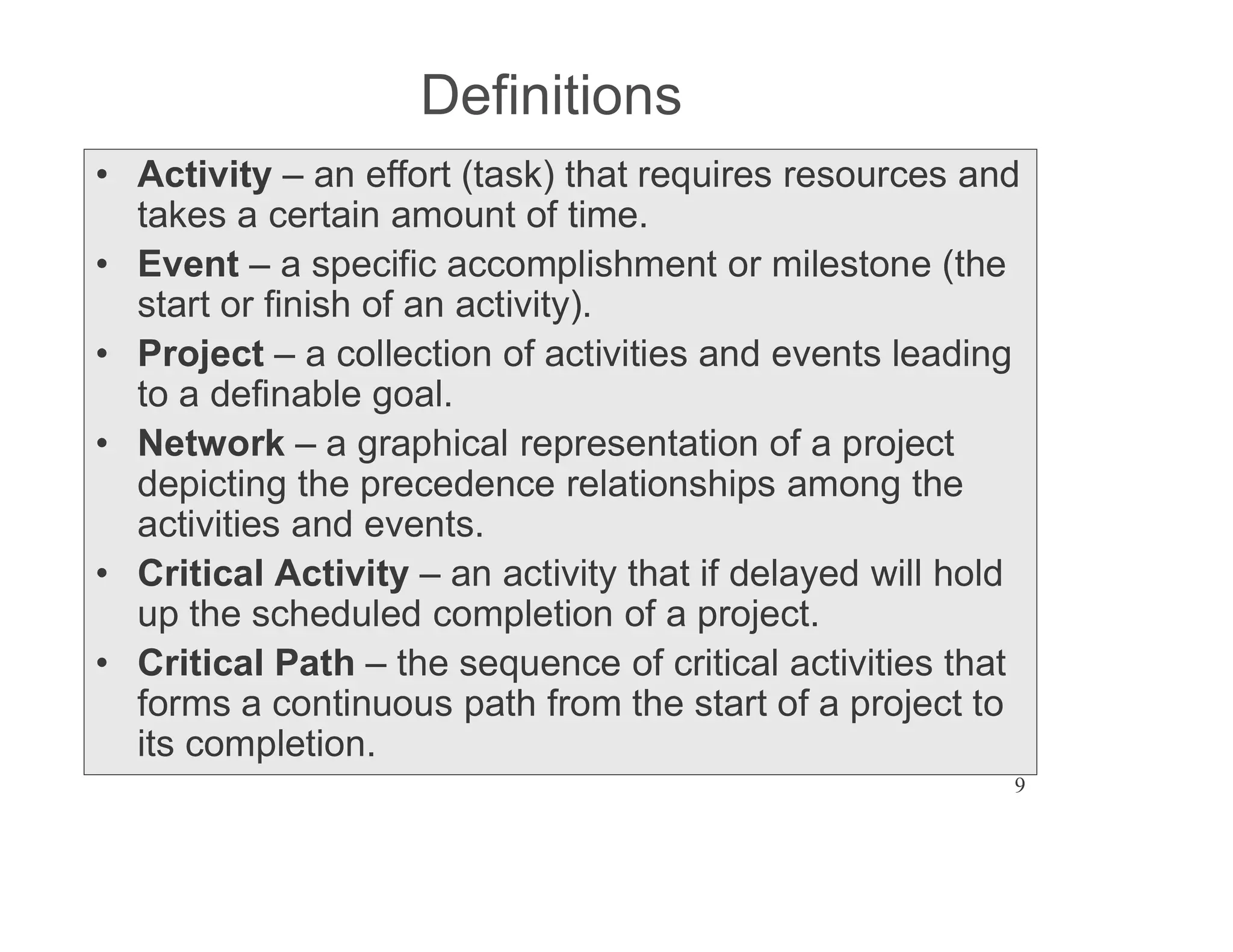
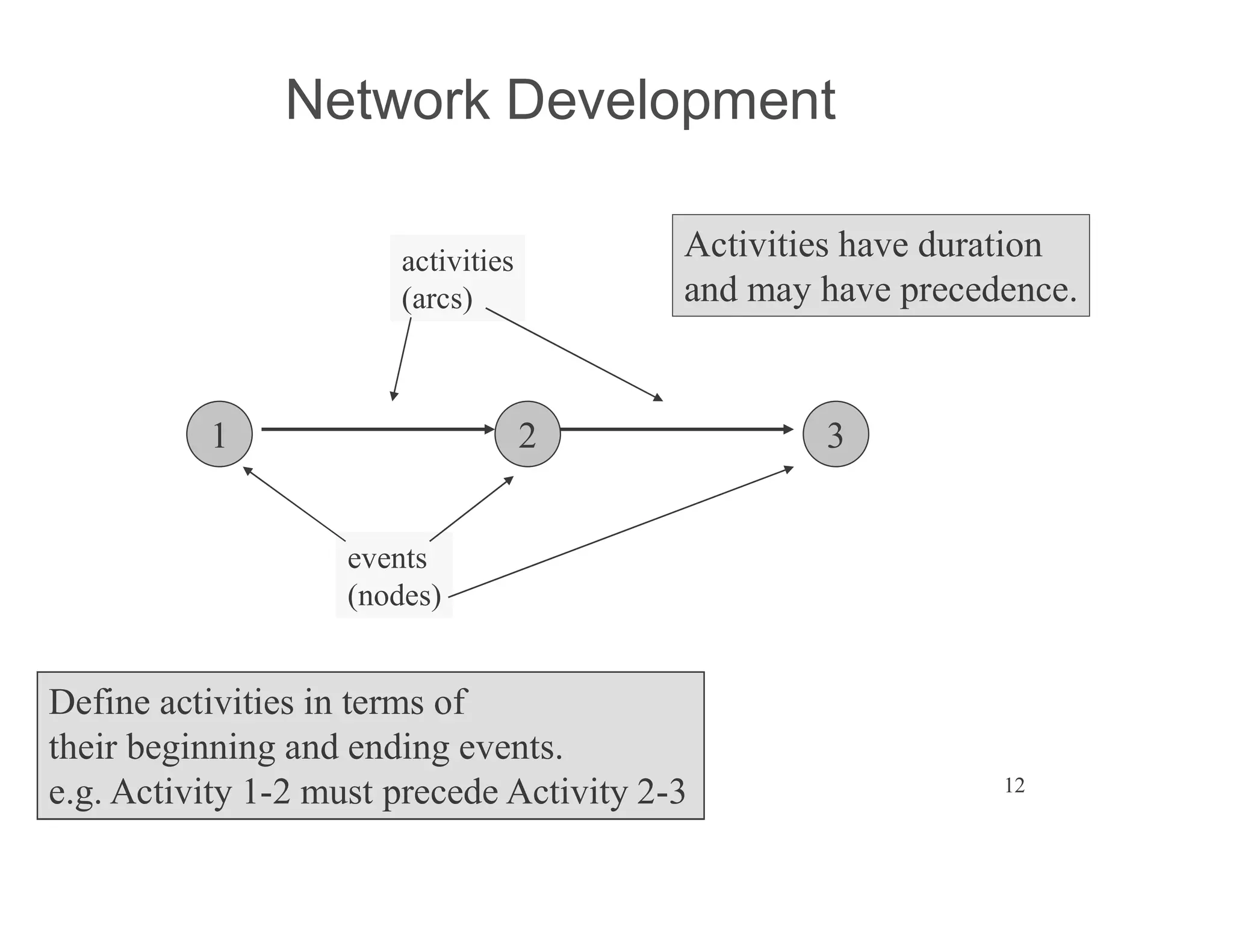
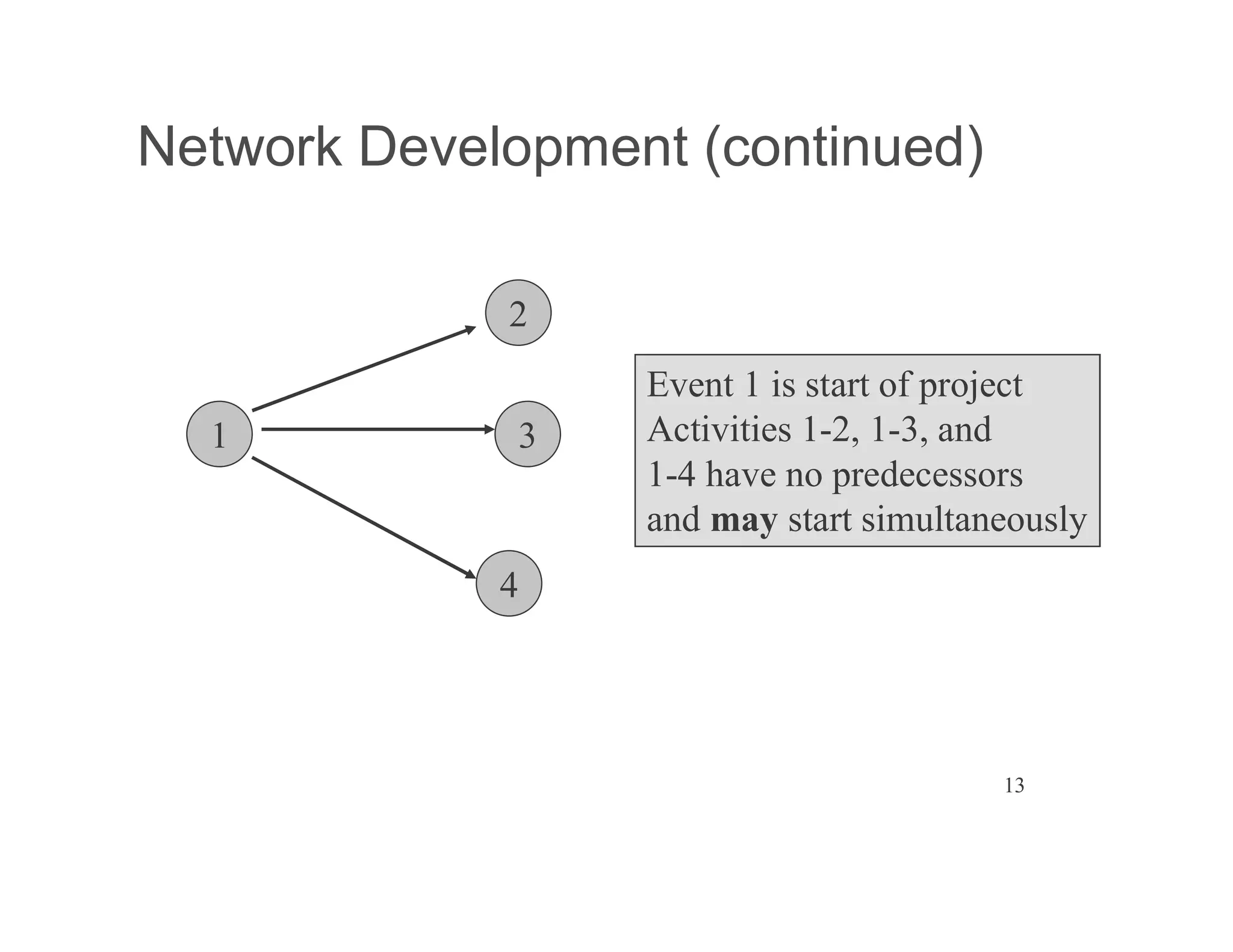
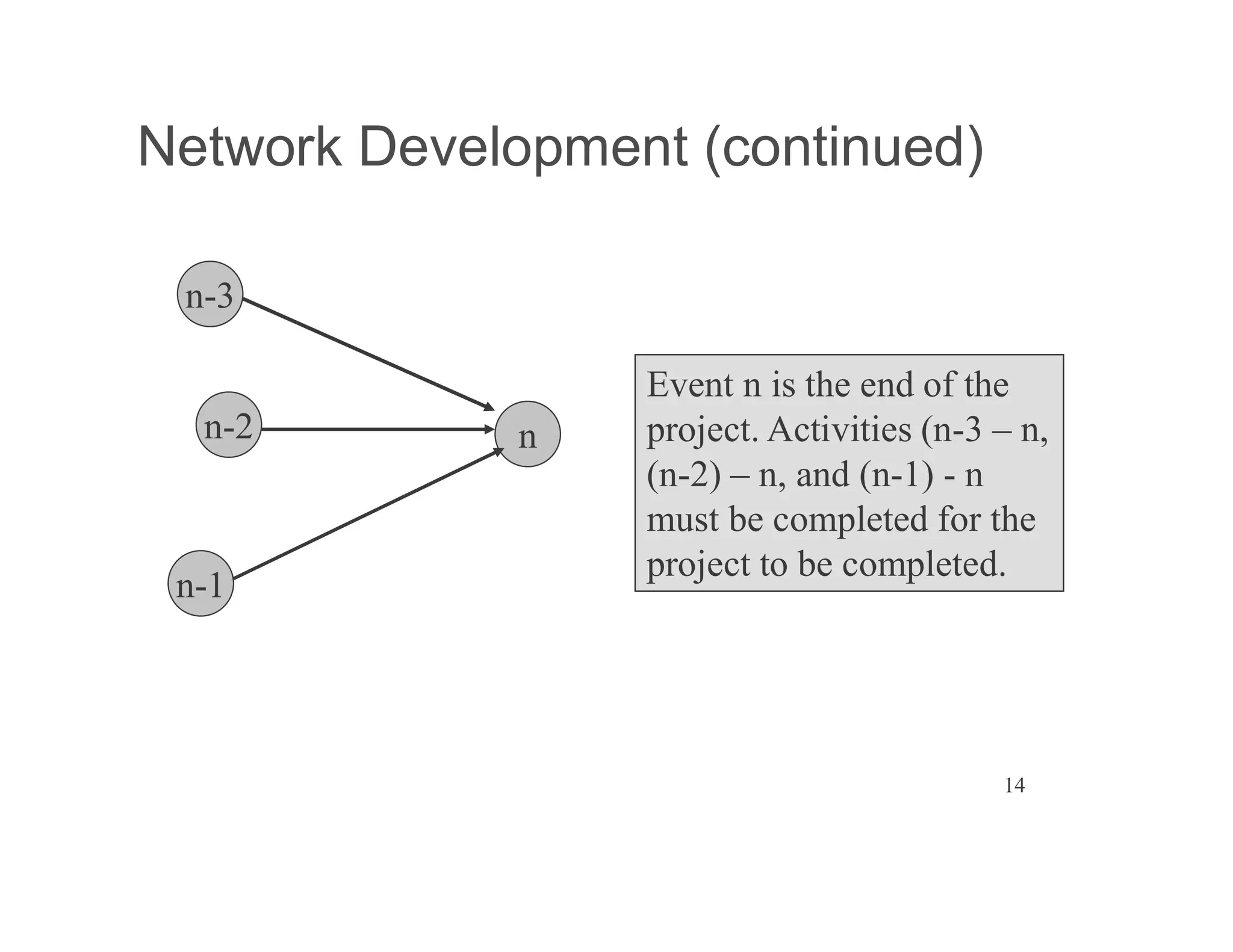
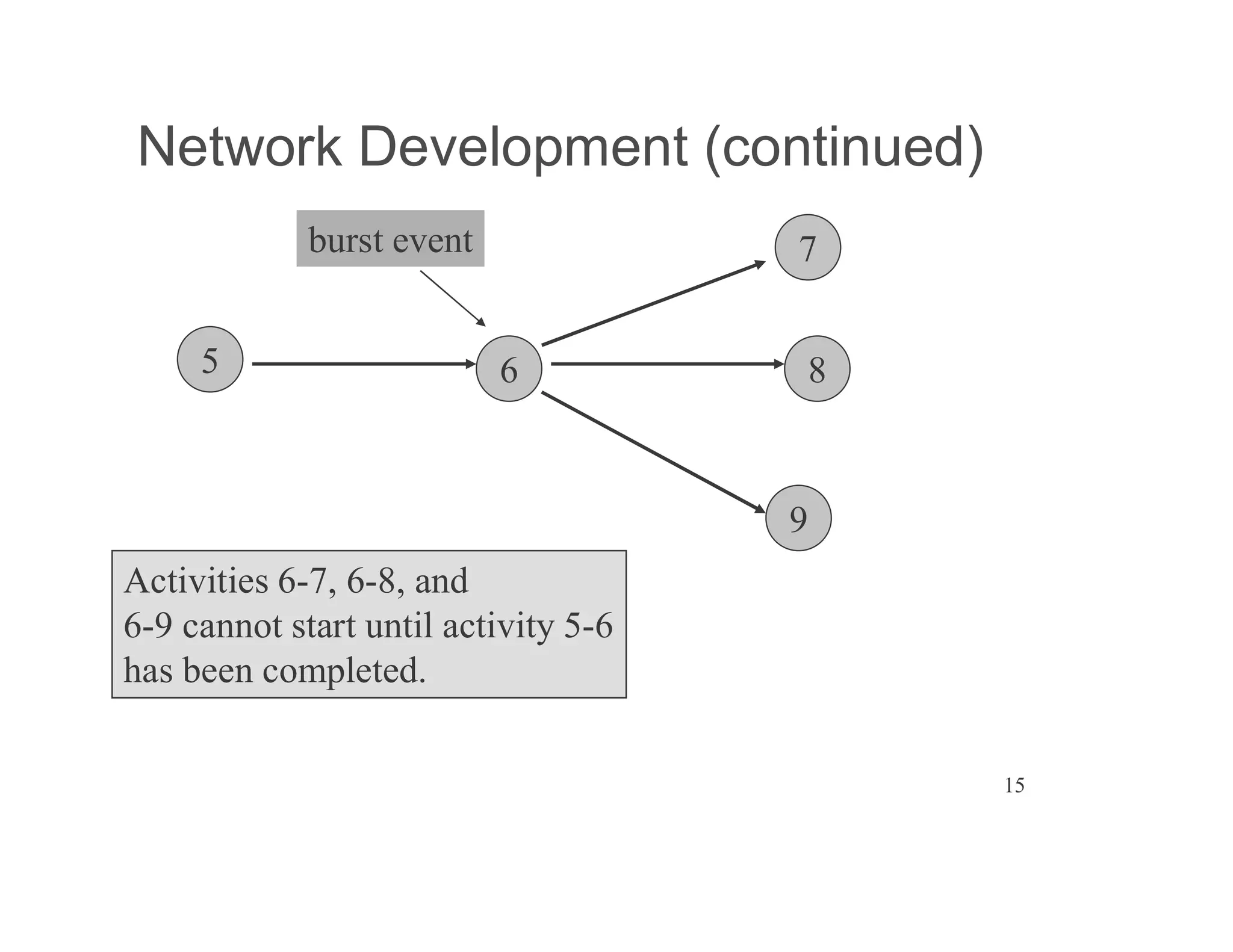
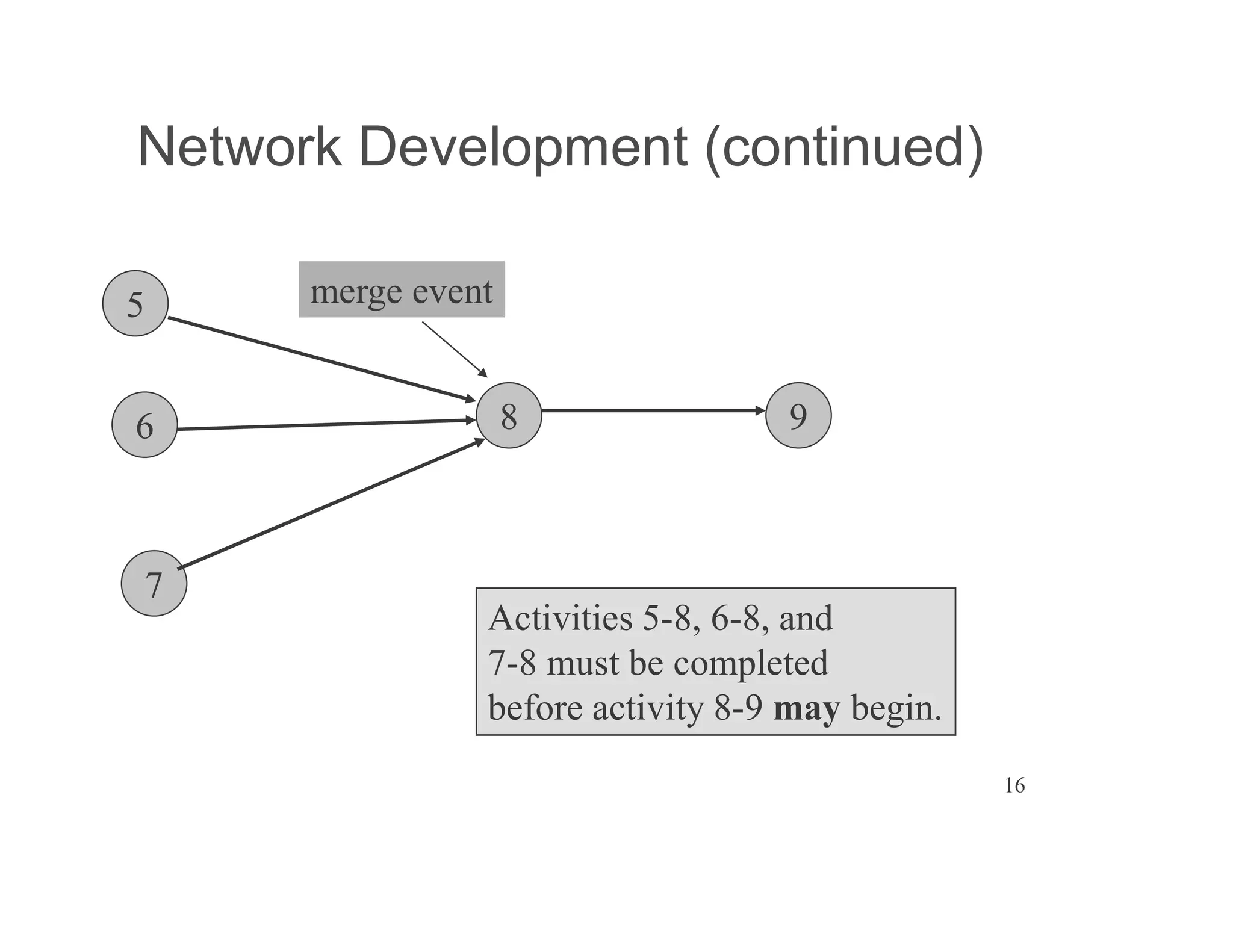
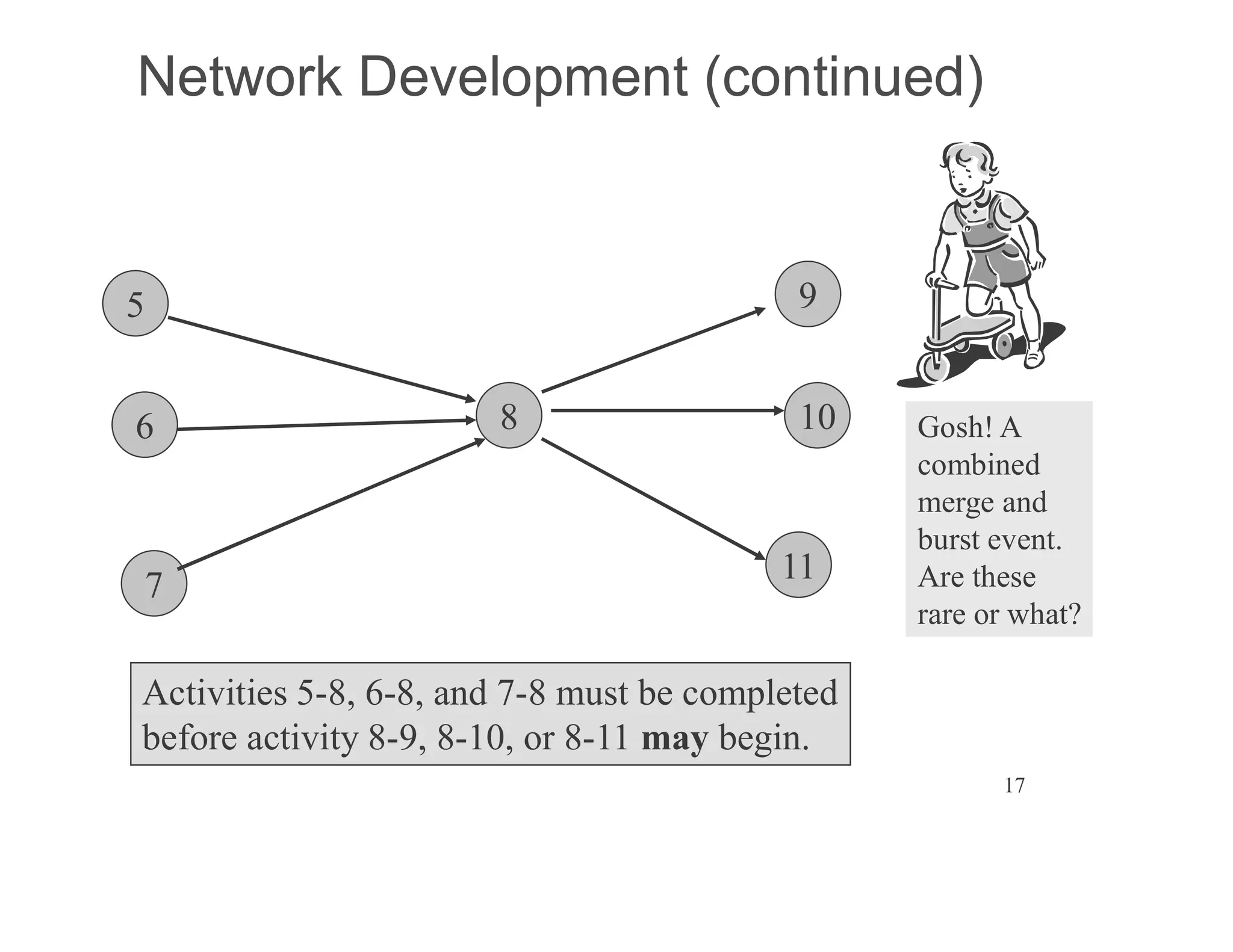
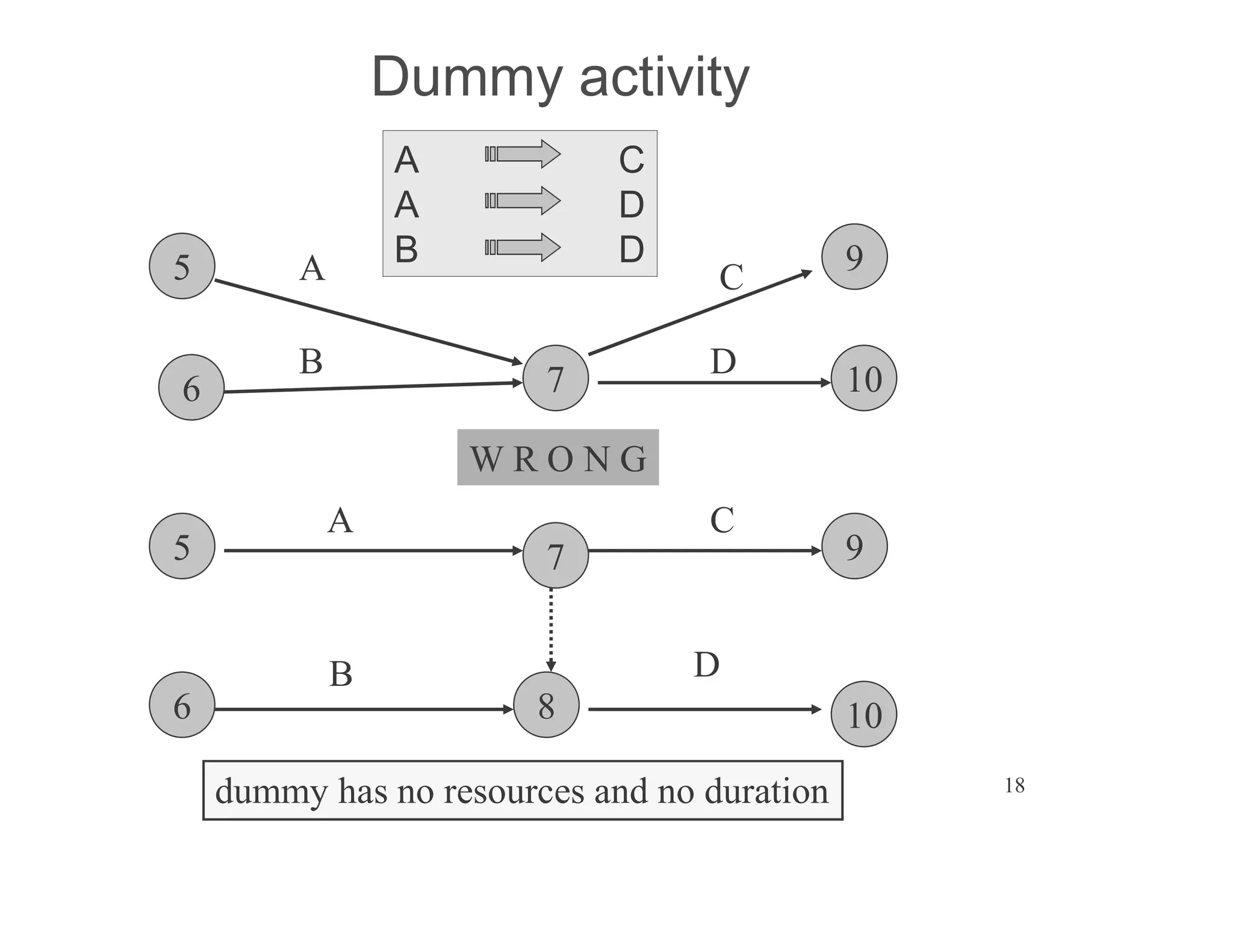
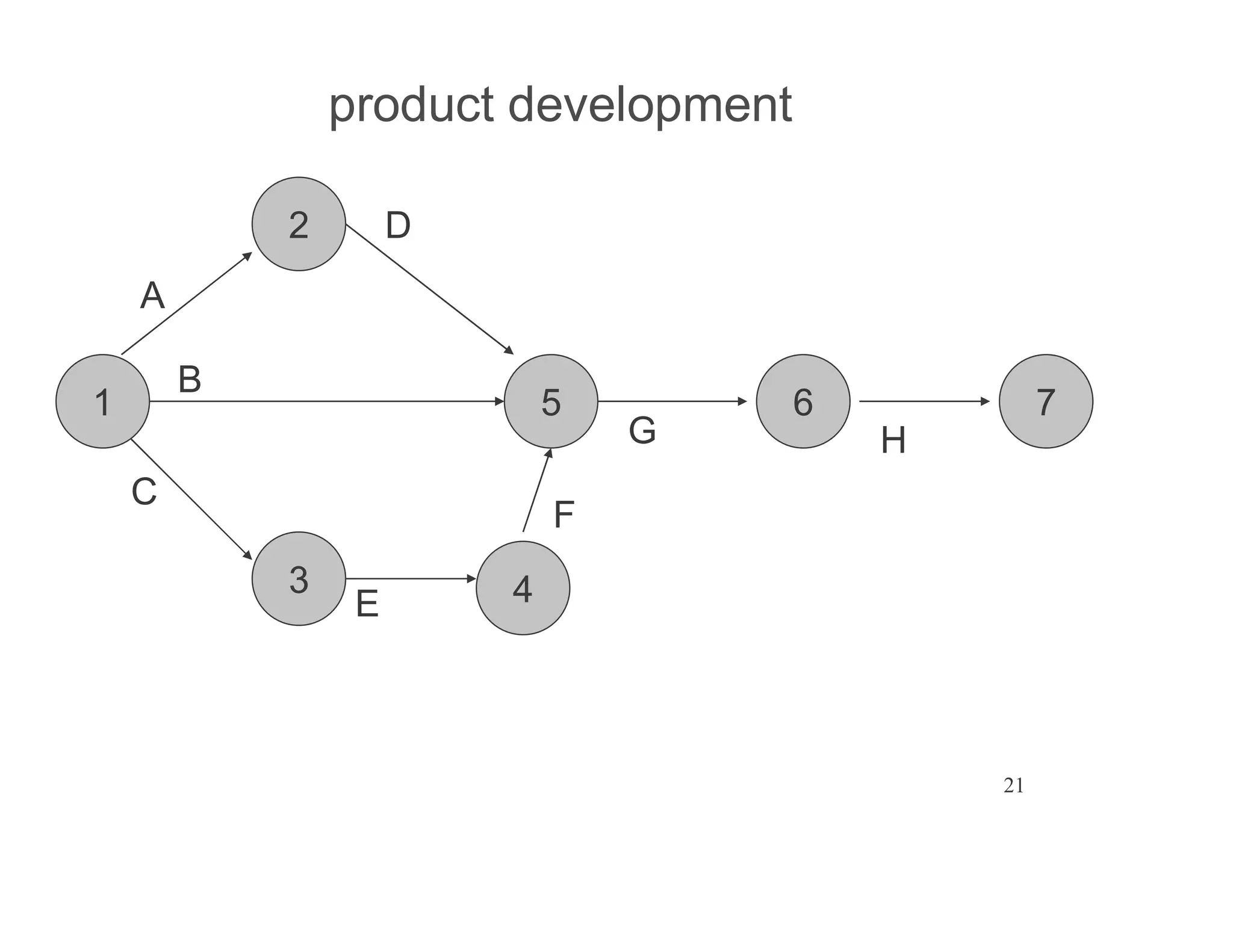
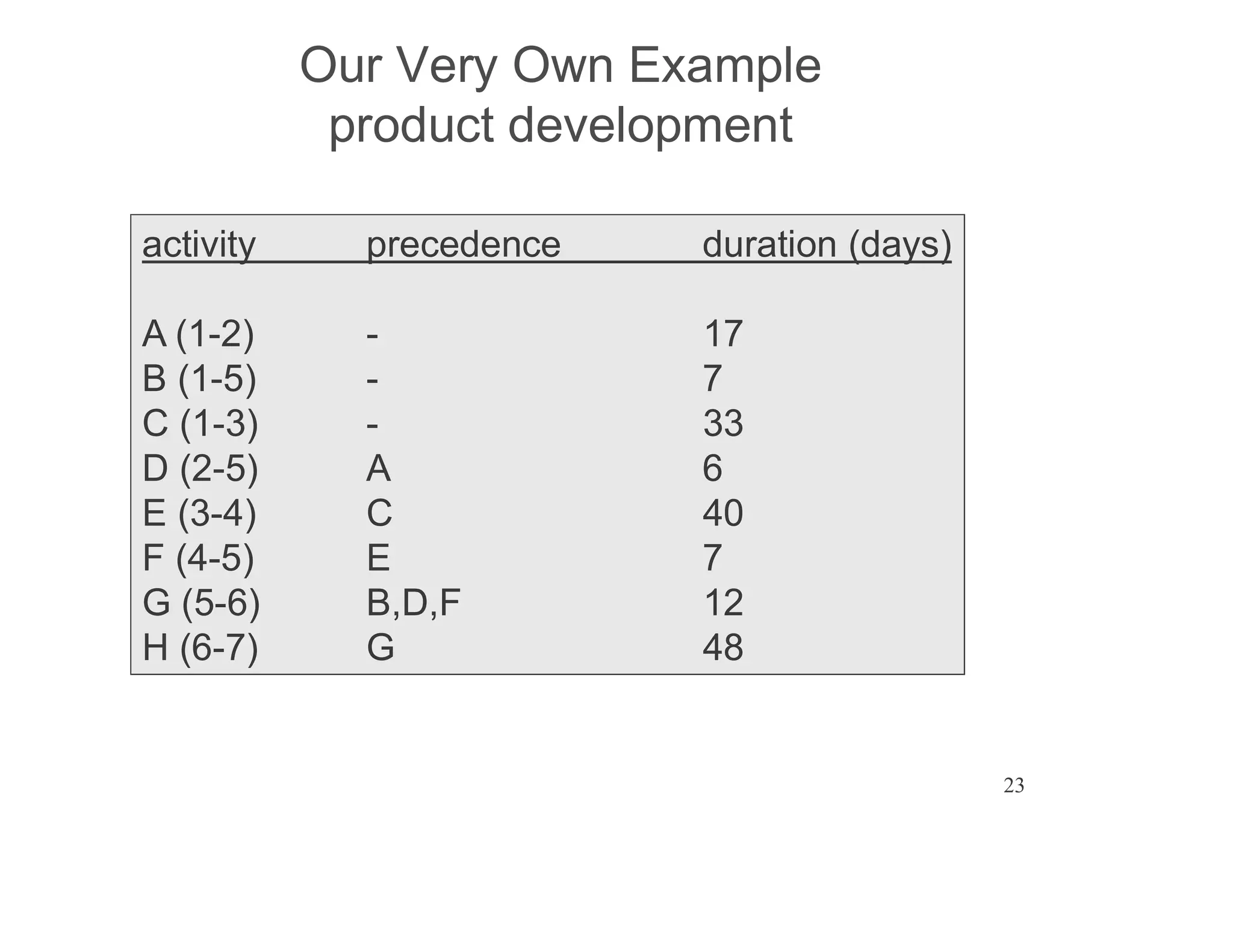
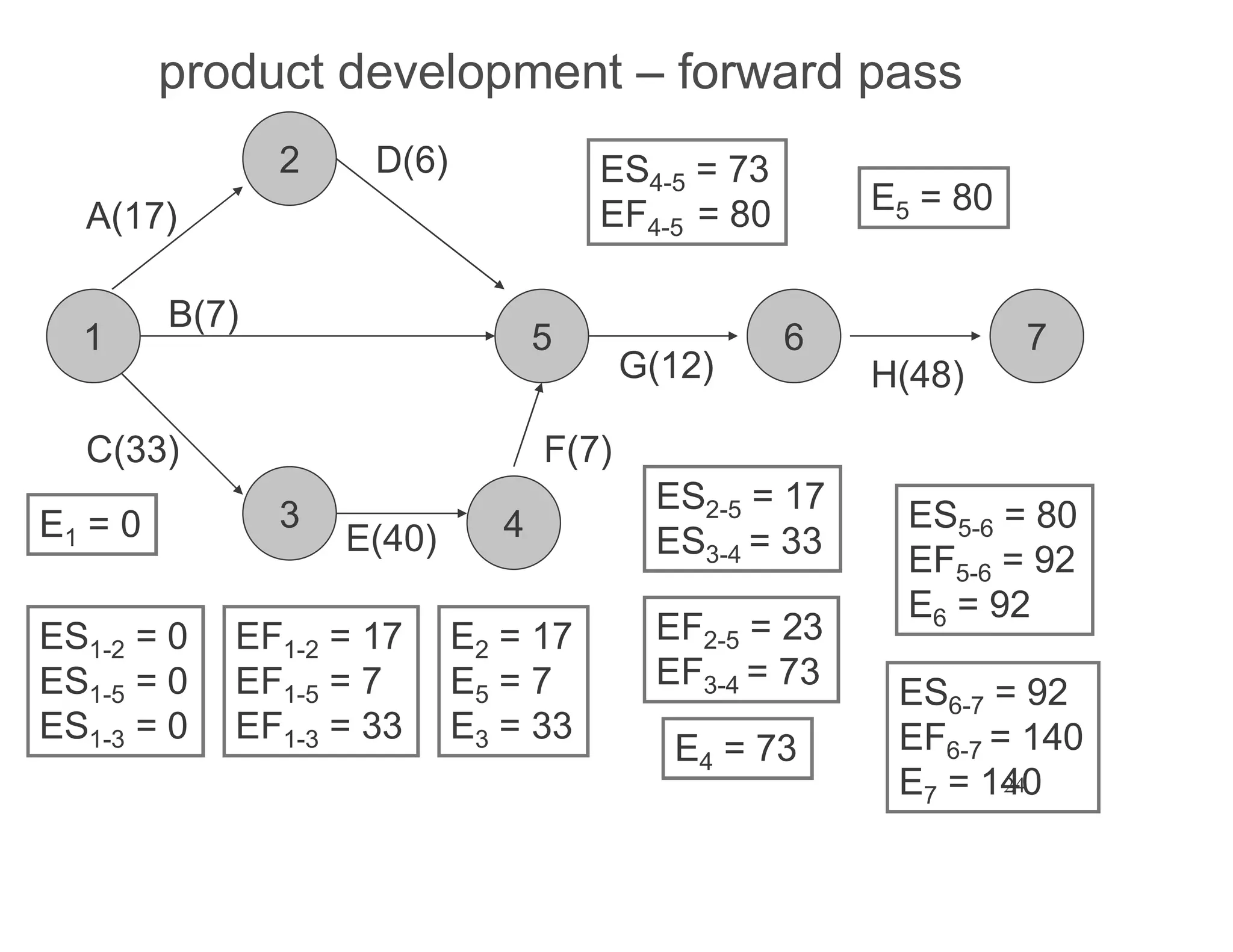
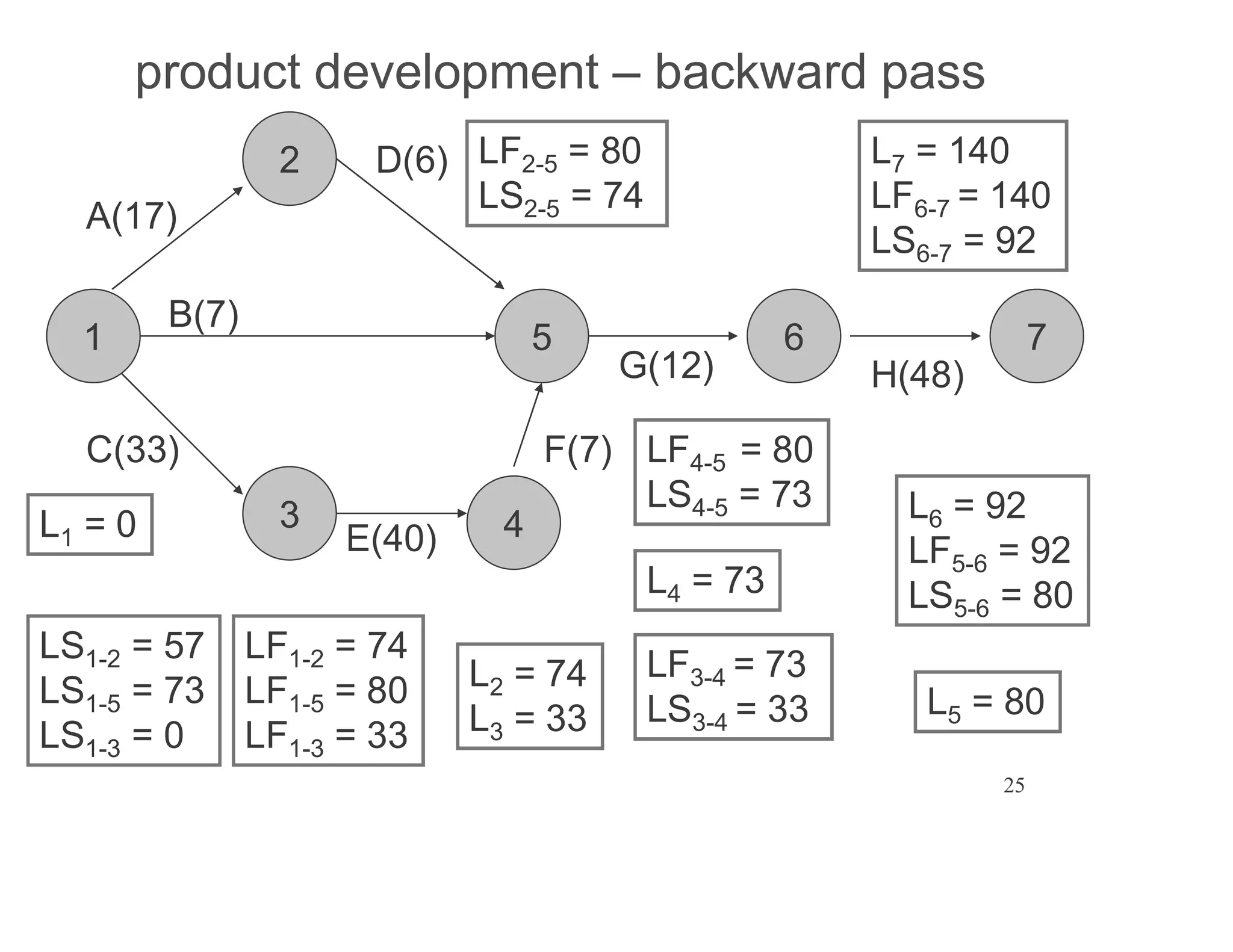
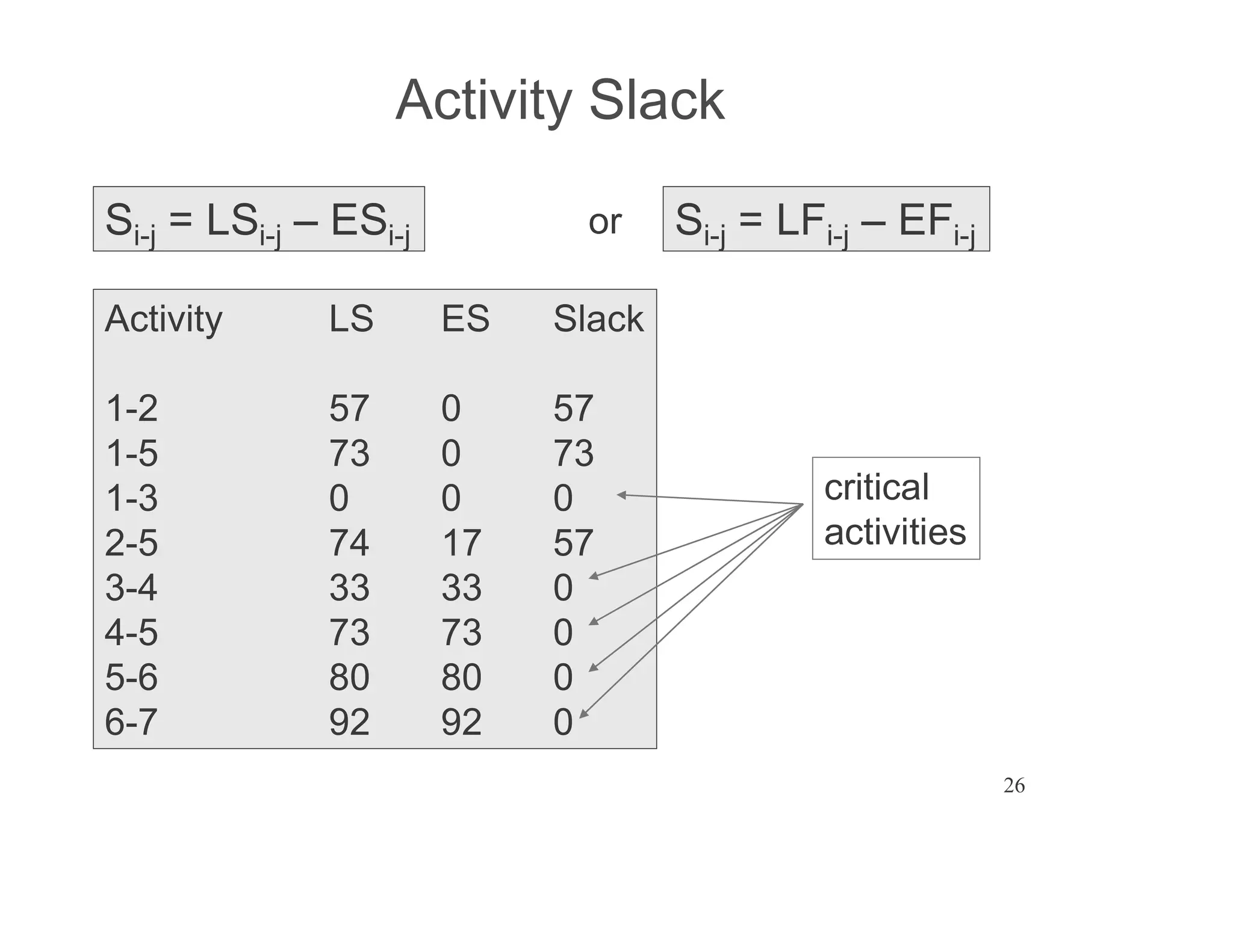
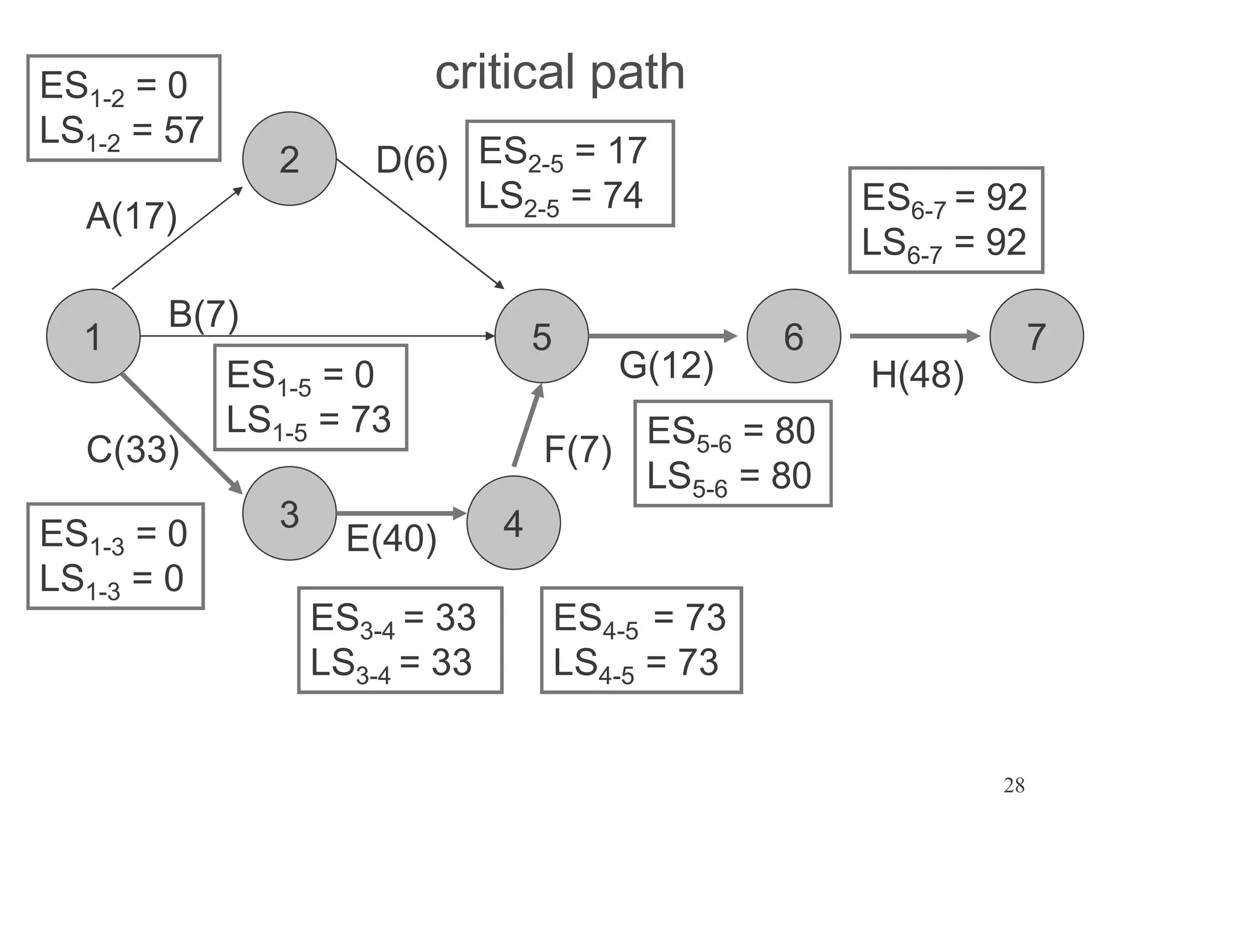
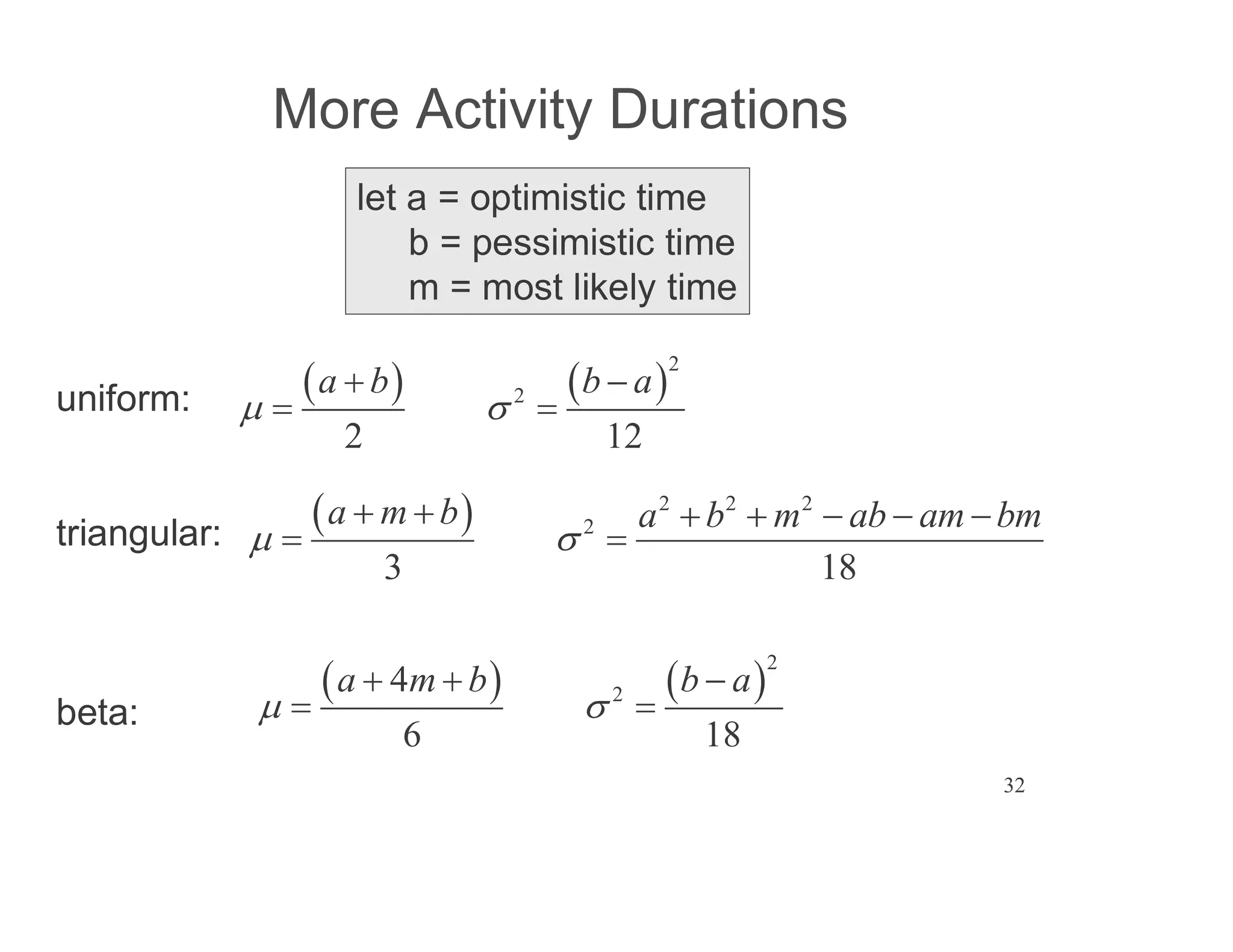
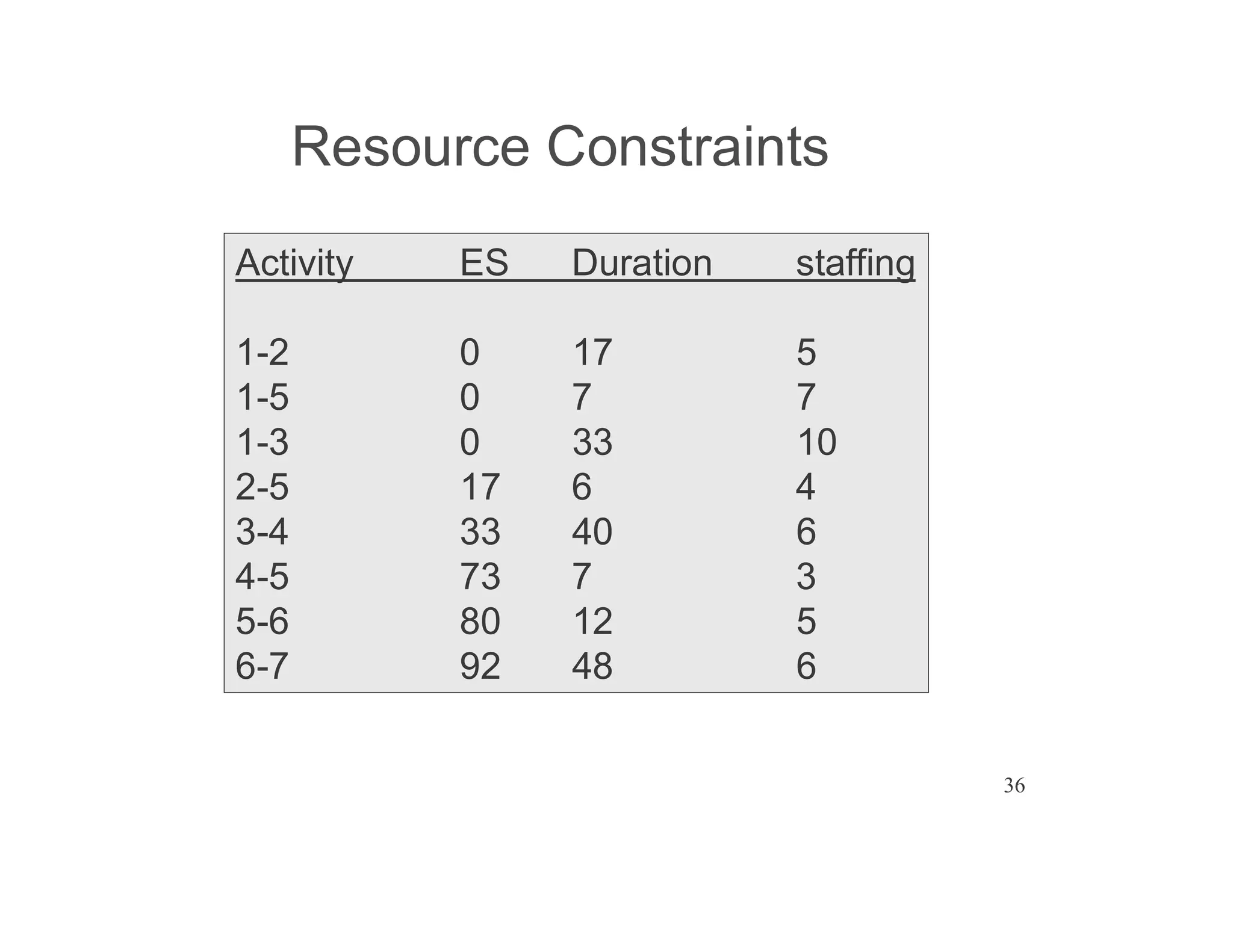
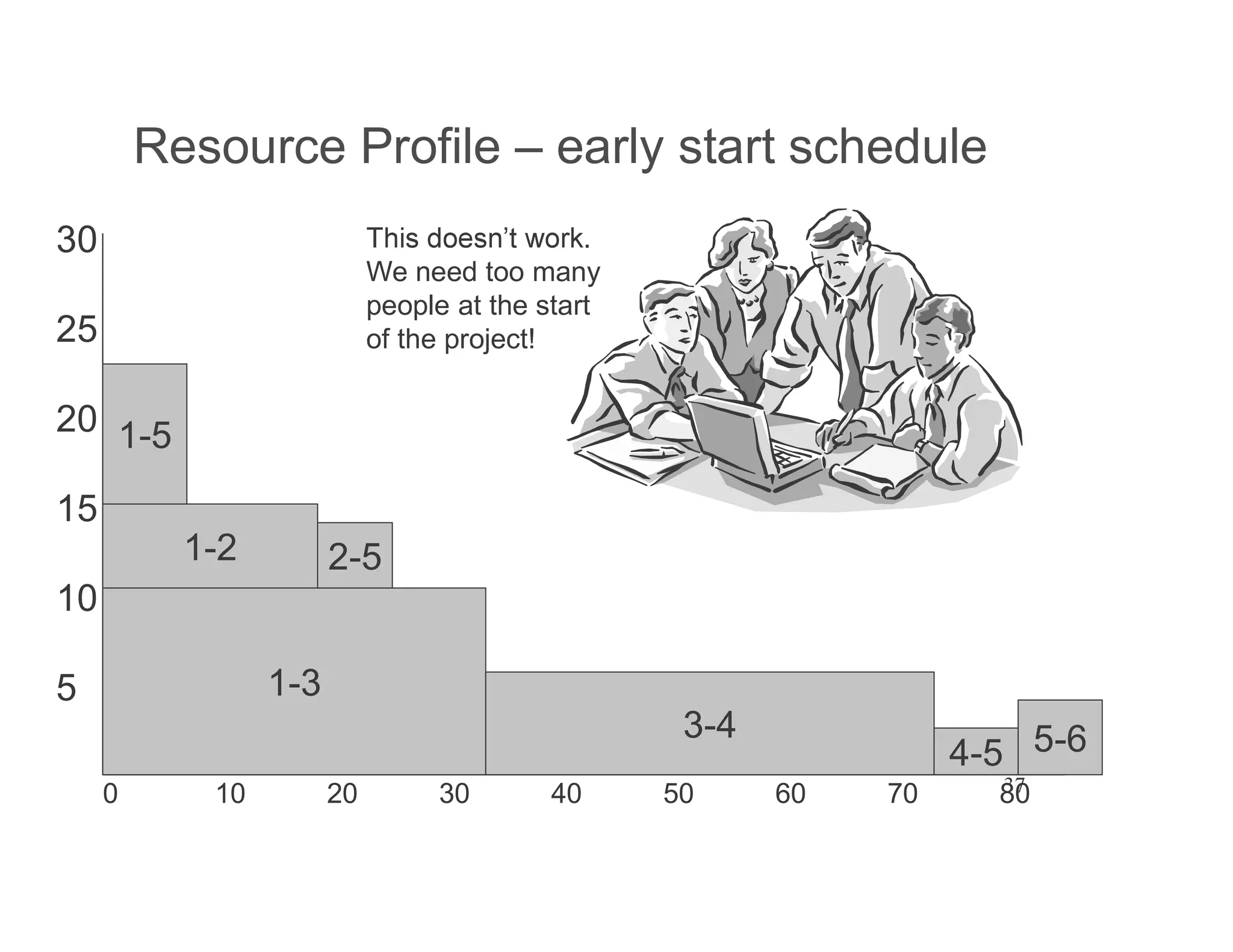
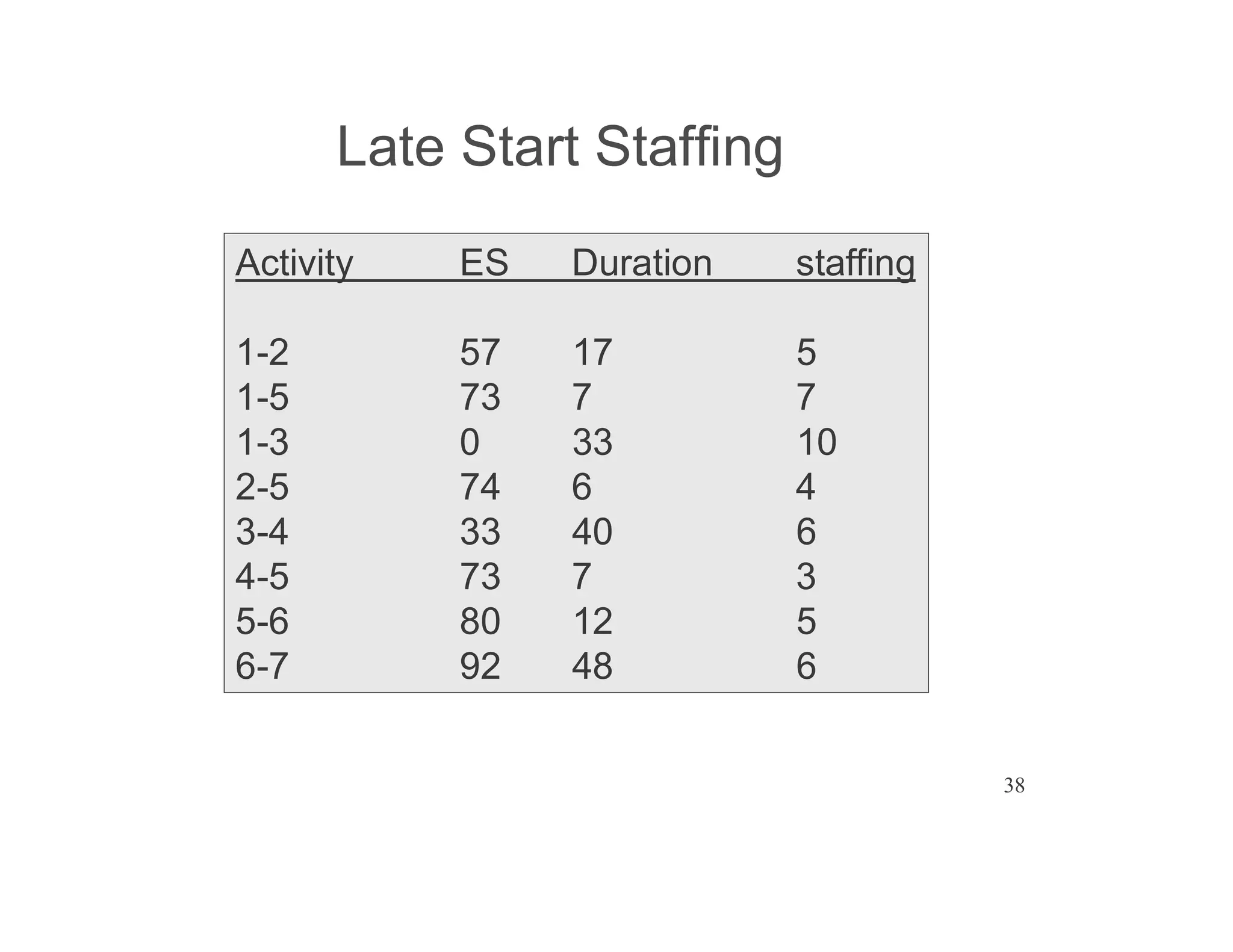
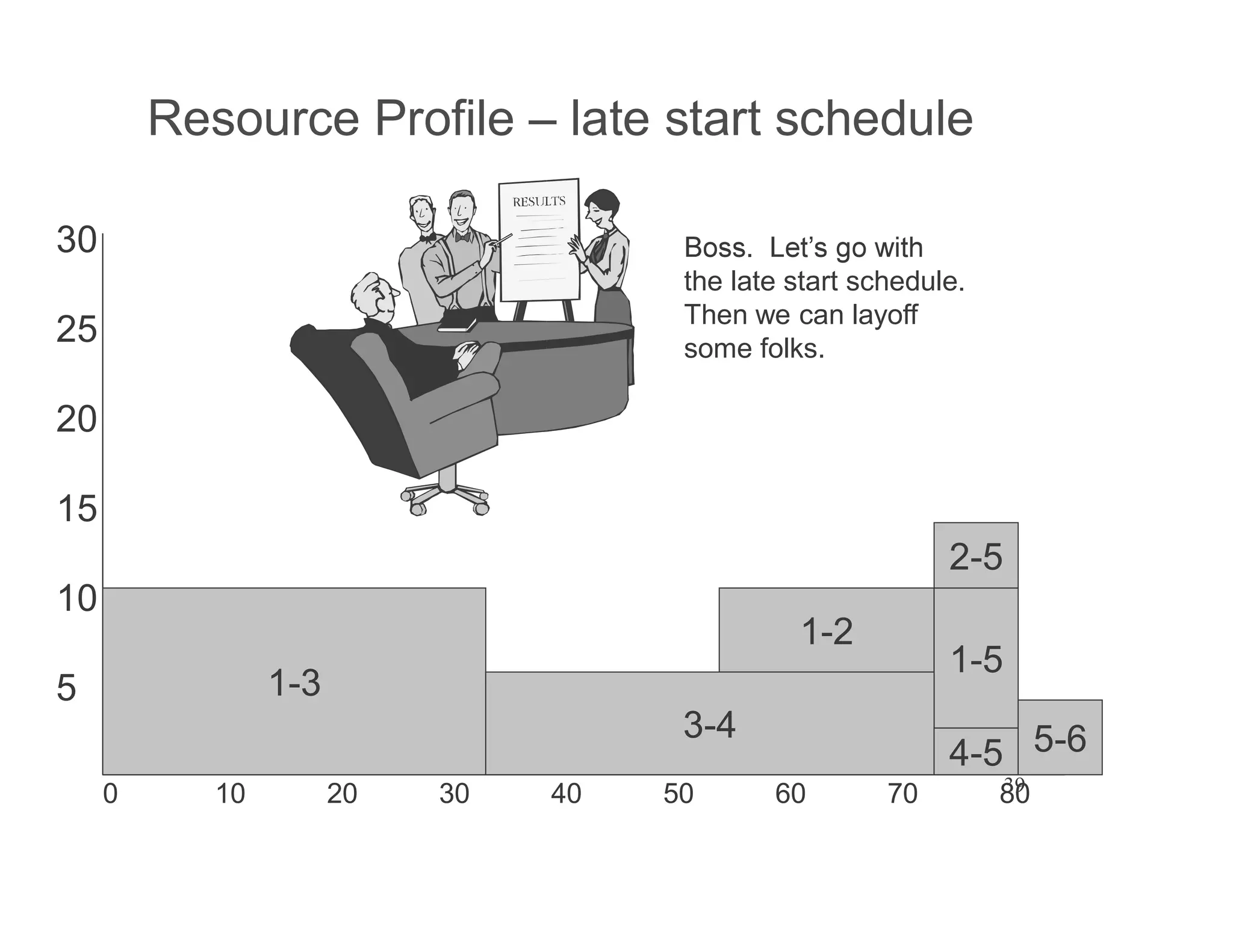
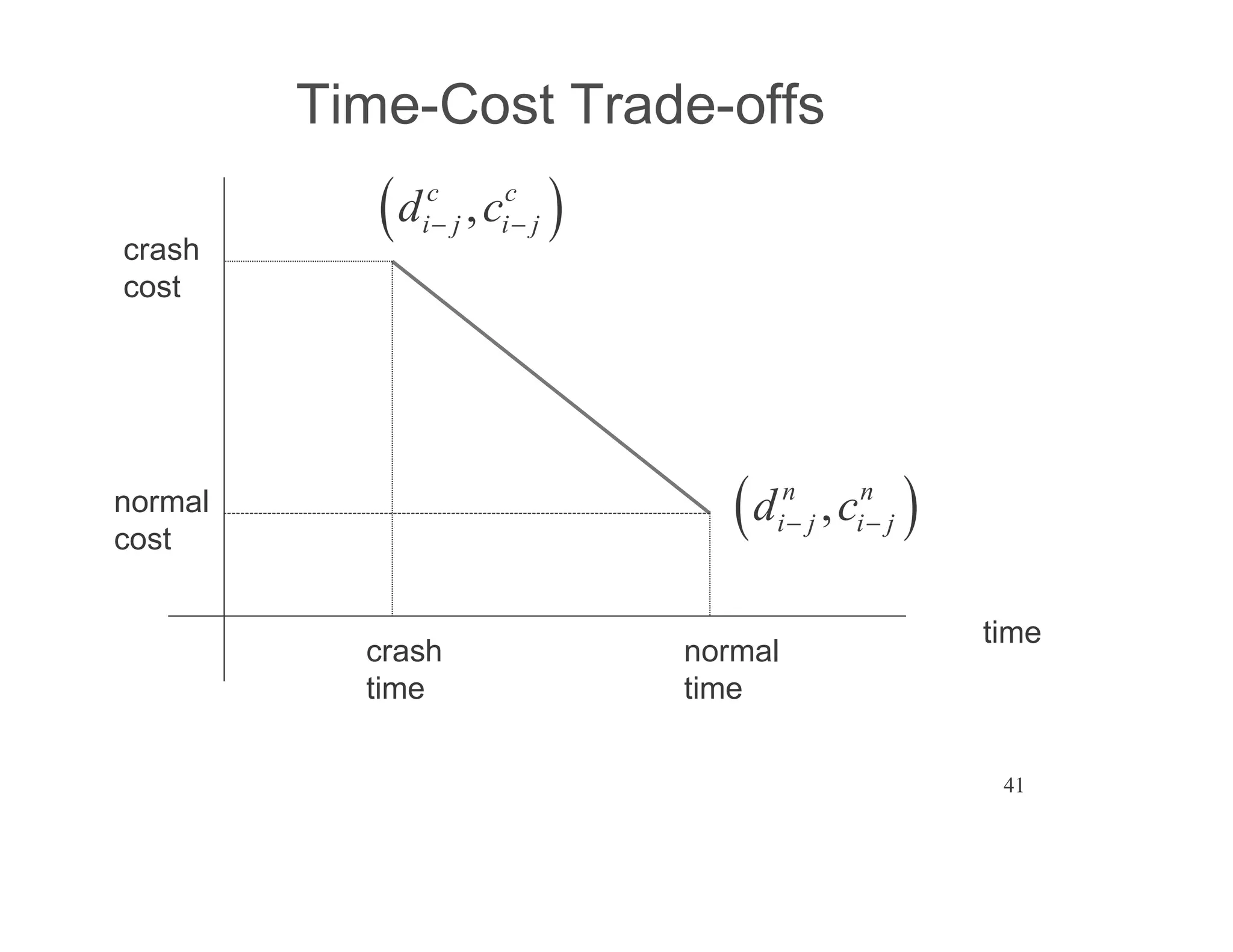
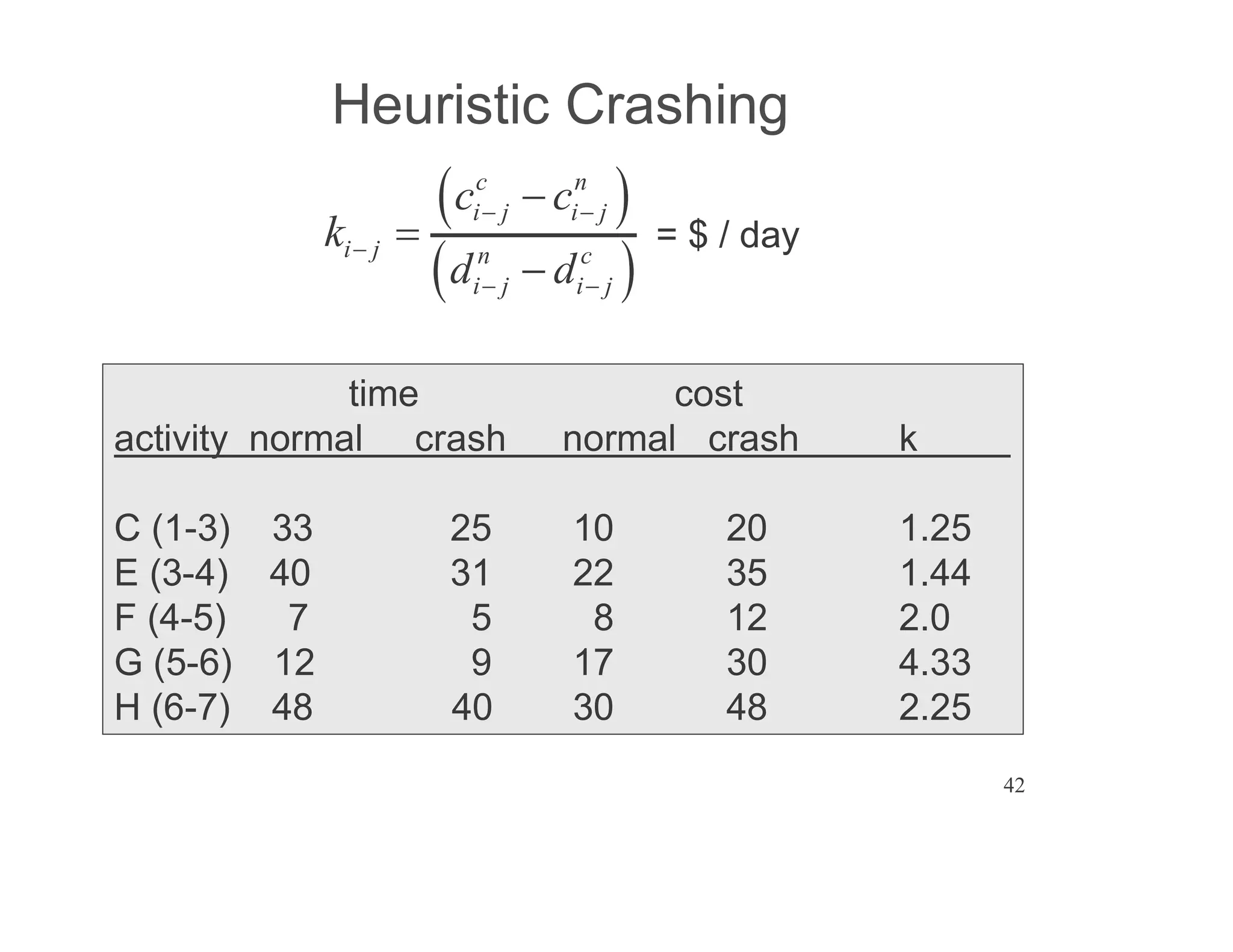
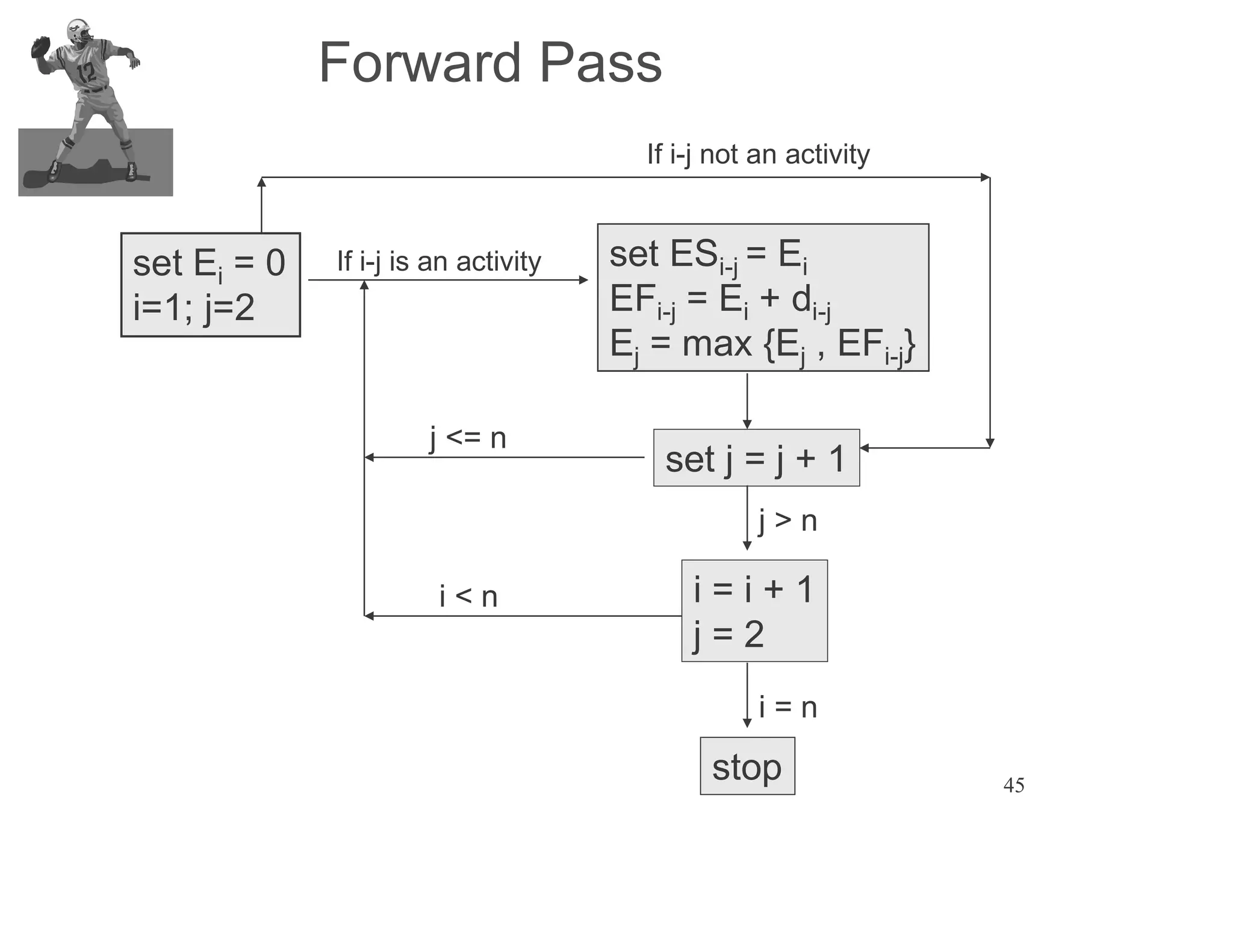
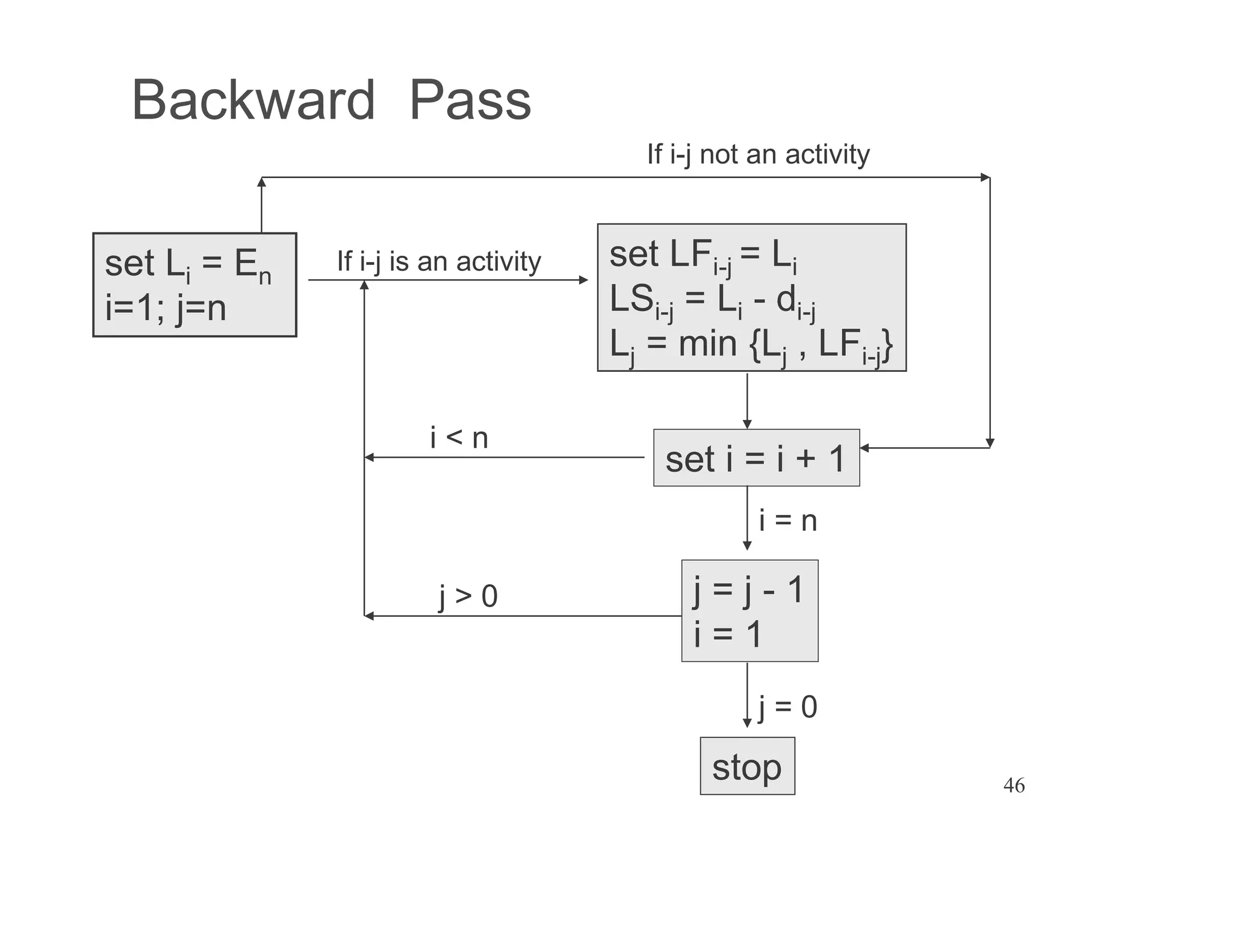
The document presents an extensive framework for project planning, scheduling, and control, emphasizing the significance of network models like Pert and CPM. It details the elements of project scheduling, definitions of key terms, network representation, critical path analysis, and methods for determining time-cost trade-offs. Furthermore, it provides examples and methodologies for analyzing project activities, managing resources, and addressing constraints to optimize project completion.

1. UNIT 4
System Schedule
ME 342 A
System Design and Analysis
Dr. Kailash Chaudhary
Ph.D. (Mechanical Design), M.E. (P & I), B.E. (Mechanical Engg)
Assistant Professor
Department of Mechanical Engineering
MBM University Jodhpur

2. 2
Project Planning, Scheduling and Control
Project a set of partially ordered,
interrelated activities that must be
completed to achieve a goal.

3. 3
Network Models
PERT Program Evaluation and Review
Technique
probabilistic features
CPM Critical Path Method
cost/time trade-offs
project scheduler

4. 4
Objectives
Planning, scheduling, and control of complex
projects
Find critical activities to manage resources
(management by exception)
Determine flexibility of non-critical activities
(slack)
Estimate earliest completion time of project
Determine time cost trade-offs

5. 5
Service
Industry
Distribution
Industry
Producing
Industry
Business and Industry a taxonomy
Raw
materials
Continuous
Processing
Discrete
Products
Mining
Drilling
Farming
Construction Manufacturing Chemicals
Food
Refinery
Batch Mass
Processing Production

6. 6
Production Systems
Job shops
Flow shops
Batch production
Mass production
Cellular manufacturing
Project Shop
Continuous Processing
Gosh. Can you
tell us more
about these?

7. 7
Project Shop
single product in fixed location
material and labor brought to the site
usually job shop/flow shop associated
functionalized production system
examples include construction and
shipbuilding

8. 8
The Elements of Project Scheduling
Project Definition. Statement of project, goals, and
resources required.
Activity Definitions. Content and requirements of
each activity.
Project Scheduling. Specification of starting and
ending times of all activities.
Project Monitoring. Keeping track of the progress of
the project.

9. 9
Definitions
Activity an effort (task) that requires resources and
takes a certain amount of time.
Event a specific accomplishment or milestone (the
start or finish of an activity).
Project a collection of activities and events leading
to a definable goal.
Network a graphical representation of a project
depicting the precedence relationships among the
activities and events.
Critical Activity an activity that if delayed will hold
up the scheduled completion of a project.
Critical Path the sequence of critical activities that
forms a continuous path from the start of a project to
its completion.

10. 10
Framework for Analysis
Analyze project in terms of activities and
events
Determine sequence (precedence) of
activities (develop network)
Assign estimates of time, cost, and resources
to all activities
Identify the critical path
monitor, evaluate, and control progress of
project

11. 11
Network Representation
Projects may be represented as networks with:
Arrows representing activities.
Nodes representing completion of a set of activities
(milestones).
Pseudo activities may be required to satisfy
precedence relationships.

12. 12
Network Development
1 2 3
events
(nodes)
activities
(arcs)
Activities have duration
and may have precedence.
Define activities in terms of
their beginning and ending events.
e.g. Activity 1-2 must precede Activity 2-3

13. 13
Network Development (continued)
1
2
3
4
Event 1 is start of project
Activities 1-2, 1-3, and
1-4 have no predecessors
and may start simultaneously

14. 14
Network Development (continued)
n-2
n-3
n
n-1
Event n is the end of the
project. Activities (n-3 n,
(n-2) n, and (n-1) - n
must be completed for the
project to be completed.

15. 15
Network Development (continued)
6
7
8
9
Activities 6-7, 6-8, and
6-9 cannot start until activity 5-6
has been completed.
5
burst event

16. 16
Network Development (continued)
8
5
6
7
Activities 5-8, 6-8, and
7-8 must be completed
before activity 8-9 may begin.
9
merge event

17. 17
Network Development (continued)
8
5
6
7
Activities 5-8, 6-8, and 7-8 must be completed
before activity 8-9, 8-10, or 8-11 may begin.
9
10
11
Gosh! A
combined
merge and
burst event.
Are these
rare or what?

18. 18
Dummy activity
A C
A D
B D
W R O N G
7
5
6
9
10
A
B
C
D
7
5
6
9
10
A
B D
C
8
dummy has no resources and no duration

19. 19
Project Networks
Collection of nodes and arcs
Depicted graphically
Events are uniquely numbered
Arcs are labeled according to their beginning and
ending events
Ending events always have higher numbers than beginning
events
Two activities cannot have the same beginning and
ending events
Activity lengths have no significance

20. 20
Our Very Own Example
product development
activity description precedence
A design promotion campaign -
B initial pricing -
C product design -
D promotion cost analysis A
E manufacture prototype C
F test and redesign E
G final pricing B,D,F
H market test G

21. 21
product development
1
2
3 4
6 7
5
A
B
C
D
E
F
G H

22. 22
Notation
i-j = an activity of a project
di-j = the duration of activity i-j
Ei = the earliest time event i can occur
ESi-j = the earliest start time of activity i-j
EFi-j = the earliest finish time of activity i-j
LSi-j = the latest start time of activity i-j
LFi-j = the latest finish time of activity i-j
Li = the latest time event i can occur

23. 23
Our Very Own Example
product development
activity precedence duration (days)
A (1-2) - 17
B (1-5) - 7
C (1-3) - 33
D (2-5) A 6
E (3-4) C 40
F (4-5) E 7
G (5-6) B,D,F 12
H (6-7) G 48

24. 24
product development forward pass
1
2
3 4
6 7
5
A(17)
B(7)
C(33)
D(6)
E(40)
F(7)
G(12) H(48)
E1 = 0
ES1-2 = 0
ES1-5 = 0
ES1-3 = 0
EF1-2 = 17
EF1-5 = 7
EF1-3 = 33
E2 = 17
E5 = 7
E3 = 33
ES5-6 = 80
EF5-6 = 92
E6 = 92
ES2-5 = 17
ES3-4 = 33
EF2-5 = 23
EF3-4 = 73
E4 = 73
ES4-5 = 73
EF4-5 = 80 E5 = 80
ES6-7 = 92
EF6-7 = 140
E7 = 140

25. 25
product development backward pass
1
2
3 4
6 7
5
A(17)
B(7)
C(33)
D(6)
E(40)
F(7)
G(12) H(48)
L1 = 0
LF1-2 = 74
LF1-5 = 80
LF1-3 = 33
L2 = 74
L3 = 33
L6 = 92
LF5-6 = 92
LS5-6 = 80
LF2-5 = 80
LS2-5 = 74
LF3-4 = 73
LS3-4 = 33
L4 = 73
LF4-5 = 80
LS4-5 = 73
L5 = 80
L7 = 140
LF6-7 = 140
LS6-7 = 92
LS1-2 = 57
LS1-5 = 73
LS1-3 = 0

26. 26
Activity Slack
Si-j = LSi-j ESi-j Si-j = LFi-j EFi-j
or
Activity LS ES Slack
1-2 57 0 57
1-5 73 0 73
1-3 0 0 0
2-5 74 17 57
3-4 33 33 0
4-5 73 73 0
5-6 80 80 0
6-7 92 92 0
critical
activities

27. 27
Critical Path Method
An analytical tool that provides a schedule that
completes the project in minimum time subject to the
precedence constraints. In addition, CPM provides:
Starting and ending times for each activity
Identification of the critical activities (i.e., the ones
whose delay necessarily delay the project).
Identification of the non-critical activities, and the
amount of slack time available when scheduling
these activities.

28. 28
critical path
1
2
3 4
6 7
5
A(17)
B(7)
C(33)
D(6)
E(40)
F(7)
G(12) H(48)
ES1-3 = 0
LS1-3 = 0
ES5-6 = 80
LS5-6 = 80
ES3-4 = 33
LS3-4 = 33
ES4-5 = 73
LS4-5 = 73
ES6-7 = 92
LS6-7 = 92
ES1-5 = 0
LS1-5 = 73
ES2-5 = 17
LS2-5 = 74
ES1-2 = 0
LS1-2 = 57

29. 29
Critical Path Activities
focus management attention
increase resources
eliminate delays
eliminate critical activities
overlap critical activities
break activity into smaller tasks
outsource or subcontract

30. 30
Critical Path by LP
1
Min
. :
, pairs
n
n
i
j i ij
E
subj to
E E d i j
earliest start times
1
1
Min
. :
, pairs
n
n i
i
j i ij
nL L
subj to
L L d i j
latest start times

31. 31
Activity Durations
a b
uniform
triangular
beta

32. 32
More Activity Durations
let a = optimistic time
b = pessimistic time
m = most likely time
2
2
2 12
a b b a
2 2 2
2
3 18
a m b a b m ab am bm
2
2
4
6 18
a m b b a
uniform:
triangular:
beta:

33. 33
activity durations
product development
activity a m b
A (1-2) 6 18 24 17 9 3
B (1-5) 6 6 12 7 1 1
C (1-3) 24 30 54 33 25 5
D (2-5) 6 6 6 6 0 0
E (3-4) 24 36 72 40 64 8
F (4-5) 6 6 12 7 1 1
G (5-6) 6 12 18 12 4 2
H (6-7) 36 48 60 48 16 4
2
beta
note: based upon a 6 day workweek

34. 34
critical path analysis
product development
activity a m b
C (1-3) 24 30 54 33 25 5
E (3-4) 24 36 72 40 64 8
F (4-5) 6 6 12 7 1 1
G (5-6) 6 12 18 12 4 2
H (6-7) 36 48 60 48 16 4
sum 140 110
2
beta
From the Central Limit Theorem, project completion
time is normally distributed with a mean of 140 days
and a standard deviation of = 10.5 days.
110

35. 35
Probability Statements
Probability project will be completed by day 150 is
given by:
150 140
Pr 150 Pr Pr .95 .829
10.5
T
T z
Probability project will be completed after day 130
is given by:
130 140
Pr 130 Pr Pr .95 .171
10.5
T
T z

36. 36
Resource Constraints
Activity ES Duration staffing
1-2 0 17 5
1-5 0 7 7
1-3 0 33 10
2-5 17 6 4
3-4 33 40 6
4-5 73 7 3
5-6 80 12 5
6-7 92 48 6

37. 37
Resource Profile early start schedule
0 10 20 30 40 50 60 70 80
30
25
20
15
10
5
1-2
1-5
1-3
3-4
2-5
4-5 5-6
We need too many
people at the start
of the project!

38. 38
Late Start Staffing
Activity ES Duration staffing
1-2 57 17 5
1-5 73 7 7
1-3 0 33 10
2-5 74 6 4
3-4 33 40 6
4-5 73 7 3
5-6 80 12 5
6-7 92 48 6

39. 39
Resource Profile late start schedule
0 10 20 30 40 50 60 70 80
30
25
20
15
10
5
1-2
1-5
1-3
3-4
2-5
4-5 5-6
the late start schedule.
Then we can layoff
some folks.

40. 40
Time Costing Methods
Suppose that projects can be expedited by
reducing the time required for critical activities.
Doing so results in an increase in some costs
and a decrease in others. The goal is to
determine the optimal number of days to
schedule the project to minimize total cost.
Assume that there is a linear time/cost
relationship for each activity.

41. 41
Time-Cost Trade-offs
time
crash
time
normal
time
crash
cost
normal
cost
,
n n
i j i j
d c
,
c c
i j i j
d c

42. 42
Heuristic Crashing
c n
i j i j
i j n c
i j i j
c c
k
d d
= $ / day
time cost
activity normal crash normal crash k
C (1-3) 33 25 10 20 1.25
E (3-4) 40 31 22 35 1.44
F (4-5) 7 5 8 12 2.0
G (5-6) 12 9 17 30 4.33
H (6-7) 48 40 30 48 2.25

43. 43
An LP approach
let yi-j = number of time units activity i-j is crashed
K = indirect cost per day
,
min
. :
0
0 1,2,...,
i j i j n
all i j
n
j i i j i j
n c
i j i j i j
i
k y K E
subt to
E E y d i j
y d d i j
E i n

44. 44
The End
Backups Follow

45. 45
Forward Pass
set Ei = 0
i=1; j=2
set ESi-j = Ei
EFi-j = Ei + di-j
Ej = max {Ej , EFi-j}
If i-j is an activity
set j = j + 1
j <= n
i = i + 1
j = 2
j > n
i < n
stop
i = n
If i-j not an activity

46. 46
Backward Pass
set Li = En
i=1; j=n
set LFi-j = Li
LSi-j = Li - di-j
Lj = min {Lj , LFi-j}
If i-j is an activity
set i = i + 1
i < n
j = j - 1
i = 1
i = n
j > 0
stop
j = 0
If i-j not an activity