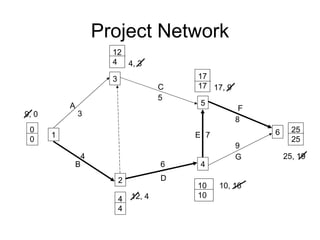
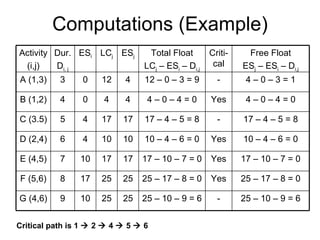
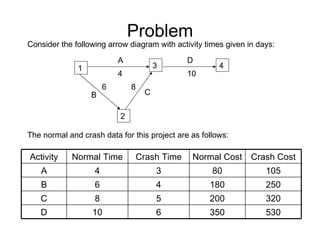
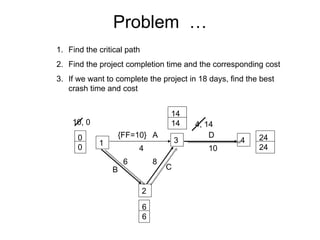
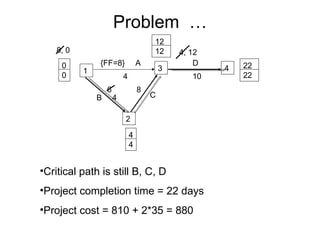
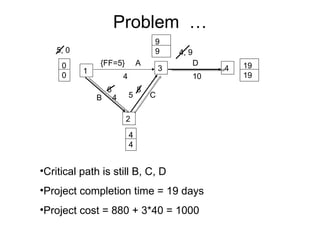
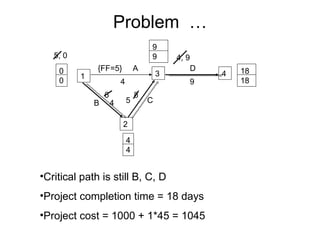
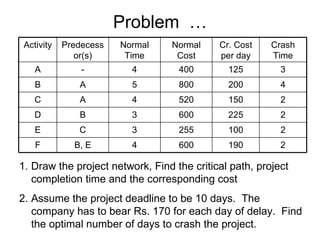
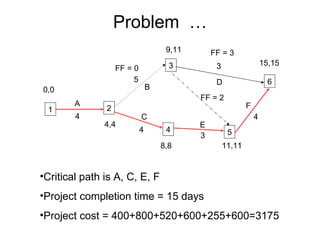
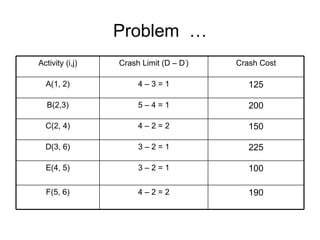
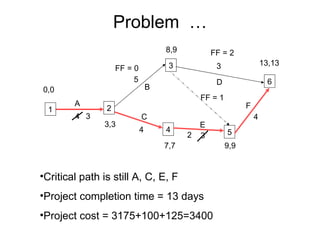
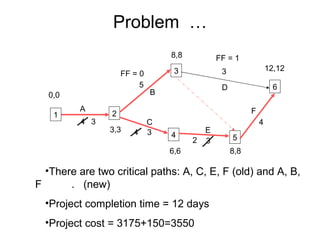
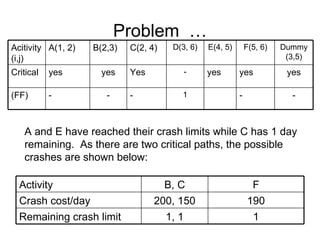
The document discusses graphs, networks, project scheduling, critical path method (CPM), program evaluation and review technique (PERT), activity-on-node (AON) and activity-on-arc (AOA) representations, activity slack, floats, crashing activities to reduce project duration, and performing time-cost tradeoffs to optimize project costs. It provides definitions of key terms like vertices, edges, predecessors, successors, critical and non-critical activities, earliest start times, latest completion times, total float and free float. It also includes an example problem demonstrating how to construct a network diagram, find the critical path, compute activity times, and determine the optimal crash time and costs to meet a deadline.