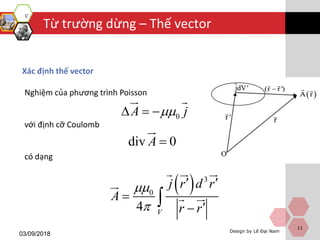
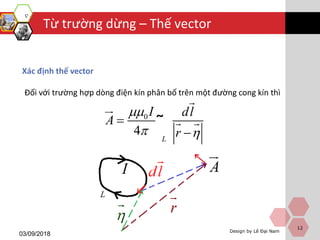
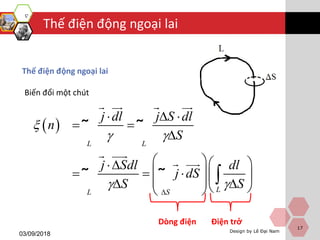
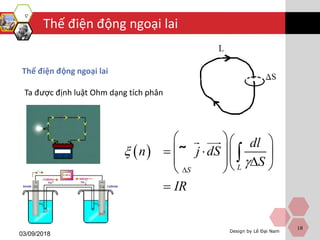
Tài liệu trình bày về từ trường dừng, định nghĩa và các phương trình liên quan, bao gồm lĩnh vực điện từ và thế vector. Nó giải thích khái niệm từ trường dừng cũng như các phương trình Poisson mô tả thế vector của nó. Cuối cùng, tài liệu nêu lên năng lượng của dòng dừng và các bài tập luyện tập liên quan.