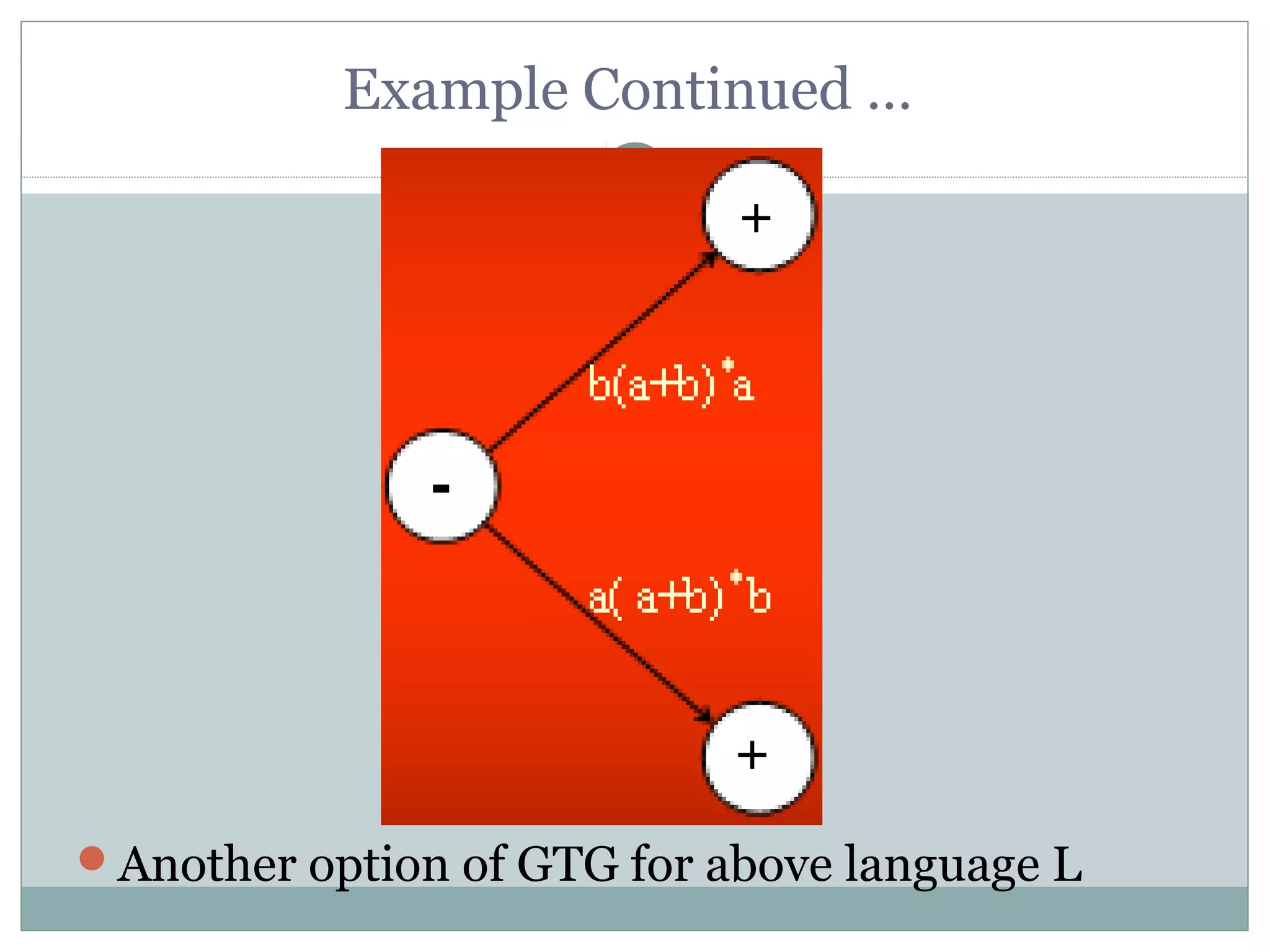
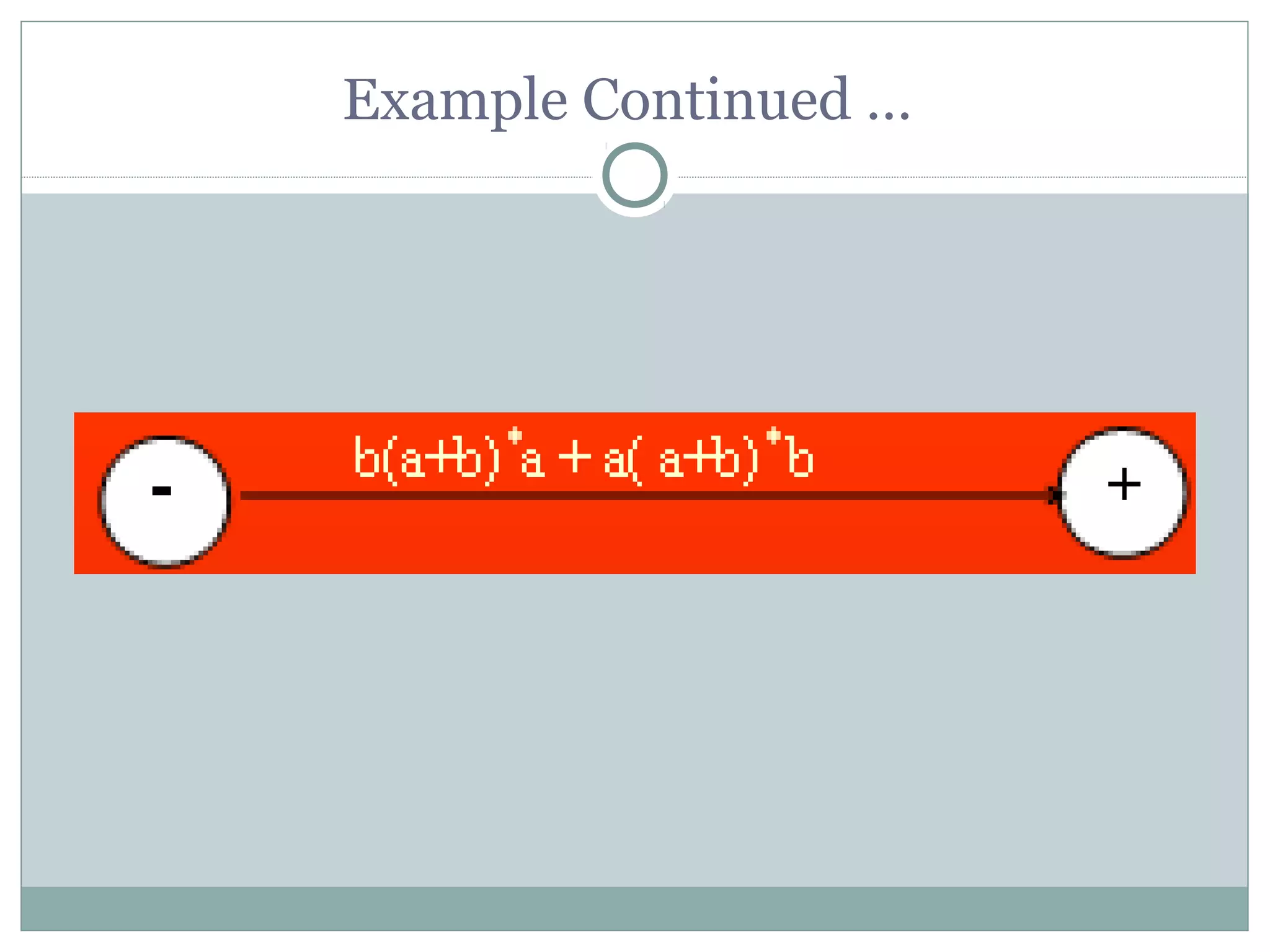
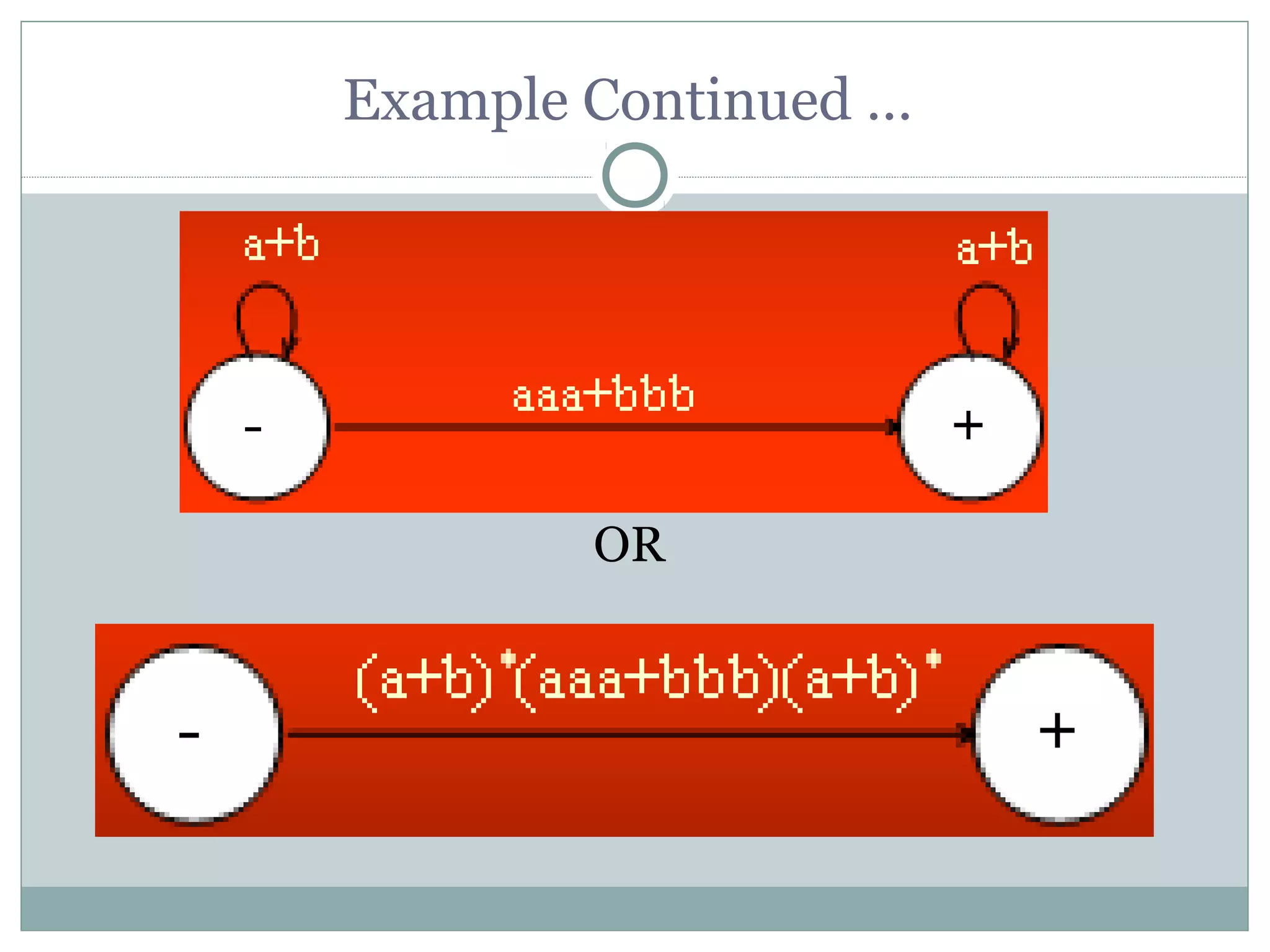
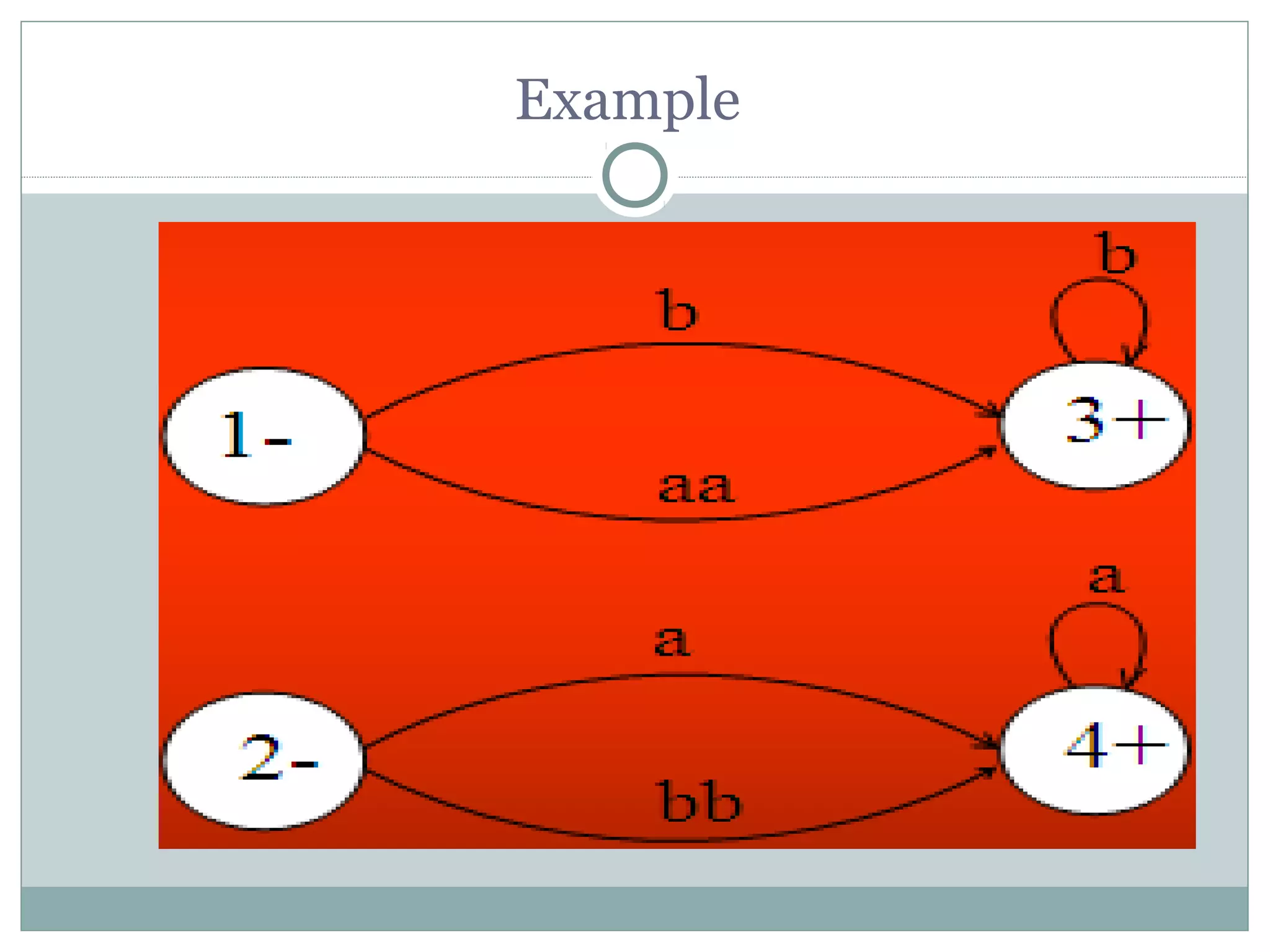
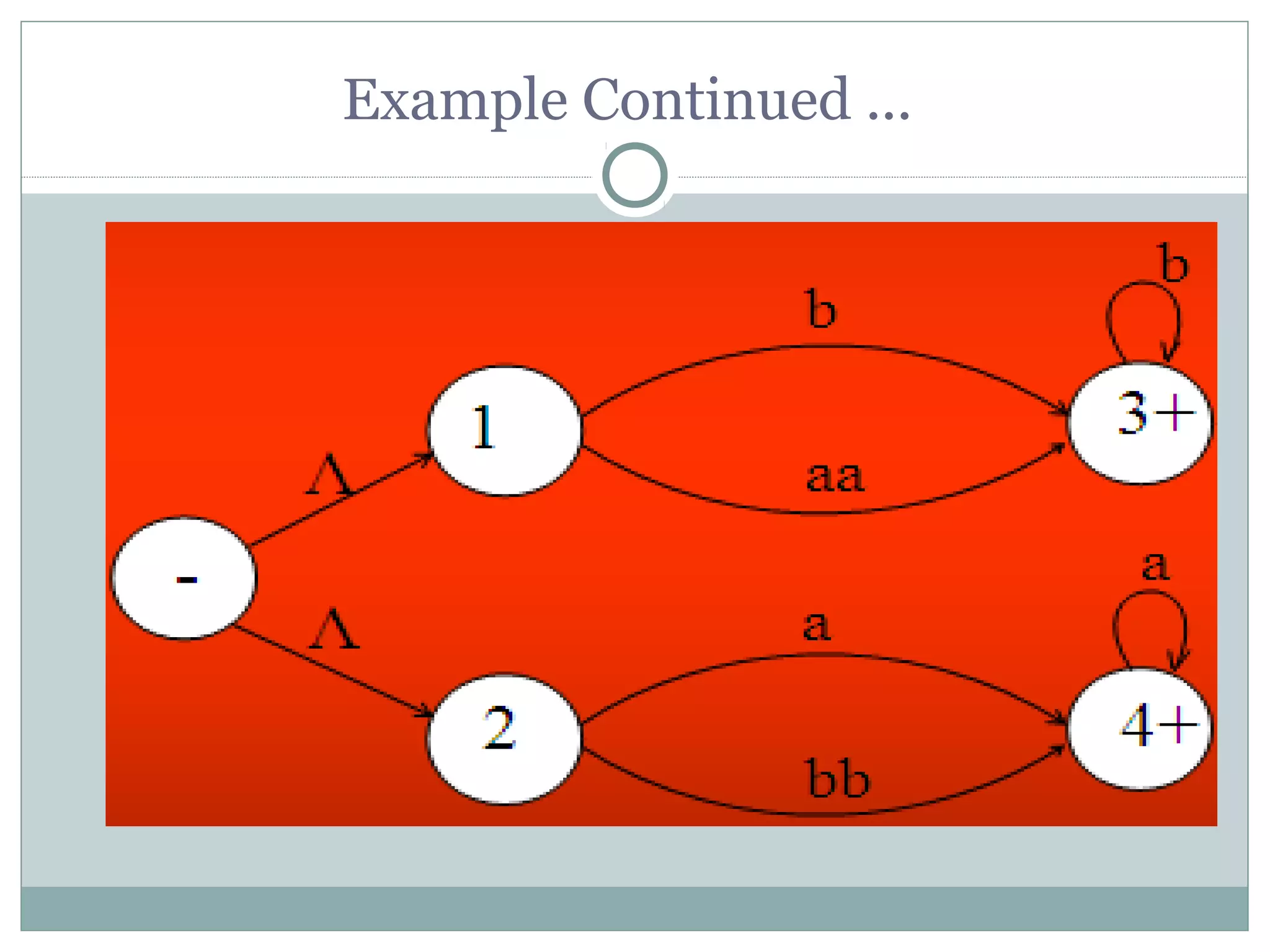
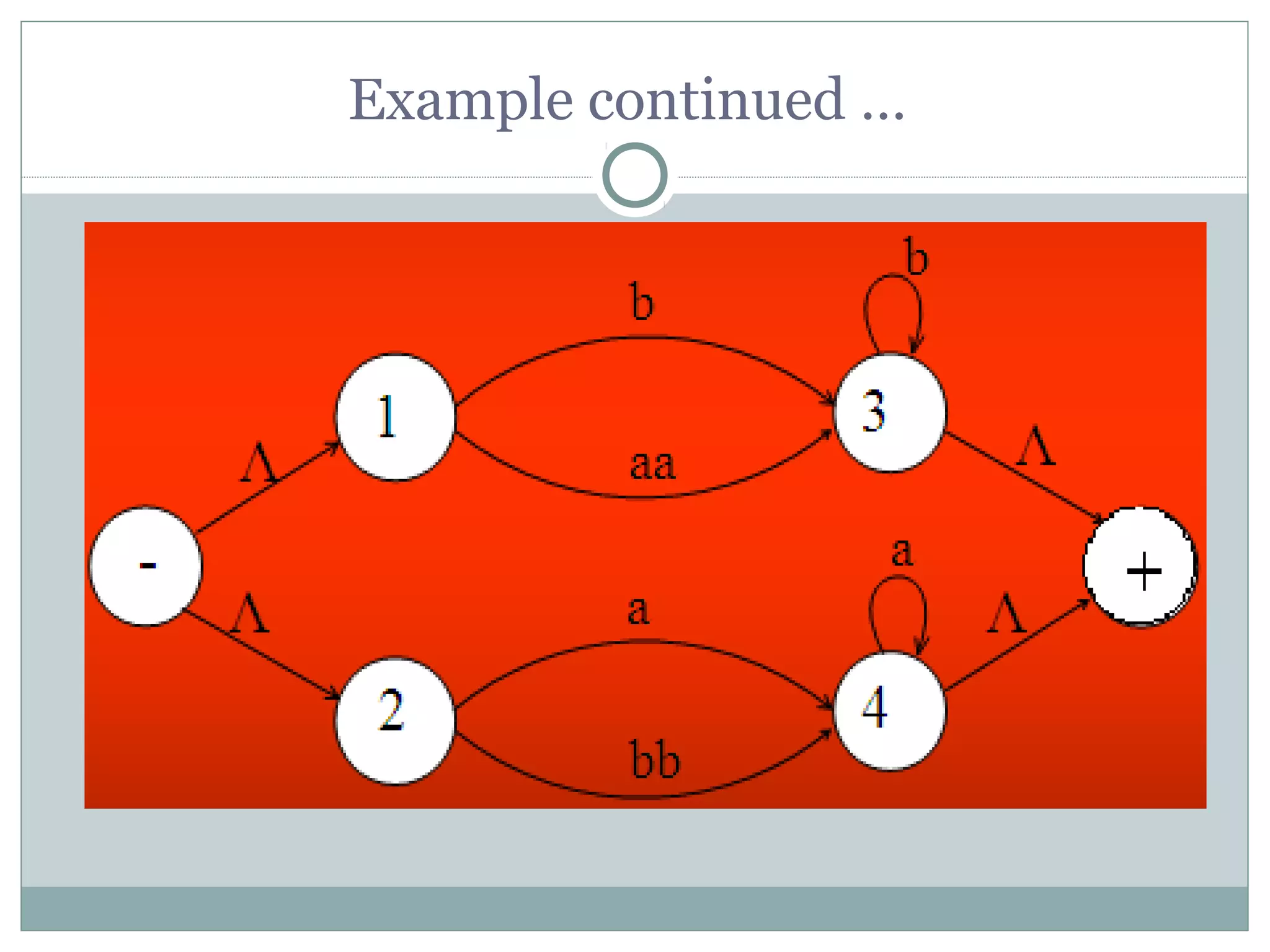
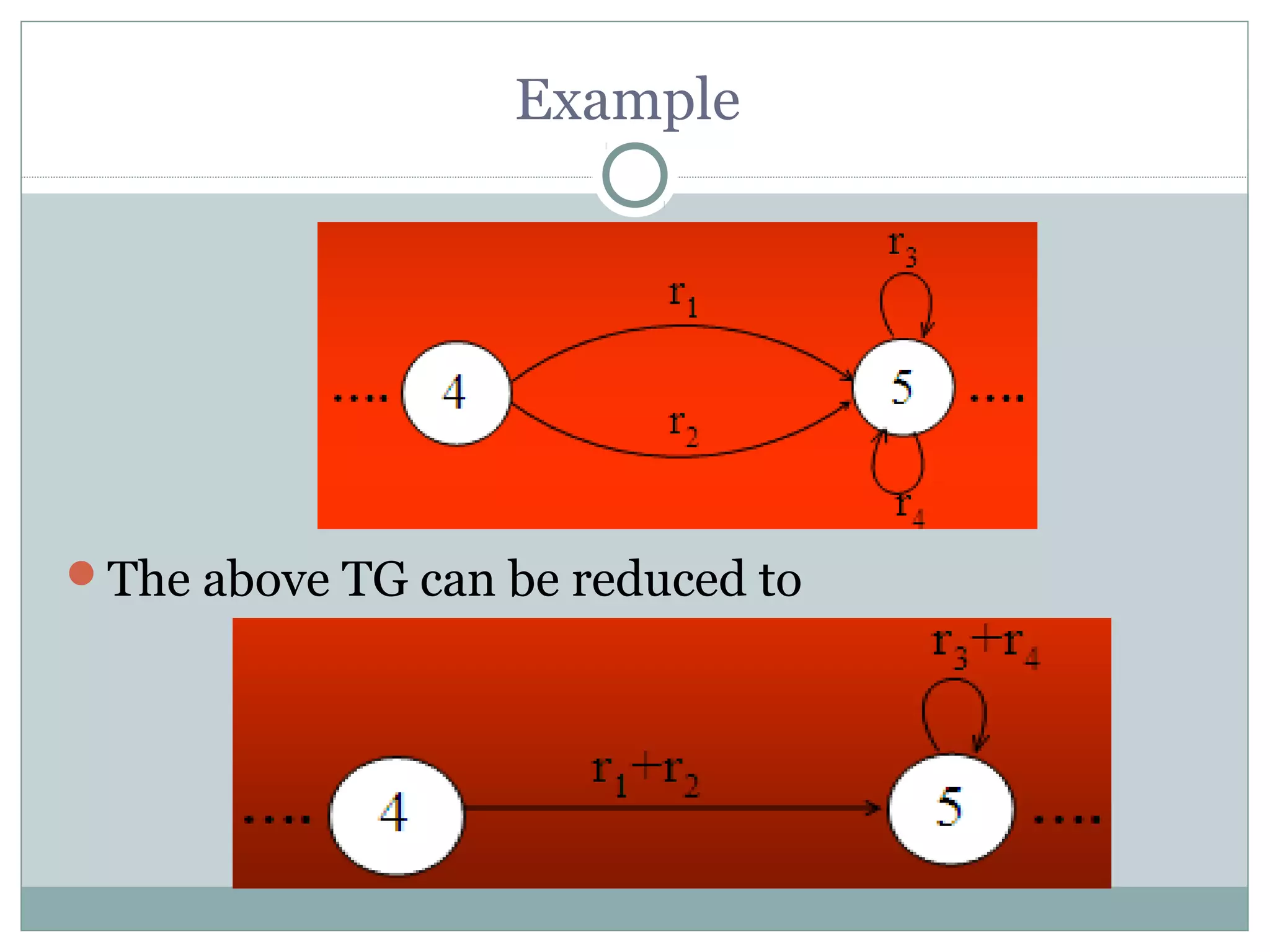
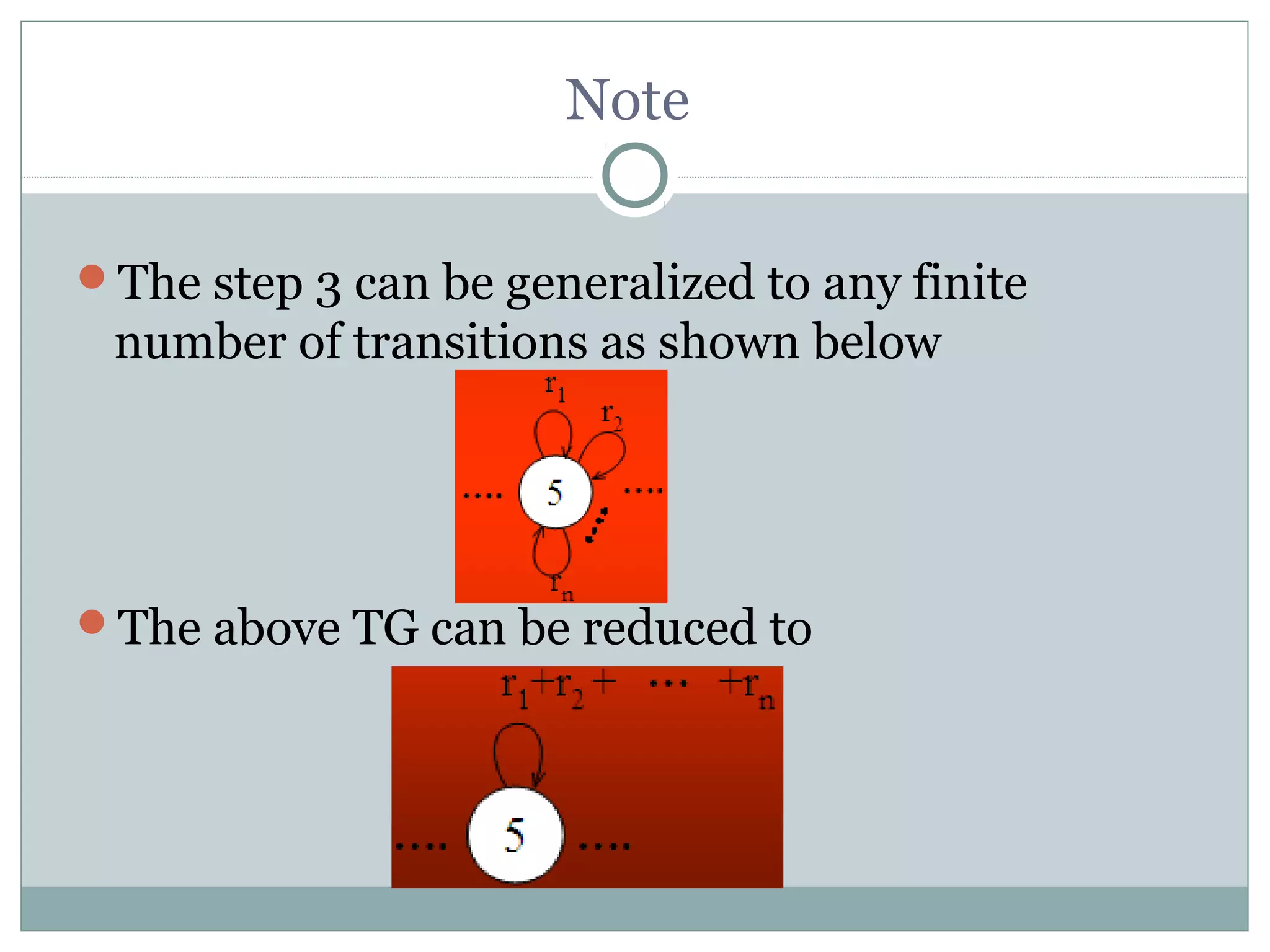
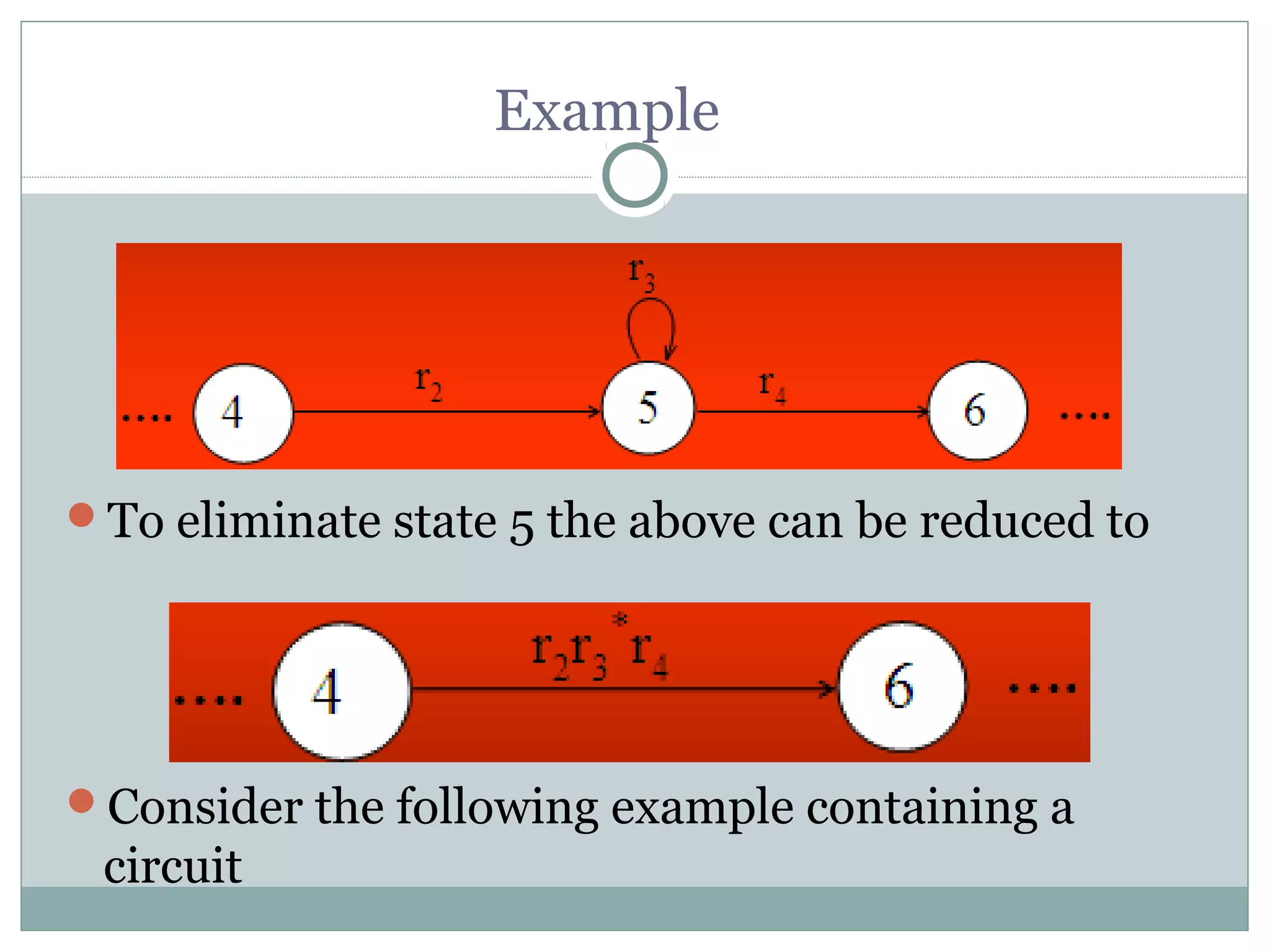
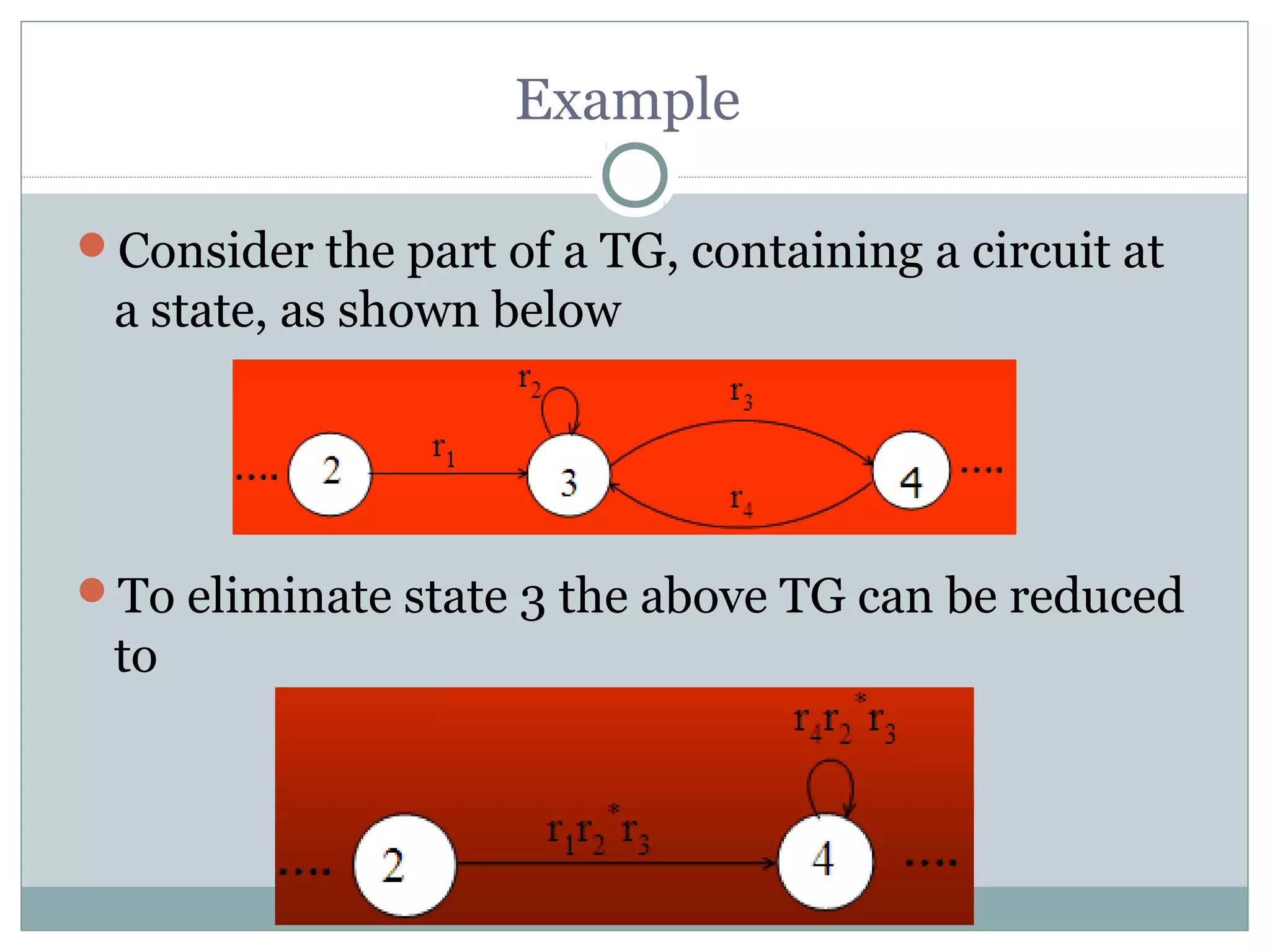
This document summarizes lecture material on automata theory and formal languages. It provides examples of languages defined over the alphabet {a,b} that can be expressed using regular expressions and accepted by generalized transition graphs. Kleene's theorem is also discussed, which states that a language can be expressed using finite automata, transition graphs, or regular expressions if and only if it can be expressed using the other two as well. The proof of Kleene's theorem is outlined in three parts: 1) A language accepted by a finite automaton can be accepted by a transition graph; 2) A language accepted by a transition graph can be expressed with a regular expression; and 3) A language expressed by a regular expression can be accepted by