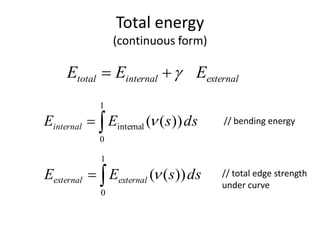
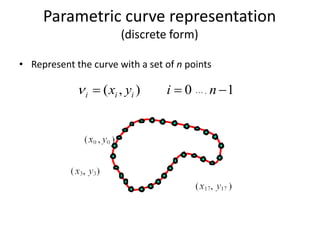
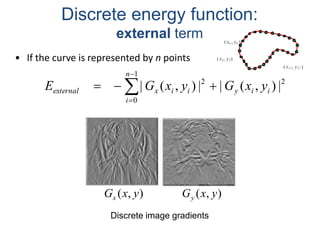
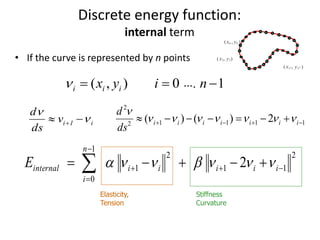
The document provides an overview of computer vision techniques including edge detection, edge representation using chain codes, line and circle detection using Hough transforms, and active contour deformable models (snakes). It describes several common edge detection algorithms like Prewitt, Laplacian of Gaussian (LoG), and Canny edge detectors. It also explains how the Hough transform can be used to detect lines and circles and discusses snakes, where an active contour model is defined as an energy minimizing spline that deforms to fit desired image properties by minimizing internal and external energy terms.

1. Computer Vision
SBE 404, Spring 2020
Professor
Ahmed M. Badawi
ambadawi@eng1.cu.edu.eg
http://scholar.google.com.eg/citations?user=r9pLu6EAAAAJ&hl=en
http://www.bmes.cufe.edu.eg
TA’s:
Eman Marzban
eman.marzban@eng1.cu.edu.eg
Asem Abdelaziz
asem.a.abdelaziz@eng1.cu.edu.eg

2. 3/19/2020 2
Overview
1.Edge Detection
2.Edge Representation using Chain Codes
3.Line and Circle Detection using Hough
Transforms
4.Active contour deformable model
(Snakes)

3. 3/19/2020 3
Edge Detection Goal: Could you point out the most “salient” or “strongest” edges or
the object boundaries? [Szeliski's Book p.210]

4. 3/19/2020 4
-Qualitatively, edges occur at boundaries between regions of
different color, intensity, or texture.
-Define an edge as a location of rapid intensity variation.
-Think of an image as a height field. On such a surface, edges
occur at locations of steep slopes.
- A mathematical way to define the slope and direction of a
surface is through its gradient,
- The local gradient vector J points in the direction of steepest
ascent in the intensity function. Its magnitude is an indication of
the slope or strength of the variation, while its orientation
points in a direction perpendicular to the local contour.
How can we basically detect an edge?

5. 3/19/2020 5
[Ch. 14, Practical Image and Video Processing Using MATLAB by Oge Marques]

6. 3/19/2020 6
- Beware of the image noise! Smooth the image with a low-pass
filter prior to computing the gradient.
-The gradient of the smoothed image can therefore be written as
i.e., we can convolve the image with the horizontal and vertical
derivatives of the Gaussian kernel function,
Handling image noise in edge detection

7. 3/19/2020 7
[Ch. 14,
Practical
Image
and Video
Processin
g Using
MATLAB
by Oge
Marques]
Even low noise levels can corrupt the edge detection operation…

8. 3/19/2020 8
- For many applications, we wish to thin such a continuous
gradient image to only return isolated edges, i.e., as single pixels
at discrete locations along the edge contours.
-This can be achieved by looking for maxima in the edge strength
(gradient magnitude) in a direction perpendicular to the edge
orientation, i.e., along the gradient direction.
-Finding this maximum corresponds to taking a directional
derivative of the strength field in the direction of the gradient and
then looking for zero crossings.
- The desired directional derivative is equivalent to the dot
product between a second gradient operator and the results
of the first,
Thinning the gradient image

9. 3/19/2020 9
-The gradient operator dot product with the gradient is called the
Laplacian. The convolution kernel
is therefore called the Laplacian of Gaussian (LoG) kernel. This
kernel can be split into two separable parts,
which allows for a much more efficient implementation
using separable filtering.
Thinning the gradient image (continued)

10. 3/19/2020 10
[Ch. 14,
Practical
Image and
Video
Processing
Using
MATLAB by
Oge
Marques]

11. 3/19/2020 11
- Estimate the gray-level gradient at a pixel, which can be approximated by the
digital equivalent of the first-order derivative as follows [Marques’ book, p.338]:
- The gradients are often computed within a 3×3 neighborhood using convolution:
where the Prewitt kernels are given by:
Example 1: Prewitt Edge Detector (First-order
Detector)

12. 3/19/2020 12
[Ch. 14,
Practical
Image
and
Video
Processi
ng Using
MATLAB
by Oge
Marque
s]

13. 3/19/2020 13
- The Laplacian operator is a straightforward digital
approximation of the second-order derivative of the intensity.
Although it has the potential for being employed as an isotropic
(i.e., omnidirectional) edge detector, it is rarely used in isolation
because of two limitations [Marques’ book, p. 343]:
• It generates “double edges,” that is, positive and negative
values for each edge.
• It is extremely sensitive to noise.
Example 2: Zero-crossing Edge Detector
(Second-order detector)

14. 3/19/2020 14
[Ch. 14,
Practical
Image
and
Video
Processi
ng Using
MATLAB
by Oge
Marque
s]

15. 3/19/2020 15
- The Laplacian of Gaussian (LoG) edge detector works by
smoothing the image with a Gaussian low-pass filter (LPF), and
then applying a Laplacian edge detector to the
result.
- David Marr and Ellen Hildreth proposed that LoG filtering
explains much of the low-level behavior of the human vision
system, since the response profile of an LoG filter approximates
the receptive field of retinal cells tuned to respond to edges.
Example 3: Laplacian-of-Gaussian Edge
Detector (Second-order detector)

16. 3/19/2020 16
[Ch. 14,
Practical
Image
and
Video
Processi
ng Using
MATLAB
by Oge
Marque
s]

17. 3/19/2020 17
[Ch. 14,
Practical
Image
and
Video
Processi
ng Using
MATLAB
by Oge
Marque
s]

18. 3/19/2020 18
1. The input image is smoothed using a Gaussian low-pass filter, with a
specified value of σ: large values of σ will suppress much of the noise at
the expense of weakening potentially relevant edges.
2. The local gradient (intensity and direction) is computed for each point in
the smoothed image.
3. The edge points at the output of step 2 result in wide ridges. The
algorithm thins those ridges, leaving only the pixels at the top of each
ridge, in a process known as nonmaximal suppression.
4. The ridge pixels are then thresholded using two thresholds Tlow and Thigh:
ridge pixels with values greater than Thigh are considered strong edge
pixels; ridge pixels with values between Tlow and Thigh are said to be weak
pixels. This process is known as hysteresis thresholding.
5. The algorithm performs edge linking, aggregating weak pixels that are 8-
connected to the strong pixels.
Example 4: Canny Edge Detector

19. 3/19/2020 19
Canny Edge Detection
http://www.cse.iitd.ernet.in/~pkalra/csl783/canny.pdf

20. 3/19/2020 20
[Ch. 14,
Practical
Image
and
Video
Processi
ng Using
MATLAB
by Oge
Marque
s]

21. 3/19/2020 21
Study and Comparison of
Various Image Edge Detection
Techniques
Raman Maini, Himanshu
Aggarwal
http://www.cscjournals.org/cs
c/download/issuearchive/IJIP/
volume3/IJIP_V3_I1.pdf

22. 3/19/2020 22
Overview
1.Edge Detection
2.Edge Representation using Chain
Codes
3.Line and Circle Detection using Hough
Transforms
4.Active contour deformable model
(Snakes)

23. 3/19/2020 23
Edge Representation using Chain Codes [Szeliski's Book p.217]
- Linked edgel lists can be encoded more compactly using a variety of alternative
representations.
A chain code encodes a list of connected points lying on an N-8 grid using a
three-bit code corresponding to the eight cardinal directions (N, NE, E, SE, S, SW, W, NW)
between a point and its successor (Figure 4.34).
-While this representation is more compact than the original edgel list (especially if
predictive variable-length coding is used), it is not very suitable for further processing.
-See: Introduction to Chain Codes
http://www.mind.ilstu.edu/curriculum/chain_codes_intro/chain_codes_intro.php

24. 3/19/2020 24
Edge Representation using Chain Codes
- Chain code examples http://www.eng.iastate.edu/ee528/sonkamaterial/chapter_3.htm
http://www.cs.ru.nl/~ths/rt2/col/h9/9ge
biedENG.html

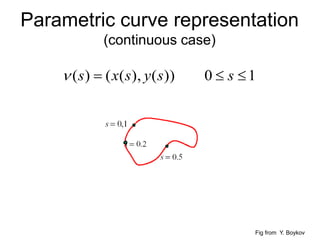
25. 3/19/2020 25
Edge Representation using Arc-Length Parameterization [Szeliski's Book p.217]
- A more useful representation is the arc length parameterization of a contour, x(s), where
s denotes the arc length along a curve (Figure 4.35).

26. 3/19/2020 26
Edge Representation using Arc-Length Parameterization [Szeliski's Book p.217]
- The advantage of the arc-length parameterization is that it makes matching and
processing (e.g., smoothing) operations much easier (Figure 4.36). Arc-length
parameterization can also be used to smooth curves in order to remove digitization noise.

27. 3/19/2020 27
Overview
1.Edge Detection
2.Edge Representation using Chain Codes
3.Line and Circle Detection using Hough
Transforms
4.Active contour deformable model
(Snakes)

28. 3/19/2020 28
Points and lines
in image and
parameter spaces
http://books.google.com.eg/books/abou
t/Digital_Image_Processing.html?id=jCEi
9MVfxD8C&redir_esc=y
[Chapter 9]

29. 3/19/2020 29

30. 3/19/2020 30
Line Detection using Hough Tranform [Szeliski's Book p.221]
Motivation: Lines in the real world are sometimes broken up into disconnected
components or made up of many collinear line segments. In many cases, it is desirable to
group such collinear segments into extended lines.
Original Formulation: Each edge point votes for all possible lines passing through it, and
lines corresponding to high accumulator or bin values are examined for potential line fits.

31. 3/19/2020 31
Line Detection using Hough Tranform [Szeliski's Book p.222]
Alternate Formulation: Use the local orientation information at each edgel
to vote for a single accumulator cell.

32. 3/19/2020 32
Line Detection using Hough Tranform [Szeliski's Book p.223]

33. 3/19/2020 33
Hough Transform for Circles

34. 3/19/2020 34
Hough Transform for General Parametric Curves

35. 3/19/2020 35
Overview
1.Edge Detection
2.Edge Representation using Chain Codes
3.Line and Circle Detection using Hough
Transforms
4.Active contour model (Snakes)

36. 3/19/2020 36
Image Segmentation using the Snake Active
Contour Model

37. 3/19/2020 37
- The active contour model, or snake, is defined as an energy minimizing spline
- The snake's energy depends on its shape and location within the image.
- Local minima of this energy then correspond to desired image properties.
- Snakes may be understood as a special case of a more general technique of
matching a deformable model to an image by means of energy minimization.
- Snakes do not solve the entire problem of finding contours in images, but
rather, they depend on other mechanisms like interaction with a user,
interaction with some higher level image understanding process, or information
from image data adjacent in time or space.
- This interaction must specify an approximate shape and starting position for
the snake somewhere near the desired contour.
-A priori information is then used to push the snake toward an appropriate
solution.
- The energy functional which is minimized is a weighted combination of
internal and external forces.
- The internal forces emanate from the shape of the snake, while the external
forces come from the image and/or from higher level image understanding
processes.
http://www.engineering.uiowa.edu/~dip/LECTURE/Understanding2.html

38. 3/19/2020 38
Deformable model (Snakes)

39. Deformable contours
Given: initial contour (model) near desired object
a.k.a. active contours, snakes
(Single frame)
Fig: Y. Boykov
[Snakes: Active contour models, Kass, Witkin, & Terzopoulos, ICCV1987]

40. Deformable contours
Given: initial contour (model) near desired object
a.k.a. active contours, snakes
(Single frame)
Fig: Y. Boykov
Goal: evolve the contour to fit exact object boundary
[Snakes: Active contour models, Kass, Witkin, & Terzopoulos, ICCV1987]

41. Deformable contours
initial intermediate final
a.k.a. active contours, snakes
Fig: Y. Boykov
Initialize near contour of interest
Iteratively refine: elastic band is adjusted so as to
• be near image positions with high gradients, and
• satisfy shape “preferences” or contour priors

42. Deformable contours
initial intermediate final
a.k.a. active contours, snakes
Like generalized Hough transform, useful for shape fitting; but
Hough
Fixed model shape
Single voting pass can
detect multiple instances
Snakes
Prior on shape types, but shape
iteratively adjusted (deforms)
Requires initialization nearby
One optimization “pass” to fit a
single contour

43. Why do we want to fit deformable
shapes?
• Non-rigid,
deformable
objects can
change their
shape over
time, e.g. lips,
hands.
Figure from Kass et al. 1987

44. Why do we want to fit deformable
shapes?
• Some objects have similar basic form but
some variety in the contour shape.
Slides by Kristen Grauman, UT-Austin

45. Deformable contours: intuition
Image from http://www.healthline.com/blogs/exercise_fitness/uploaded_images/HandBand2-795868.JPG Figure from Shapiro & Stockman

46. Deformable contours
initial intermediate final
a.k.a. active contours, snakes
How is the current contour adjusted to find the new contour at
each iteration?
• Define a cost function (“energy” function) that says how
good a possible configuration is.
• Seek next configuration that minimizes that cost function.
What are examples of problems with energy functions
that we have seen previously?

47. Snakes energy function
The total energy (cost) of the current snake is
defined as:
externalinternaltotal EEE 
A good fit between the current deformable contour
and the target shape in the image will yield a low
value for this cost function.
Internal energy: encourage prior shape preferences:
e.g., smoothness, elasticity, particular known shape.
External energy (“image” energy): encourage contour to
fit on places where image structures exist, e.g., edges.

48. 10))(),(()(  ssysxs
Parametric curve representation
(continuous case)
Fig from Y. Boykov

49. External energy: intuition
• Measure how well the curve matches the image data
• “Attract” the curve toward different image features
– Edges, lines, etc.

50. External image energy
Magnitude of gradient
- (Magnitude of gradient)
 22
)()( IGIG yx 
22
)()( IGIG yx 
How do edges affect
“snap” of rubber
band?
Think of external
energy from image
as gravitational pull
towards areas of
high contrast

51. External image energy
• Image I(x,y)
• Gradient images and
• External energy at a point v(s) on the curve is
• External energy for the whole curve:
),( yxGx ),( yxGy
)|))((||))((|())(( 22
sGsGsE yxexternal  

1
0
))(( dssEE externalexternal 

52. Internal energy: intuition

53. Internal energy: intuition
http://www3.imperial.ac.uk/pls/portallive/docs/1/52679.JPG
A priori, we want to favor smooth shapes,
contours with low curvature, contours
similar to a known shape, etc. to balance
what is actually observed (i.e., in the
gradient image).

54. Internal energy
For a continuous curve, a common internal energy term is the “bending energy”.
At some point v(s) on the curve, this is:
The more the curve
bends  the larger
this energy value is.
The weights α and β
dictate how much
influence each
component has.
Elasticity,
Tension
Stiffness,
Curvature
sd
d
ds
d
sEinternal
2
2
))((
22
  

1
0
))(( dssEE internalinternal 
Internal energy
for whole curve:

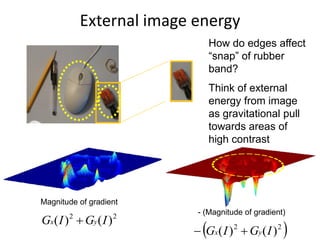
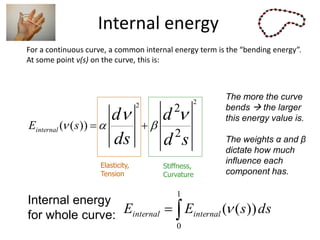
55. Dealing with missing data
• The smoothness constraint can deal with missing data:
[Figure from Kass et al. 1987]

56. Total energy
(continuous form)
// bending energy
// total edge strength
under curve
externalinternaltotal EEE 

1
0
internal ))(( dssEEinternal 

1
0
))(( dssEE externalexternal 

57. Parametric curve representation
(discrete form)
• Represent the curve with a set of n points
10),(  niyx iii  …

58. Discrete energy function:
external term
2
1
0
2
|),(||),(| iiy
n
i
iixexternal yxGyxGE 



Discrete image gradients
),( yxGx ),( yxGy
• If the curve is represented by n points

59. Discrete energy function:
internal term
• If the curve is represented by n points
Elasticity,
Tension
Stiffness
Curvature
10),(  niyx iii 
i1iv
ds
d


  11112
2
2)()(   iiiiiii
ds
d





 
1
0
2
11
2
1 2
n
i
iiiiiinternalE 
…

60. Penalizing elasticity
• Current elastic energy definition uses a discrete estimate of
the derivative, and can be re-written as:
Possible problem with this
definition?
This encourages a closed
curve to shrink to a cluster.




1
0
2
n
i
iinternal LE  2
1
1
0
2
1 )()( ii
n
i
ii yyxx  




61.  
21
0
2
1
2
1 )()(


 
n
i
iiiiinternal dyyxxE 
Penalizing elasticity
• To stop the curve from shrinking to a cluster of points, we can
adjust the energy function to be:
• This encourages chains of equally spaced points.
Average distance between pairs of points –
updated at each iteration

62. Function of the weights

large  small medium 
• weight controls the penalty for internal elasticity




1
0
2
n
i
iinternal LE  2
1
1
0
2
1 )()( ii
n
i
ii yyxx  



Fig from Y. Boykov

63. Optional: specify shape prior
• If object is some smooth variation on a known
shape, we can use a term that will penalize
deviation from that shape:
where are the points of the known
shape.




1
0
2
)ˆ(
n
i
iiinternalE 
}ˆ{ i
Fig from Y. Boykov

64. Summary: elastic snake
• A simple elastic snake is defined by
– A set of n points,
– An internal elastic energy term
– An external edge based energy term
• To use this to locate the outline of an
object
– Initialize in the vicinity of the object
– Modify the points to minimize the total
energy
How should the weights in the energy function be chosen?

65. Energy minimization
• Several algorithms proposed to fit deformable
contours, including methods based on
– Greedy search
– Dynamic programming (for 2d snakes)
– (Gradient descent)

66. Energy minimization: greedy
• For each point, search window around it
and move to where energy function is
minimal
– Typical window size, e.g., 5 x 5 pixels
• Stop when predefined number of points
have not changed in last iteration, or after
max number of iterations
• Note
– Convergence not guaranteed
– Need decent initialization

67. Values shown in the cells correspond to Etotal
3/19/2020 67
Tiilikainen NP. A Comparative Study of Contour Snakes. 2007.

68. 3/19/2020 68
Snakes: Parameters

69. 3/19/2020 69

70. 3/19/2020 70

71. 3/19/2020 71
Assignment 2: Edge and boundary detection (Hough transform and SNAKE)
Due time: March 16th, 2020, 11:59 pm
For given images (grayscale and color)/you may run on other images
A) Tasks to implement
For all given images; detect edges using Canny edge detector, detect lines, circles,
ellipsed located in these images (if any). Superimpose the detected shapes on the
images.
For given images; initialize the contour for a given object and evolve the Active
Contour Model (snake) using the greedy algorithm. Represent the output as chain
code and compute the perimeter and the area inside these contours.
B) Report all of the above to TA’s (One Zip file including report, codes, results, etc).