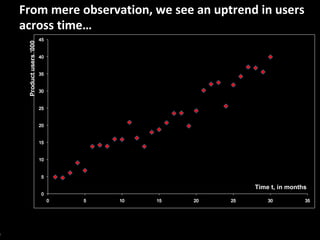
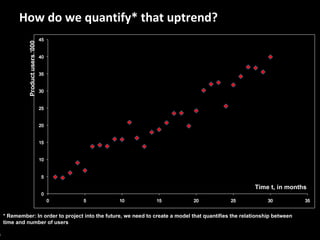
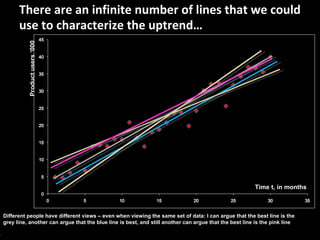
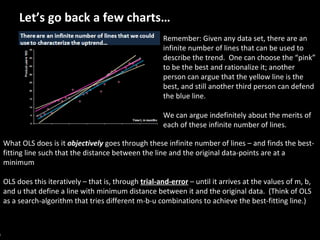
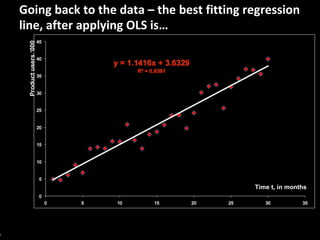
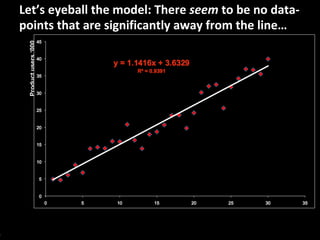
This document serves as a non-technical introduction to econometrics, focusing on linear regression and its application in understanding relationships between predicted and predictor variables. It aims to make econometric concepts accessible to readers with no prior knowledge, emphasizing the importance of a curious mindset and basic arithmetic skills. Additionally, it discusses the use of Ordinary Least Squares (OLS) in deriving a regression line that minimizes distance from actual data points, providing a framework for estimating future trends based on historical data.

1. What is econometrics? Simple, non-technical introduction on Linear Regression/OLS as a technique

2. About this document… This document is not meant for presentation and is best viewed together in slideshow or printed format. It is meant to be ‘read’, not ‘presented’ This document also covers the very basics of Econometrics. Econometrics – as a subject – is theoretically complex. The goal of this document is to empower the reader with an understanding of econometrics so she/he can discuss the topic with some confidence

3. About this document This document assumes ‘zero-knowledge’ in econometrics and in linear regression It may appear to be long-winded at times, but it is designed to be so in order impress upon the reader the concepts that are being discussed herein Some online references and books are at the end of the document for those who are interested in further learning about econometric and statistical modeling

4. About this document Readers who have either a formal background in, conceptual understanding of, or keen interest in statistics would find this document helpful in ‘transitioning’ towards econometric modeling… A conceptual understanding of linear regression will also be helpful to appreciate econometrics, but this document will assume zero-knowledge in regression Econometrics as a science is founded on complex equations and assumptions based on the theories of probability and statistics – these are not covered in this document.

5. What is econometrics?

6. “Econometrics? Isn’t that difficult?”

7. It’s full of formulas… and it could be complex

8. But…

9. Things must be made as simple as possible – but never simpler

10. This is an attempt to present econometrics as simple as possible…

11. What’s required to learn a little bit of econometrics

12. … lots of curiosity

13. … a little bit of patience

14. … a little bit of brains

15. … confidence in dealing with numbers

16. … a belief that numbers can tell stories

17. Let’s start with a little bit of definition What is econometrics?

18. What is econometrics? Econometrics is an application of statistics and mathematics … aimed at identifying and quantifying the relationships between two sets of variables – (1) the predicted variables and (2) the predictor variables. The goal of econometrics is to test a hypothesized causal relationship between the predicted and the predictor variables.

19. What is econometrics? Econometrics is an application of statistics and mathematics Econometrics is derived from statistics – largely regression and ‘trending’ techniques - and from mathematics There are differences between statistics and econometrics – but the differences are academic*… * … but not necessarily moot and unimportant For those interested about the differences, see future tutorials…

20. What is econometrics? … aimed at identifying and quantifying the relationships between two sets of variables – (1) the predicted variables and (2) the predictor variables. The basic goal of econometrics is to explain using formulas and numbers the relationship between a predictor variable – such as GRPs, adspends, competitive spends, temperature, and seasonality – and a predicted variable – such as awareness, sales, revenues, and profits

21. What is econometrics? This relationship is expressed in an equation – such as y is the ‘predicted’ variable x is the ‘predictor’ variable m , b and u are the values that econometrics want to uncover

22. What is econometrics? This relationship is expressed in an equation – such as y is the ‘predicted’ variable x is the ‘predictor’ variable m , b and u are the values that econometrics want to uncover We know the values of y and x Econometrics helps us identify the values of m, b and u

23. If we were interested in awareness and GRPs… We can rewrite the first equation taking our interest into consideration as follows awareness = m • GRPs + b + u NB. This is simplifying the relationship between GRPs and awareness drastically. The relationship is far more complex, of course – but let’s assume that this equation is true for now. What econometrics does is “estimate” the values of “m”, “b” and “u” based on the available data on Awareness and GRPs, such that we have an equation that relates Awareness and GRPs. Once m, b and u are identified and estimated, we can then use the equation to explain the movements in awareness with respect to GRPs – and predict how awareness is going to move in the future given different levels of GRPs

24. There are many econometric techniques… But the most common technique is linear regression

25. What is linear regression ? A brief introduction to linear regression How to create regression lines? Regression in econometrics and marketing

26. Introduction to linear regression Let’s assume that x is the evolution of the number of users of a certain product across months (in ‘000), represented by time t In the first month, for example, we see that there are 4’905 users of the product. By the 5 th month, that has increased to about 6’800 users – and by the 26 th month, the number of users have increased to around 34’200 Clearly, there is an increase in the number of users – and it seems, from looking at the data alone that indeed, there is a significant uptrend

27. If we plotted the data, we would indeed see an upward trend… Time t, in months Product users ‘000 In the 1 st month, we see that there are about 5’000 product users By the 30 th month, the number of users have increased to about 40’000 users

28. The question If this trend held and continued into the next 12 months, how many more users will we have?

29. To answer this question… … we need to understand first the past relationship between the two variables – time and numbers of users . We will then use this understanding of the past to predict what’s going to happen in the next 12 months The Past The Future

30. What bridges the gap between the past and the future… Once we have identified the equation or the model, we will have a better grasp of (1) the past trends and (2) the potentials of the future Linear regression comes into the picture by bridging that gap between the past and the future The Past The Future Linear regression equation

31. With that in mind, let’s look at the chart again

32. From mere observation, we see an uptrend in users across time… Time t, in months Product users ‘000

33. How do we quantify* that uptrend? Time t, in months Product users ‘000 * Remember: In order to project into the future, we need to create a model that quantifies the relationship between time and number of users

34. There are an infinite number of lines that we could use to characterize the uptrend… Time t, in months Product users ‘000 Different people have different views – even when viewing the same set of data: I can argue that the best line is the grey line, another can argue that the blue line is best, and still another can argue that the best line is the pink line

35. Linear regression insists that there is one (and only one) line that would best characterize the trend and the relationship between the two variables

36. Linear regression also insists that this equation be of the following form: … where y is the number of users per month ‘000 x is time b is the constant u is the unexplained variance

37. This one line that best describes the relationship between the two variables is derived through OLS OLS – which stands for “ordinary least squares” – is an algorithm that defines the values of m , b and u … such that the distance between the actual values and the line defined by the final values of m, b and u are at its minimum Huh

38. Let’s go back a few charts… What OLS does is it objectively goes through these infinite number of lines – and finds the best-fitting line such that the distance between the line and the original data-points are at a minimum OLS does this iteratively – that is, through trial-and-error – until it arrives at the values of m, b, and u that define a line with minimum distance between it and the original data. (Think of OLS as a search-algorithm that tries different m-b-u combinations to achieve the best-fitting line.) Remember: Given any data set, there are an infinite number of lines that can be used to describe the trend. One can choose the “pink” to be the best and rationalize it; another person can argue that the yellow line is the best, and still another third person can defend the blue line. We can argue indefinitely about the merits of each of these infinite number of lines.

39. Going back to the data – the best fitting regression line, after applying OLS is… Time t, in months Product users ‘000

40. By applying OLS, the equation «y = 1.416x + 3.6329» is found to be the best-fitting regression line It is objective and unbiased By using OLS, we are assured that this is unbiased and objective It is linear It conforms to the «y= mx + b + u» requirement of econometrics) It is the best-fitting line Because the OLS algorithm is aimed at minimizing the distance between the line and the data points, we are assured that it is the best-fitting line

41. Now comes the interesting part… So what does the equation exactly mean?

42. The story behind «y = 1.416x + 3.6329» This equation suggests the following – For every 1.416-unit change in x , there is a corresponding 1-unit change in y Applying this to our data, we can say that for every 1.416 months (about 5-6 weeks), there is an additional 1’000 new users of the product 3.6329 is called the constant – it is the number of users when the product was rolled out into the marketplace (at time t = 0) These are perhaps the early adopters of the product or those who have been exposed to the product through free samples

43. OK, we have an equation – how do we know it’s the correct equation? First, we “eyeball” the line and the actual data Are the data points within ‘reasonable’ distance of the line? If each of the data points seem to be near the trendline, then we can say initially that we have a good fit If there are data-points that are significantly far from the line, then the equation may need to be revisited – or that outlying data-point may be caused by something else apart from time

44. Let’s eyeball the model: There seem to be no data-points that are significantly away from the line… Time t, in months Product users ‘000

45. Eyeballing the data, however, brings back subjective interpretations Time t, in months Product users ‘000 One can argue that point at month 11 is significantly away from the line – and so is data for month 24… We therefore need a more accurate, more objective measurement of “fit”

46. How else do we know if the equation is valid or not? We look at the r-squared (r 2 ) – 0.9391 This suggests that the variable “time” is able to explain 93.91% of the variance or movements in the number of users The other 6.09% are unexplained by the variable “time” – and could be due to other factors that are beyond time The 6.09% unexplained variance could also be because of errors in measurements, or simply ‘random’ errors that we will never be able to uncover An r-squared of 0.75+ is considered to be acceptable as a ‘rule-of-thumb’ The r-squared is only one of few that measure goodness-of-fit (GIF). Other measures include adjusted R-squared, AIC/Akaike Information Criteria, RMSE/root-mean squared error, and GLM-ANOVA. These will not be discussed here.

47. Will we ever have a r-squared of 1.00? Possible – but highly improbable The higher the r-squared, the better – and it possible to have a 1.00 r-squared, but in the real world, highly-improbable A r-squared of 1.00 will only happen in a perfect scenario where the model perfectly fits and explains the data Getting an r-squared of 0.75+ in and of itself will be a challenge

48. But there are deviations between the line and the data! Why do we have deviations? Because there are other things that we probably are not taking into account in this model

49. Deviations are not entirely bad… Actually, the deviations are part of the story… Because these deviations are an indication that something else apart from time is at work, it is worth checking why these deviations exist This is where analytics and econometrics/statistics meet – uncovering why things are explainable and not-explainable by a model .

50. Let’s go back to the original question:

51. What have we done so far…? We’ve modeled and derived an equation relating time-t with purchases for the first 30months

52. What have we done so far…? We’re fairly confident with the model because it explains about 94% of the variance in the number of purchasers, as reflected by the r-squared

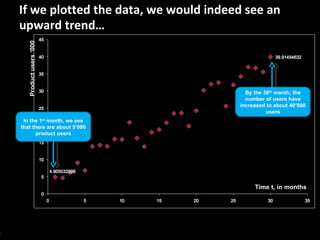
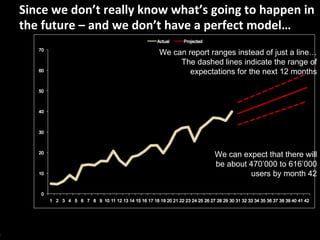
53. Let’s now project what’s going to happen in the next 12 months… Time t, in months Product users ‘000 At the end of the next 12 months [by month 42], we can expect to have 543’000 users – if all things remain equal

54. Since we don’t really know what’s going to happen in the future – and we don’t have a perfect model… We can report ranges instead of just a line… The dashed lines indicate the range of expectations for the next 12 months We can expect that there will be about 470’000 to 616’000 users by month 42

55. Are you still there?

56. Take a sigh of relief…

57. Linear regression through OLS is just amongst of the many techniques in econometrics… For those interested… Wikipedia’s page on linear regression is here and the OLS technique is discussed here . Specifically on econometrics, Wikipedia’s entry is here . An international organization of econometricians – and some information on econometrics – can be found here . A more detailed introduction to econometrics can be found here .

58. Books on econometrics that we’ve found useful… Econometrics by Samuel Cameron, in Amazon.Com , is an approachable introduction to the concepts Introductory Econometrics by Humberto Barreto uses Microsoft Excel® and includes a CD-ROM with interactive files. A Guide to Econometrics by Peter Kennedy is considered by most teachers in beginning econometrics and practitioners to be a good guide

59. Other books that might be helpful Probability plays a major role in econometrics; for those interested, ET Jaynes has an e-book (in PDF) here . This is heavy reading, but enlightening. An HTML version can be found here Since econometrics builds on statistical theory, try reading chapters on linear regression (bivariate/multivariate) in Stat101 books. Amazon has this list for you to choose from.

60. Credits for the images use Most of the images in the presentation are from Gettyimages.Com; the ownership of GettyImages over these photos are asserted and no claims are made by the presenter, author, nor by the company on these images. We acknowledge GettyImages’ ownership of copyright over their work in this presentation. We also acknowledge and claim no ownership of the other images that have been used in this presentation/file.

61. This presentation Author: Philip Tiongson [email_address] Audiences: Staff interested in the basics of econometrics