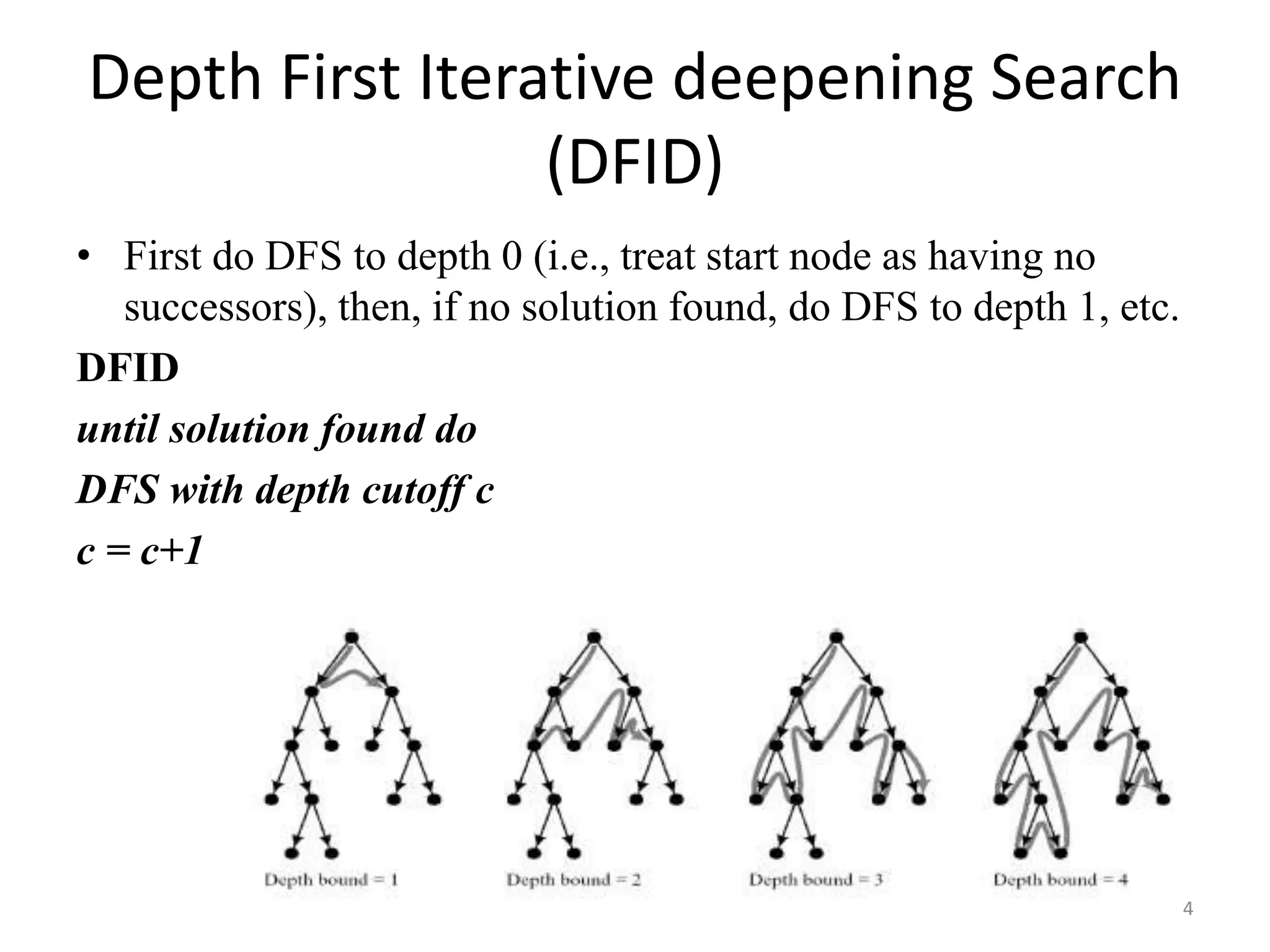
Depth-limited search is a variation of depth-first search that limits the depth of node exploration to circumvent problems with unbounded depth-first search. Branch and bound search uses heuristics to prune parts of the search tree that cannot possibly contain better solutions than what has already been found. Depth-first iterative deepening search exhaustively searches each level of the search tree, starting from depth 0 and incrementally increasing the depth, until a solution is found. Bidirectional search simultaneously explores the search space from the start and goal nodes until their frontiers intersect, potentially finding solutions faster than unidirectional search.

1. Uninformed Search
Lecture-10
Hema Kashyap
1

2. Depth Limited Search
• A variation of Depth First Search circumvents the above problem by keeping a
depth bound.
• Nodes are only expanded if they have depth less than the bound. This algorithm
is known as depth-limite d search.
2

3. Branch and Bound
1. Initialize: set OPEN=s, CLOSED={}, c(s)=0, c*=∞
2. Fail: If OPEN={}, then return C*
3. Select: Select a state n from OPEN and save in CLOSED
4. Terminate: If n∈G and C(n)<C*, then
Set C*= = C(n) and GOTO step 2
1. Expand: Check if C(n)<C* generate the successor of n
For each successor, m, insert m in OPEN only if
if m∈[OPEN∪CLOSED]
set c(m)= C[n]+C[n,m] and insert m in n
if m∈[OPEN∪CLOSED]
set c(m)= min{C[m], C[n]+C[n,m]}
If C[m]has decreased and m ∈ CLOSED move it to OPEN
2. Loop: Goto step 2
3

4. Depth First Iterative deepening Search
(DFID)
• First do DFS to depth 0 (i.e., treat start node as having no
successors), then, if no solution found, do DFS to depth 1, etc.
DFID
until solution found do
DFS with depth cutoff c
c = c+1
4

5. Properties of DFID
The algorithm is
• Complete
• Optimal/Admissible if all operators have the same cost. Otherwise, not
optimal but guarantees finding solution of shortest length (like BFS).
• Time complexity is a little worse than BFS or DFS because nodes near the
top of the search tree are generated multiple times, but because almost all of
the nodes are near the bottom of a tree, the worst case time complexity is still
exponential, O(bd)
If branching factor is b and solution is at depth d, then nodes at depth d are
generated once, nodes at depth d-1 are generated twice, etc.
Hence bd + 2b(d-1) + ... + db <= bd / (1 - 1/b)2 = O(bd).
• Linear space complexity, O(bd), like DFS
This algorithm is generally preferred for large state spaces where the solution
depth is unknown.
5

6. Bidirectional Search
• Bidirectional search involves alternate
searching from the start state toward the
goal and from the goal state toward the
start. The algorithm stops when the
frontiers intersect.
• A search algorithm has to be selected for
each half.
• Bidirectional search can sometimes lead
to finding a solution more quickly. The
reason can be seen from inspecting the
following figure
6

7. Comparing Uninformed Search
Strategy
7