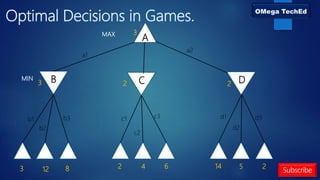
This document discusses adversarial search and the minimax algorithm. It defines adversarial search as games where two or more players with conflicting goals explore the same search space for a solution. It describes the components of a game problem including the initial state, players, actions, results, terminal test, and utility function. It introduces the game tree that represents the game as a tree with states as nodes and moves as edges. It then explains the minimax algorithm, which uses recursion to determine the optimal strategy by finding the minimum of the maximum values for MAX and the maximum of the minimum values for MIN through the game tree.

1. 16
ADVERSARIAL SEARCH
GAMES & MINIMAX ALGORITHM

2.  The term “search” in the context of adversarial
search refers to games.
Subscribe
Adversarial Search
“Searches in which two or more players with
conflicting goals are trying to explore the same
search space for the solution, are called
adversarial searches, often known as Games”.

3. Problem Formulation
 INITIAL STATE: It specifies how the game is set up at the start.
 PLAYER(s): It specifies which player has moved in the state
space.
 ACTION(s): It returns the set of legal moves in state space.
 RESULT(s, a): It is the transition model, which specifies the
result of moves in the state space.
 TERMINAL-TEST(s): Terminal test is true if the game is over,
else it is false at any case. The state where the game ends is
called terminal states.
 UTILITY(s, p): A utility function gives the final numeric value for a
game that ends in terminal states s for player p. It is also called
payoff function. For Chess, the outcomes are a win, loss, or draw
and its payoff values are +1, 0, ½. And for tic-tac-toe, utility
values are +1, -1, and 0.
Subscribe

4. Game Tree
Subscribe
The initial state, ACTIONS
function, and RESULT
function define the game
tree for the game.
In game tree nodes are
game states and the edges
are moves.

5. Subscribe
Optimal Decisions in Games.
A
B D
C
MAX
MIN
3 8
12 6
4
2 14 5 2
3 2 2
3
a1
a2
b1
b2
b3 c1
c2
c3 d1
d2
d3

6. Minimax Algorithm
Subscribe
The optimal strategy can be determined from the minimax value of each
node, which we write as MINIMAX(n). MAX prefers to move to a state of
maximum value, whereas MIN prefers a state of minimum value. So we have
the following:
MINIMAX(s)=
UTILITY(s) if TERMINAL-TEST(s)
max Єactions(s) MINIMAX(RESULT(s,a)) if PLAYER(s)=MAX
min Єactions(s) MINIMAX(RESULT(s,a)) if PLAYER(s)=MIN

7. Subscribe
Example
A
D F G
B C
MAX
MIN
-1 5
2
-2
-3
3
a1 a2
b1 b2
c1 c2
2
MAX
1
2 5
2
2
3 -2
-2
E
Time Complexity O(bd )
b= Branching factor
d= depth (ply)

8. Thanks For
Watching
Reference:
Artificial Intelligence
A Modern Approach Third Edition
Peter Norvig and Stuart J. Russell
Subscribe
Like
Share
Next Topic: ALPHA-BETA PRUNING

9. OMega TechEd
About the Channel
This channel helps you to prepare for BSc IT and BSc computer science subjects.
In this channel we will learn Business Intelligence ,Artificial Intelligence, Digital Electronics,
Internet OF Things Python programming , Data-Structure etc.
Which is useful for upcoming university exams.
Gmail: omega.teched@gmail.com
Social Media Handles:
omega.teched
megha_with
Subscribe