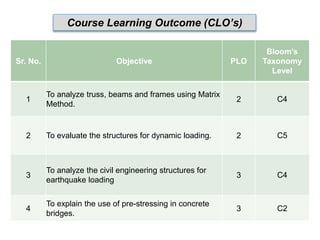
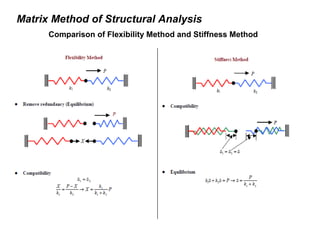
The document outlines the course structure for CE-412: Structural Engineering, detailing instructors, class rules, key topics, and assessment methods. It covers matrix methods of analysis, classical vs matrix methods, finite element method applications, and the principles of structural analysis, emphasizing the importance of understanding both stiffness and flexibility. Additionally, it includes course learning outcomes aligned with Bloom's taxonomy and references essential textbooks for further reading.

1. CE-412: STRUCTURAL ENGINEERING

2. Teachers/Instructors:
1.Prof. Dr. Asif Hameed
2.Prof. Dr. Burhan Sharif
3.Dr. Ali Ahmed
Class Rules:
1. Attendance: You are expected in each class, Attendance less
than 75% will attribute to the WF grade.
2. Participation: Class participation and discussion will be
encouraged and have 5% marks.
3. Cell phone: Preferably don’t bring in the class.
However, the use of mobile phone during lecture are strictly not
allowed.
4. You are expected to produce your own work
5. Assignments should be submitted in proper folder.
CE-412: STRUCTURAL ENGINEERING

3. 3
CE-412: STRUCTURAL ENGINEERING
Matrix methods of analysis:
Virtual force principle and flexibility method, flexibility of bar, beam
and general flexural elements, analysis of 2D framed structures
with temperature, support settlement and lack of fit, Virtual
displacement principle and displacement method. Element
stiffness matrix for bar, beam and plane frame element, coordinate
transformation Compatibility and equilibrium. Assembly of
structure stiffness matrix Analysis by stiffness method of 2D
trusses, beams and frames including temperature effects, lack of
fit and settlement of supports. Reliability of computer results
Computer applications of above using interactive computer
programs. Analysis by stiffness method of 2D-Reliability of
computer results.
CHAPTER OUTLINE

4. 4
CE-412: STRUCTURAL ENGINEERING
CHAPTER OUTLINE
Introduction to Structural Dynamics and Earthquake Engineering:
Vibration of SDOF lumped mass systems, free and forced vibration with and
without viscous damping ,Natural vibration of SDOF systems , Response of
SDOF systems: to harmonic excitation, to specific forms of excitation of ideal
step, rectangular, pulse and ramp forces, Unit impulse response Vibration of
MDOF systems with lumped mass Hamilton’s principle, modal frequency and
mode shapes ,Computer applications of above Introduction to basic
terminology in EQ engineering ,Form of structures for EQ resistance, Ductility
demand, damping etc ,Seismic zoning of Pakistan ,Equivalent lateral force
analysis ,Detailing of RC structures for EQ resistance.
Prestressed Concrete: Principles, techniques and types, tendon profiles etc
Losses of prestress, Analysis of Prestressed concrete for service load, cracking
load and ultimate strength Design and detailing of simply support post-and pre-
tensioned beams.
Bridge Engineering: Site selection for a bridge, types and structural forms of
bridges, Construction methods Vehicle load transfer to slab and stringers
Design and detailing of simple RC deck and girder bridges.

5. Matrix Method of Structural Analysis
Reference Books
1. Matrix Analysis of Structures by Aslam Kassimali, Second Edition
2. A First Course in the Finite Element Method Daryl L. Logan,
Fourth Edition
3. Structural Analysis by R. C Hibbeler Eighth Edition.
4. Analysis of Structures, Stiffness Methods by Dr. Saeed Ahmad.
5. The Finite Element Method using MATLAB By Kwon and Bang.

6. Course Learning Outcome (CLO’s)
Sr. No. Objective PLO
Bloom’s
Taxonomy
Level
1
To analyze truss, beams and frames using Matrix
Method.
2 C4
2 To evaluate the structures for dynamic loading. 2 C5
3
To analyze the civil engineering structures for
earthquake loading
3 C4
4
To explain the use of pre-stressing in concrete
bridges.
3 C2

7. • Structural analysis, which is an integral part of any structural
engineering project, is the process of predicting the
performance of a given structure under a prescribed loading
condition.
• The performance characteristics usually of interest in
structural design are: (a) stresses or stress resultants (i.e.,
axial forces, shears, and bending moments); (b) deflections;
and (c) support reactions.
• Thus, the analysis of a structure typically involves the
determination of these quantities as caused by the given
loads and/or other external effects (such as support
displacements and temperature changes).
Structural Analysis

8. • The classical methods of structural analysis (also known as system
approach of analysis), such as the method of consistent
deformation, slope-deflection methods, moment distribution etc.,
consider the behavior of the entire structure for developing
equations necessary for analysis. Hence, these methods are
suitable only for simple or small structures.
• Benefits of studying classical Methods of Analysis are:
a. Understanding the behavior of the structure.
b. Understanding the principles of Structural Analysis.
c. Developing the basic equations of Analysis.
d. In preliminary analysis/design and quick checking of the
analysis results.
e. Analysis of small structures
Classical Methods of Structural Analysis

9. • For larger structures, the use of classical methods of analysis will be
difficult and time-consuming. Even though the procedures using
classical methods can be written in matrix format, the Matrix
methods of structural analysis is different from the classical
approach and is known as the element approach of analysis.
• In this method, the response of the whole structure is determined
using the behavior of the elements or members from which the
structure is made of.
• In most design offices today, the analysis of framed structures is
routinely performed on computers, using software based on the
matrix methods of structural analysis. It is therefore essential that
structural engineers understand the basic principles of matrix
analysis, so that they can develop their own computer programs
and/or properly use commercially available software—and
appreciate the physical significance of the analytical results.
Matrix Structural Analysis

10. Matrix Structural Analysis
Historical Background
• The foundation of matrix method was laid by James C Maxwell in 1864
who also invented method of consistent deformation.
• Later, many researchers contributed towards the present available
matrix method, the prominent among them are S.S. Archer, C.K. Wang,
H.C. Martin, E. L. Wilson.
• In the pre-computer era, the main disadvantage of the matrix methods
was that they required direct solution of simultaneous algebraic
equations—a formidable task by hand calculations in cases of more
than a few unknowns.
• The invention of computers in the late 1940s revolutionized structural
analysis. As computers could solve large systems of simultaneous
equations.
• Since the mid-1950s, the development of matrix methods has continued
at a tremendous pace, with research efforts in recent years directed
mainly toward formulating procedures for developing efficient
computational techniques for analyzing large structures.

11. Classical vs Matrix Method
Classical Methods Matrix Method
 Most classical methods were
developed to analyze types of
structure and since they were intended
for hand calculations. For e.g., MDM
used only to analyze beams and plane
frames undergoing bending
deformations.
 In case of analysis of large structures,
classical methods are very tedious and
time consuming.
 A study of classical methods is
essential for developing and
understanding the structural behavior.
 Classical methods may also be used
for preliminary designs for checking
the results of computerized analysis.
• Matrix method are systematic and can
be easily programmed.
• With the use of matrix method and
computer computational power, it
becomes feasible to analyze large
structures.

12. Finite Element Method
• Matrix Method can be used to analyze skeleton structures (Plane and
Space Trusses, Beams, Plane and Space Frames and Grids etc.) only.
• Finite Element Method (FEM) which originated as an extension of matrix
analysis is used for analysis of plates and shells and now developed to
such an extent that it is applicable to all kind of Engineering Problems.
• The FEM is one of the most important developments in computational
methods to occur in the 20th century.
• FEM Is a numerical procedure for obtaining approximate solutions to many
of the problems encountered In Engineering Analysis.

13. Application of Finite Element Method
The range of applications of finite elements is too large to list, but to provide an idea of its
versatility we list the following:

14. Application of Finite Element Method
This is a very short list that is just intended to give you an idea of
the breadth of application areas for the method. New areas of
application are constantly emerging.

15. A Correct Solution of the structure satisfy the following
requirements:
Equilibrium of Forces: The external forces applied to the
structure and the internal forces induced in the members are in
equilibrium.
Compatibility of Displacements (Kinematic): Displacements
of the structure at a particular point must be compatible with
the strain within the structure at that point.
Force Displacement Relationship (Constitutive): The
internal stresses and strains satisfy the stress strain relationship
of the member.
Structural Analysis Requirements

16. Stiffness Vs Flexibility
Stiffness: Stiffness is a measure of the resistance to deformation. From
Hook’s law within the elastic range F=K.d. Here, k is the stiffness.
Flexibility: Flexibility is a measure of the ability to deform under the load.
It is the reciprocal of stiffness. f=1/k is the flexibility.

17. Matrix Method of Structural Analysis
• Strength and stiffness are not the same thing.
• Here's an analogy: A rubber band is stretched to failure.
• The rubber band failed at five pounds of force, but it stretched more than
double its length before failure. The rubber band was not very stiff. In fact, it
was elastic.
• Next, we stretch a kite string and find that it also fails at five pounds.
• It only stretched five percent before failure. It is very stiff.
• Both the rubber band and the kite string have the same ultimate strength.
However, one is very stiff and the other is very flexible.
• This should demonstrate that strength and stiffness are not the same thing,
and they are dependent upon the type of material.
• Furthermore, the shape of the material also determines its stiffness without
affecting its ultimate strength.
• For instance, if we take a plastic ruler that is 1/8" thick and 1" wide and bend
it in the flat direction it is obvious that it is flexible.
• However, if we try to bend across the 1" thickness, we find that it is very stiff.

18. Matrix Method of Structural Analysis
Two different methods can be used for the matrix analysis of structures:
the flexibility method, and the stiffness method.
The flexibility method, which is also referred to as the force or
compatibility method. In this approach, the primary unknowns are the
redundant forces, which are calculated first by solving the structure’s
compatibility equations. Once the redundant forces are known, the
displacements can be evaluated by applying the equations of equilibrium
and the appropriate member force–displacement relations.
The stiffness method, is also called the displacement or equilibrium
method. In this approach, the primary unknowns are the joint
displacements, which are determined first by solving the structure’s
equations of equilibrium. With the joint displacements known, the
unknown forces are obtained through compatibility considerations and
the member force–displacement relations.

19. Matrix Method of Structural Analysis
Comparison of Flexibility Method and Stiffness Method

20. Matrix Method of Structural Analysis
Stiffness Method Flexibility Method
1. Stiffness method uses matrices
right from the start.
2. Stiffness method has a similar
procedure both for statically
determinate and indeterminate
structures.
3. Stiffness method generates
forces and displacements
directly.
4. Stiffness method can be easily
programmed for computers.
1. This method may use matrices
but after some manual
calculations.
2. Flexibility method has a different
procedure both for statically
determinate and indeterminate
structures.
3. Additional steps are necessary
to determine displacements and
internal forces.
4. Can be programmed into a
computer, but human input is
required to select primary
structure and redundant forces.