This document provides an introduction to propositional logic and logical connectives. Some key points:
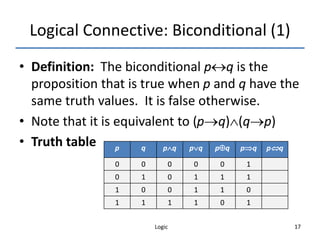
- Propositional logic deals with propositions that can be either true or false. Common logical connectives are negation, conjunction, disjunction, implication, biconditional.
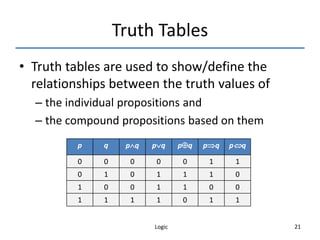
- Truth tables are used to define the semantics and truth values of logical connectives and compound propositions.
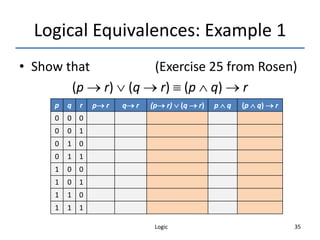
- Logical equivalences allow replacing a proposition with an equivalent proposition to simplify expressions or arguments. Equivalences can be shown using truth tables or known equivalence rules.
- Propositional logic and logical reasoning form the basis of mathematical reasoning and are useful in areas like computer science, programming, and satisfiability problems.



























![Logic 30
Logic in Programming: Example 2
• Say we have the following loop
While
((i<size AND A[i]>10) OR
(i<size AND A[i]<0) OR
(i<size AND (NOT (A[i]!=0 AND NOT (A[i]>=10)))))
• Is this a good code? Keep in mind:
– Readability
– Extraneous code is inefficient and poor style
– Complicated code is more prone to errors and difficult
to debug
– Solution? Comes later…](https://image.slidesharecdn.com/lecture01-230404162244-9bf8a94b/85/Lecture-01-ppt-30-320.jpg)








![Logic 40
Logic in Programming: Example 2
(revisited)
• Recall the loop
While
((i<size AND A[i]>10) OR
(i<size AND A[i]<0) OR
(i<size AND (NOT (A[i]!=0 AND NOT (A[i]>=10)))))
• Now, using logical equivalences, simplify it!
• Using De Morgan’s Law and Distributivity
While ((i<size) AND
((A[i]>10 OR A[i]<0) OR
(A[i]==0 OR A[i]>=10)))
• Noticing the ranges of the 4 conditions of A[i]
While ((i<size) AND (A[i]>=10 OR A[i]<=0))](https://image.slidesharecdn.com/lecture01-230404162244-9bf8a94b/85/Lecture-01-ppt-40-320.jpg)
![Logic 41
Programming Pitfall Note
• In C, C++ and Java, applying the commutative
law is not such a good idea.
• For example, consider accessing an integer
array A of size n:
if (i<n && A[i]==0) i++;
is not equivalent to
if (A[i]==0 && i<n) i++;](https://image.slidesharecdn.com/lecture01-230404162244-9bf8a94b/85/Lecture-01-ppt-41-320.jpg)