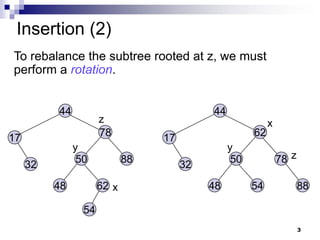
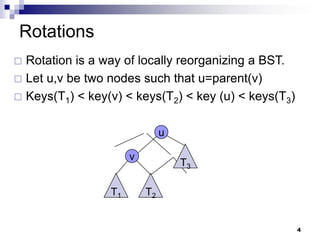
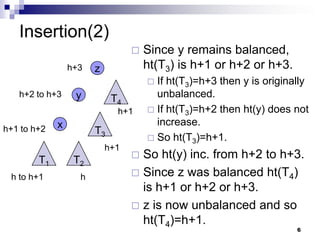
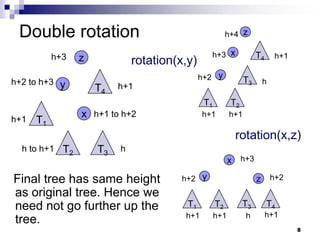
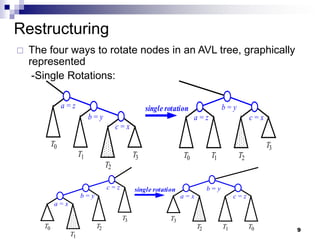
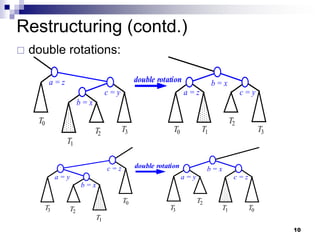
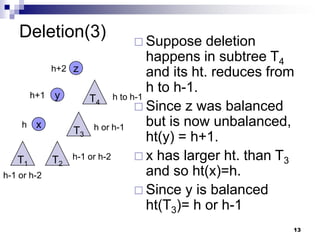
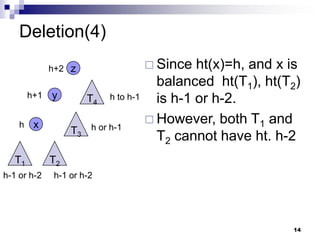
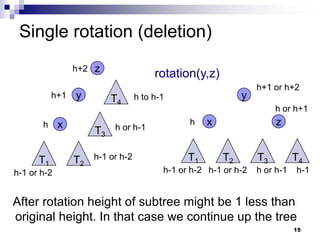
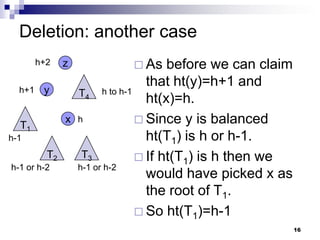
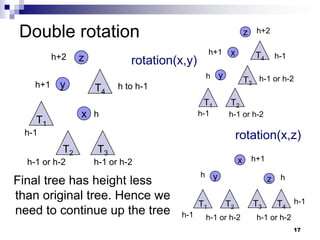
AVL trees are self-balancing binary search trees. They ensure that the height of the two subtrees of any node never differs by more than one. This balance is achieved through rotations during insertion and deletion operations. Rotations locally reorganize the tree to maintain heights differing by at most one. Both insertion and deletion in AVL trees take O(log n) time due to the potential need to traverse heights up to O(log n) during rebalancing rotations.

1. AVL Trees
 AVL Trees
1

2. Insertion
 Inserting a node, v, into an AVL tree changes the
heights of some of the nodes in T.
 The only nodes whose heights can increase are
the ancestors of node v.
 If insertion causes T to become unbalanced, then
some ancestor of v would have a height-
imbalance.
 We travel up the tree from v until we find the first
node x such that its grandparent z is unbalanced.
 Let y be the parent of node x.
2

3. Insertion (2)
To rebalance the subtree rooted at z, we must
perform a rotation.
44 44
z x
17 78 17 62
y y
50 88 50 78 z
32 32
48 62 x 48 54 88
54
3

4. Rotations
 Rotation is a way of locally reorganizing a BST.
 Let u,v be two nodes such that u=parent(v)
 Keys(T1) < key(v) < keys(T2) < key (u) < keys(T3)
u
v
T3
T1 T2
4

5. Insertion
 Insertion happens in subtree T1.
 ht(T1) increases from h to h+1. z
 Since x remains balanced ht(T2)
y T4
is h or h+1 or h+2. h+1 to h+2
 If ht(T2)=h+2 then x is originally x
unbalanced T3
 If ht(T2)=h+1 then ht(x) does not
increase. T1 T2
 Hence ht(T2)=h. h to h+1 h
 So ht(x) increases from h+1 to
h+2.
5

6. Insertion(2)
 Since y remains balanced,
h+3 z ht(T3) is h+1 or h+2 or h+3.
 If ht(T3)=h+3 then y is originally
h+2 to h+3 y T4 unbalanced.
h+1  If ht(T3)=h+2 then ht(y) does not
x increase.
h+1 to h+2 T3
 So ht(T3)=h+1.
h+1
T1 T2  So ht(y) inc. from h+2 to h+3.
h to h+1 h  Since z was balanced ht(T4)
is h+1 or h+2 or h+3.
 z is now unbalanced and so
ht(T4)=h+1.
6

7. Single rotation
h+3 z
rotation(y,z)
h+2 to h+3 y h+1 h+3 y
T4
x h+2 x z h+2
h+1 to h+2 T3
h+1
T1 T2 T1 T2 T3 T4
h+1 h h+1 h+1
h to h+1 h
The height of the subtree remains the same after
rotation. Hence no further rotations required
7

8. Double rotation h+4 z
h+3 z h+3 x T4 h+1
rotation(x,y)
h+2 y T3
h+2 to h+3 y h
T4 h+1
T1 T2
x h+1 to h+2 h+1 h+1
h+1 T1
rotation(x,z)
h to h+1 T2 T3 h
x h+3
Final tree has same height h+2 y z h+2
as original tree. Hence we
need not go further up the T1 T2 T3 T4
h+1 h+1 h h+1
tree.
8

9. Restructuring
 The four ways to rotate nodes in an AVL tree, graphically
represented
-Single Rotations:
a=z single rotation b=y
b=y a=z c=x
c=x
T0 T3
T1 T3 T0 T1 T2
T2
c=z single rotation b=y
b=y a=x c=z
a=x
T3 T3
T0 T2 T2 T1 T0 9
T1

10. Restructuring (contd.)
 double rotations:
a=z double rotation b=x
c=y a=z c=y
b=x
T0 T2
T2 T3 T0 T1 T3
T1
c=z double rotation b=x
a=y a=y c=z
b=x
T0 T2
T3 T2 T3 T1 T0
T1
10

11. Deletion
 When deleting a node in a BST, we either
delete a leaf or a node with only one child.
 In an AVL tree if a node has only one child
then that child is a leaf.
 Hence in an AVL tree we either delete a
leaf or the parent of a leaf.
 Hence deletion can be assumed to be at a
leaf.
11

12. Deletion(2)
 Let w be the node deleted.
 Let z be the first unbalanced node encountered
while travelling up the tree from w. Also, let y be the
child of z with larger height, and let x be the child of
y with larger height.
 We perform rotations to restore balance at the
subtree rooted at z.
 As this restructuring may upset the balance of
another node higher in the tree, we must continue
checking for balance until the root of T is reached
12

13. Deletion(3)  Suppose deletion
happens in subtree T4
h+2 z and its ht. reduces from
h+1 y
h to h-1.
T4 h to h-1
 Since z was balanced
h x h or h-1 but is now unbalanced,
T3
ht(y) = h+1.
T1 T2 h-1 or h-2  x has larger ht. than T3
h-1 or h-2 and so ht(x)=h.
 Since y is balanced
ht(T3)= h or h-1
13

14. Deletion(4)
h+2 z  Since ht(x)=h, and x is
balanced ht(T1), ht(T2)
h+1 y T4 h to h-1 is h-1 or h-2.
h x  However, both T1 and
T3 h or h-1
T2 cannot have ht. h-2
T1 T2
h-1 or h-2 h-1 or h-2
14

15. Single rotation (deletion)
h+2 z
rotation(y,z)
h+1 or h+2
h+1 y T4 h to h-1 y
h or h+1
h x h or h-1
h x z
T3
T1 T2 h-1 or h-2 T1 T2 T3 T4
h-1 or h-2 h-1 or h-2 h-1 or h-2 h or h-1 h-1
After rotation height of subtree might be 1 less than
original height. In that case we continue up the tree
15

16. Deletion: another case
h+2 z  As before we can claim
that ht(y)=h+1 and
h+1 y T4 h to h-1
ht(x)=h.
T1
x h  Since y is balanced
h-1 ht(T1) is h or h-1.
T2 T3  If ht(T1) is h then we
h-1 or h-2 h-1 or h-2
would have picked x as
the root of T1.
 So ht(T1)=h-1
16

17. Double rotation z h+2
h+1 x T4 h-1
h+2 z rotation(x,y)
h y
T3 h-1 or h-2
h+1 y T4 h to h-1
T1 T2
x h h-1 h-1 or h-2
T1
h-1 rotation(x,z)
T2 T3
h-1 or h-2 h-1 or h-2 x h+1
h y h
Final tree has height less z
than original tree. Hence we
T1 T2 T3 T4 h-1
need to continue up the tree h-1 h-1 or h-2 h-1 or h-2
17

18. Running time of insertion & deletion
 Insertion
 We perform rotation only once but might have to
go O(log n) levels to find the unbalanced node.
 So time for insertion is O(log n)
 Deletion
 We need O(log n) time to delete a node.
 Rebalancing also requires O(log n) time.
 More than one rotation may have to be
performed.
18