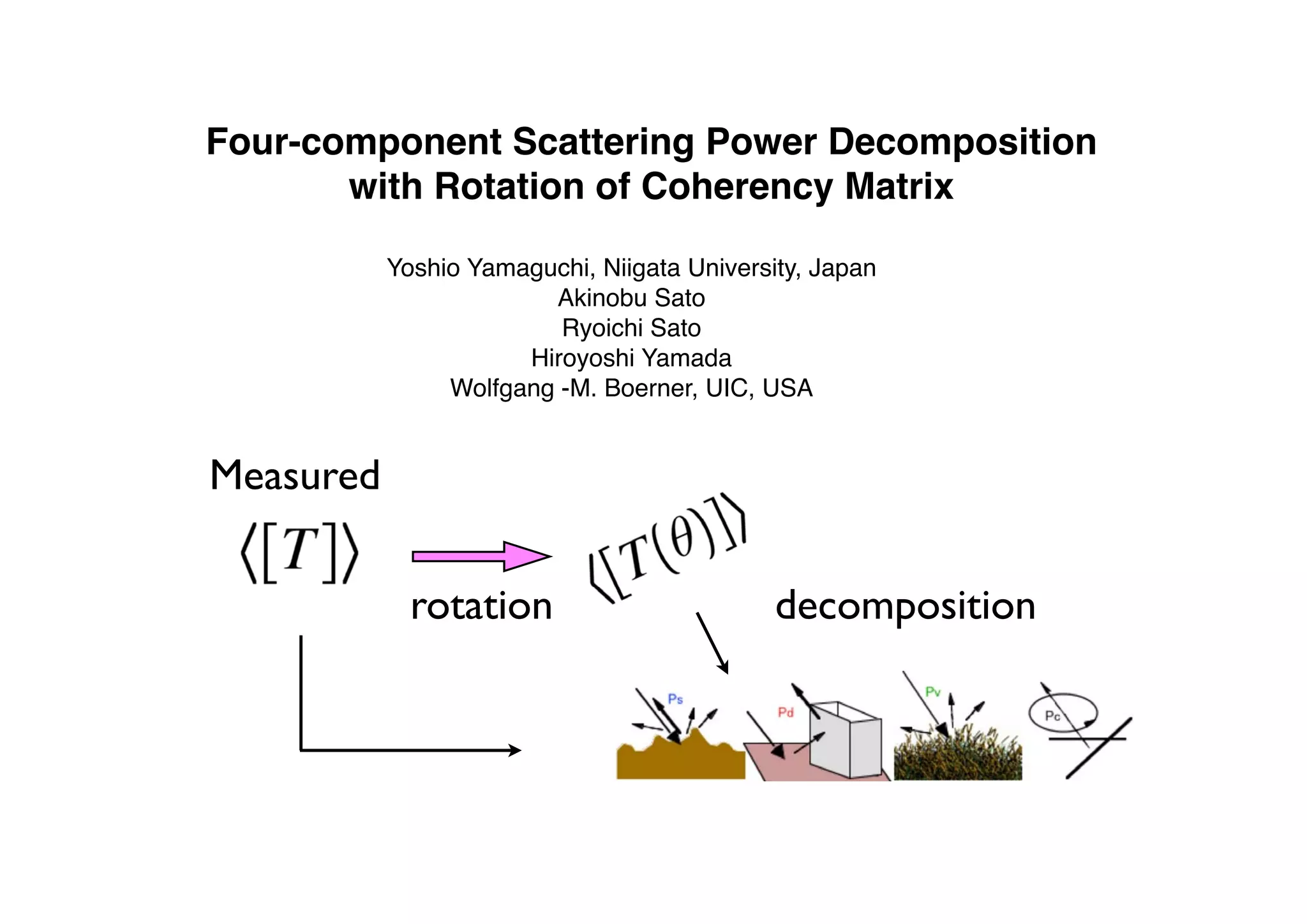
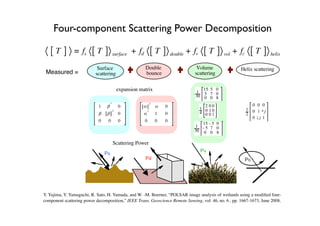
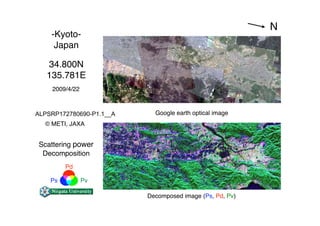
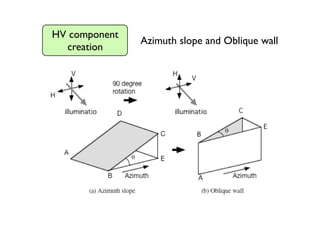
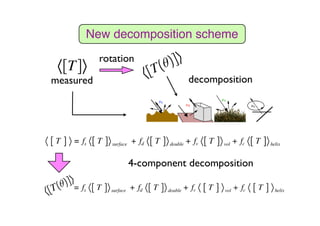
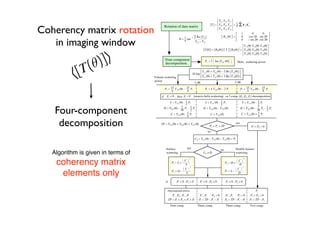
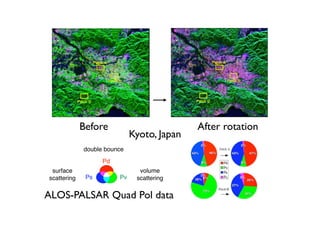
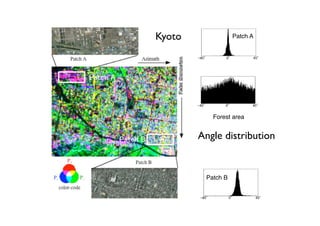
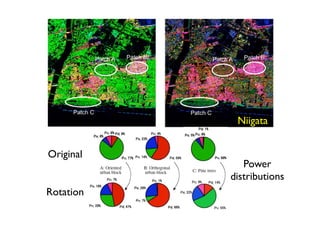
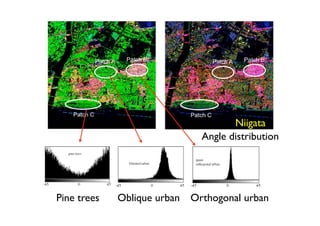
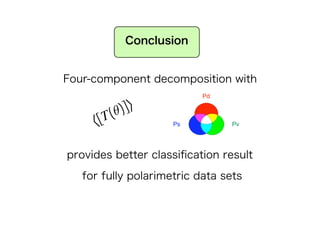
The document proposes a four-component scattering power decomposition method with rotation of the coherency matrix. This improves upon existing decomposition methods by minimizing the HV component through rotation, resulting in better separation of surface, double bounce, volume, and helix scattering mechanisms. The new method is applied to fully polarimetric SAR data sets to provide improved classification results.

1. Four-component Scattering Power Decomposition
with Rotation of Coherency Matrix
Yoshio Yamaguchi, Niigata University, Japan
Akinobu Sato
Ryoichi Sato
Hiroyoshi Yamada
Wolfgang -M. Boerner, UIC, USA
Measured
rotation decomposition

2. Four-component Scattering Power Decomposition
Surface Double Volume Helix scattering
Measured = scattering bounce scattering
expansion matrix 15 5 0
1 5 7 0
30 0 0 8
* 2
1 0 0 2 00 0 0 0
2
1 0 10 1 0 1 +j
0 *
1 0 4 0 01 2
0 +j 1
0 0 0 0 0 0
15 - 5 0
1 -5 7 0
30 0 0 8
Scattering Power
Y. Yajima, Y. Yamaguchi, R. Sato, H. Yamada, and W. -M. Boerner, “POLSAR image analysis of wetlands using a modified four-
component scattering power decomposition,” IEEE Trans. Geoscience Remote Sensing, vol. 46, no. 6 , pp. 1667-1673, June 2008.

3. N
-Kyoto-
Japan
34.800N
135.781E
2009/4/22
ALPSRP172780690-P1.1__A Google earth optical image
© METI, JAXA
Scattering power
Decomposition
Pd
Ps Pv
Decomposed image (Ps, Pd, Pv)

4. Concept for new decomposition
Too much green in urban area
Radar line of sight
Deorientation
S
Pd
T T
Ps Pv
Minimization of the HV component by rotation

5. HV component
Azimuth slope and Oblique wall
creation

6. Rotation of Coherency Matrix
Ensemble average in window
1 0 0
Rp ( ) = 0 cos 2 sin 2
0 – sin 2 cos 2

7. Minimization of T33 component
T 33 = T 33 cos 2 2 Re T 23 sin 4 + T 22 sin 22
Rotation angle
2 Re T23
= 1 tan - 1
4 T 22 T 33 Same as azimuth
slope angle

8. Coherency matrix elements after T33 rotation
Major terms for 4-comp. decomposition
Unchanged
Pure imaginary : Best fit to Helix scattering
Minor terms
2 = 1 tan - 1 2 Re T23
2 T22 T33

9. New decomposition scheme
rotation
measured decomposition
4-component decomposition

10. T11 T12 T 13 n
T = T21 T22 T 23 = 1
†
Coherency matrix rotation
n kp kp
Rotation of data matrix
T31 T32 T 33
1 0 0
- 1 2 Re T 23 Rp ( ) = 0 cos 2 sin 2
in imaging window
= 1 tan 0 – sin 2 cos 2
4 T 22 T 33
T 11 T 12 T 13
†
T = R P( ) T RP( ) = T 21 T 22 T 23
T 31 T 32 T 33
Four-component Pc = 2 Im T 23 ( )
decomposition Helix scattering power
T 11 ( ) + T 22 ( ) – 2 Re T12( )
10 log
Volume scattering T11 ( ) + T 22 ( ) + 2 Re T 12( )
power 2 dB
- 2 dB
Pv = 15 T 33 ( ) – 15 Pc Pv = 4 T 33 ( ) – 2 Pc Pv = 15 T 33 ( ) – 15 Pc
4 8 4 8
if Pv < 0 , then Pc = 0 (remove helix scattering) 3 comp. (Ps, Pd, Pv ) decomposition
S = T 11 ( ) - 1 Pv S = T 11 ( ) - 1 Pv S = T 11 ( ) - 1 Pv
2 2 2
Four-component D = T 22 ( ) - 7 Pv - 1 Pc
30 2
C = T 12 ( ) - 1 Pv
6
D = T 22 ( ) - T 33 ( )
C = T 12 ( )
D = T 22 ( ) - 7 Pv - 1 Pc
30
C = T 12 ( ) + 1 Pv
6
2
decomposition TP = T 11 ( ) + T 22 ( ) + T 33 ( )
Pv + Pc > TP
yes
Ps = Pd = 0
no
C 0 = T 11 ( ) – T 22 ( ) – T33 ( ) + Pc
Surface yes Double bounce
no
Algorithm is given in terms of scattering C0 > 0 scattering
coherency matrix
2 2
C C
Ps = S + Pd = D +
S D
2 2
C C
elements only Pd = D –
S
Ps = S –
D
if Ps > 0 , Pd > 0 Ps > 0 , Pd < 0 Ps < 0 , Pd > 0
Decomposed power Pc
Ps , Pd , Pv , Pc Pv , Pc Pd = 0 Pv , Pc Ps = 0 Ps = Pd = 0
TP = Ps + Pd + Pv + Pc Ps = TP – Pv – Pc Pd = TP – Pv – Pc Pv = TP – Pc
Four comp. Three comp. Three comp. Two comp.

11. Before After rotation
Kyoto, Japan
double bounce
Pd
surface volume
scattering Ps Pv scattering
ALOS-PALSAR Quad Pol data

12. Kyoto Patch A
Forest area
Angle distribution
Patch B

13. Niigata
Original
Power
distributions
Rotation

14. Niigata
Angle distribution
Pine trees Oblique urban Orthogonal urban

15. Pi-SAR-X
Niigata Japan
Angle distribution +4 -20
Patch E ° Patch D -20°

16. Before After rotation
L-band Pi-SAR data: Downtown Niigata, JAPAN
2007-10-04 (5*5 window)

17. Before After T33 rotation
Beijing, China

18. Conclusion
Four-component decomposition with
Pd
Ps Pv
provides better classification result
for fully polarimetric data sets