The document discusses mean-field models of interacting spins with and without growth. Mean-field models without growth are characterized by a single variable and spins flip independently of system size. Models with growth are characterized by two variables and include spins added from a reservoir at a rate that may depend on the system variables. The voter model and Glauber-Ising model are discussed as examples both with and without constant growth, where the voter model exhibits noise-induced bi-stability with growth.

1. Growth driven dynamics in mean-field
models of interacting spins
Richard G. Morris* and Tim Rogers†
* Theoretical Physics, The University of Warwick, Coventry, UK
†
Mathematics, The University of Bath, Bath, UK

2. Growth

7. How do physicists model growth?

9. Downloaded by [University of Warwick] at 04:32 20 Feb
phenomenon that has been studied for many decades, however, by metallurgists, is
Figure 2. Monte Carlo simulation of domain growth in the d ˆ 2 Ising model at T ˆ 0
(taken from Kissner [8]). The system size is 256 £ 256, and the snapshots correspond
to 5, 15, 60 and 200 Monte Carlo steps per spin after a quench from T ˆ 1.
Kissner J. G., Ph. D., The University of Manchester (1992)

10. What if growth cannot be separated
from relaxation?

11. What if growth cannot be separated
from relaxation?
↓
↑
↑
↓
↓
↓
↓
↑
↑
↓
↓
↓
↑
↓
↑
↑
↓
↓
↑
↓
↑
↑
↑
↓
↑
↓
↑
↓
↓
↓

12. What if growth cannot be separated
from relaxation?
↓
↑
↓
↓
↓
↓
↑
↑
↓
↓
↓
↑
↓
↑
↑
↓
↓
↑
↓
↑
↓
↑
↑
↑
↓
↑
↓
↑
↓
↓
↓

13. What if growth cannot be separated
from relaxation?
↓
↑
↓
↓
↓
↓
↑
↑
↓
↓
↓
↑
↓
↑
↑
↓
↓
↑
↓
↑
↓
↑
↑
↓
↓
↓
↓
↑
↓
↓
↓

14. What if growth cannot be separated
from relaxation?
↓
↑
↑
↓
↓
↓
↓
↑
↑
↓
↓
↓
↓
↑
↓
↑
↑
↓
↓
↑
↑
↓
↑
↑
↓
↓
↓
↓
↓
↑
↓
↓
↓

15. What if growth cannot be separated
from relaxation?
↓
↑
↑
↓
↓
↓
↓
↑
↑
↓
↓
↓
↓
↓
↓
↑
↑
↓
↓
↑
↑
↓
↑
↑
↓
↓
↓
↓
↓
↓
↓
↓
↓

16. What if growth cannot be separated
from relaxation?
↓
↓
↑
↑
↓
↓
↓
↓
↓
↑
↑
↓
↓
↓
↓
↓
↓
↑
↑
↓
↓
↑
↓
↓
↑
↑
↓
↓
↓
↓
↓
↓
↓
↓
↓

17. What if growth cannot be separated
from relaxation?
↓
↓
↓
↑
↑
↑
↓
↓
↓
↓
↓
↑
↑
↓
↓
↓
↓
↓
↓
↑
↑
↑
↓
↓
↓
↓
↓
↑
↑
↓
↓
↓
↓
↑
↓
↓
↑
↓
↓
↑
↑
↓
↓
↑
↑
↓
↓
↓
↓
↑
↓
↓
↑
↓
↓
↑
↑
↓
↓
↑
↑
↓
↓
↓
↓
↓
↑
↑
↓
↓
↓
↓
↑
↓
↓
↓
↑
↑
↓
↓
↓
↓
↑
↑
↓
↓
↓
↓
↑
↓
↓
↓
↑
↑
↓
↓
↓
↑
↓
↑
↓
↑
↑
↑
↑
↑
↑
↓
↑
↑
↑
↓
↓
↑
↓
↑
↓
↑
↑
↑
↑
↑
↑
↓
↑
↑
↑
↓
↓
↓
↓
↑
↓
↓
↑
↓
↓
↓
↓
↓
↑
↓
↓
↓
↓
↓
↓
↑
↓
↓
↑
↓
↓
↓
↓
↓
↑
↓
↓
↓

18. What if growth cannot be separated
from relaxation?
↓
↑
↓
↓
↑
↑
↓
↑
↑
↓

19. Mean-field models

20. Mean-field models
Non-growing

21. Mean-field models
Non-growing
•
Spins:
1,
...,
N
2 { 1, +1}

22. Mean-field models
Non-growing
•
•
Spins:
1,
...,
N
2 { 1, +1}
N
X
1
Characterised by one variable: x =
N i=1
i

23. Mean-field models
Non-growing
•
•
•
Spins:
1,
...,
N
2 { 1, +1}
N
X
1
Characterised by one variable: x =
N i=1
i
Rate of flipping individuals spin is independent of
the system size.

24. Mean-field models
Non-growing
•
•
•
•
Spins:
1,
...,
N
2 { 1, +1}
N
X
1
Characterised by one variable: x =
N i=1
i
Rate of flipping individuals spin is independent of
the system size.
✓ ◆
1
Stochastic evolution of jump size O
N

25. Mean-field models
Growing

26. Mean-field models
Growing
•
Spins:
1,
...,
N (t)
2 { 1, +1}

27. Mean-field models
Growing
1,
...,
2 { 1, +1}
•
Spins:
•
Characterised by two variables: (x, s) or (u, v)
N (t)

28. Mean-field models
Growing
1,
...,
2 { 1, +1}
•
Spins:
•
Characterised by two variables: (x, s) or (u, v)
•
Rate of flipping individuals spin is still independent
of the system size.
N (t)

29. Mean-field models
Growing
1,
...,
2 { 1, +1}
•
Spins:
•
Characterised by two variables: (x, s) or (u, v)
•
Rate of flipping individuals spin is still independent
of the system size.
•
Asymptotics now defined in terms of N0 ⌘ N (t = 0)
i.e., a lower bound on N
N (t)

30. Mean-field models
Growth mechanism

31. Mean-field models
Growth mechanism
•
Spins added from a reservoir at a rate:

32. Mean-field models
Growth mechanism
•
Spins added from a reservoir at a rate:
•
Reservoir can be magnetised: gu , gv

33. Mean-field models
Growth mechanism
•
Spins added from a reservoir at a rate:
•
Reservoir can be magnetised: gu , gv
•
Rate of flipping individual spins: fu , fv

34. Mean-field models
Growth mechanism
•
Spins added from a reservoir at a rate:
•
Reservoir can be magnetised: gu , gv
•
Rate of flipping individual spins: fu , fv
•
Both gu , gv and fu , fv may depend on x

35. Mean-field models
Growth mechanism
•
Spins added from a reservoir at a rate:
•
Reservoir can be magnetised: gu , gv
•
Rate of flipping individual spins: fu , fv
•
Both gu , gv and fu , fv may depend on x
•
Effects of growth are subordinate to flips but still
macroscopic… ⇠ N ↵ , ↵ 2 ( 1, +1)

36. Mean-field models
Formal description

37. Mean-field models
Formal description

⇣
⌘
d
1/N0 +1/N0
P (u, v, t) = N0 Eu
Ev
1 vfv
dt
⇣
⌘
+1/N0
+ N0 E u
Ev 1/N0 1 ufu
⇣
⌘
1/N0
+ Eu
1 gu
⇣
⌘
1/N0
+ Ev
1 gv P (u, v, t)

38. Mean-field models
Formal description
Eu
1/N0
=1
1 @
1 @2
3
+
2 @u2 + O 1/N0
N0 @u 2N0

39. Mean-field models
Formal description
@
P (u, v, t) =
@t
✓
◆
@
@
vfv P (u, v, t)
@u @v
✓
◆
@
@
+
ufu P (u, v, t)
@u @v
✓
◆
1
@
@
gu +
gv
P (u, v, t)
N0 @u
@v
✓
◆2
1
@
@
(vfv + ufu ) P (u, v, t)
+
2N0 @u @v
+O
3
1/N0

40. Mean-field models
Formal description
du
= (vfv
dt
dv
= (ufu
dt
r
ufu + vfv
ufu ) +
gu +
⌘(t),
N0
N0
r
ufu + vfv
vfv ) +
gv
⌘(t)
N0
N0

41. Mean-field models
Formal description
ds
=
dt sN0
dx
=(1 x)fv
dt
+
(gu
sN0
s
(1
+ 2
(1 + x)fu
gv
x)
x)fv + (1 + x)fu
⌘(t) .
sN0

42. The Voter model

43. The Voter model
Non-growing

44. The Voter model
Non-growing
•
“Pick a neighbouring spin and copy it…”

45. The Voter model
Non-growing
•
“Pick a neighbouring spin and copy it…”
fu = (1
x)/2, fv = (1 + x)/2

46. The Voter model
Non-growing
•
“Pick a neighbouring spin and copy it…”
fu = (1
x)/2, fv = (1 + x)/2
dx p
= 2(1
d⌧
x2 ) ⌘(⌧ )

47. The Voter model
0.2
Non-growing
x
0
−0.2
0
dx p
= 2(1 x2 ) ⌘(⌧ )
50d⌧
100
150
200
t
0.2
x
0
−0.2
0
0.5
1
τ
1.5
2

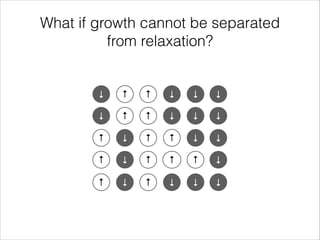
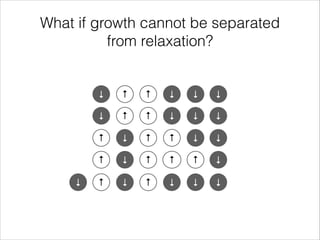
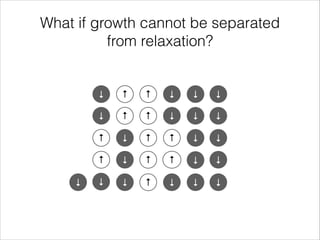
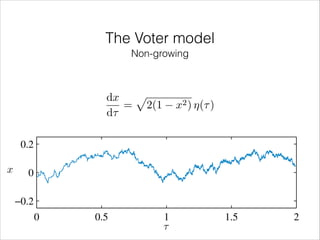
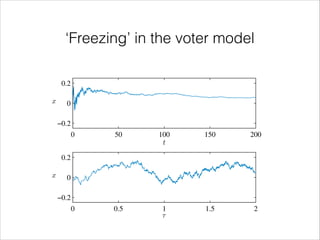
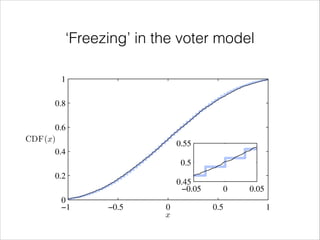
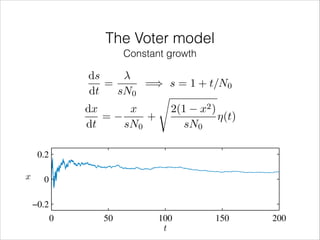
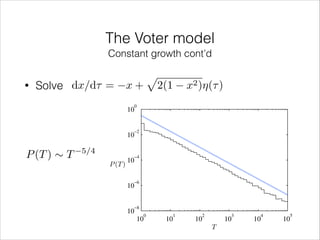
48. The Voter model
0.2
Non-growing
x
dx p
= 2(1
d⌧
0
−0.2
0
x2 ) ⌘(⌧ )
=) P1 (x) = [ (x1001) + (x +150 /2
1)]
50
200
t
0.2
x
0
−0.2
0
0.5
1
τ
1.5
2

49. The Voter model
Constant growth

50. The Voter model
Constant growth
•
Choose
=1

51. The Voter model
Constant growth
•
Choose
•
Zero net reservoir-magnetisation: gu = gv = 1/2
=1

52. The Voter model
Constant growth
•
Choose
•
Zero net reservoir-magnetisation: gu = gv = 1/2
=1
ds
=
=) s = 1 + t/N0
dt
sN0
s
dx
x
2(1 x2 )
=
+
⌘(t)
dt
sN0
sN0

53. The Voter model
Constant growth
ds
=
=) s = 1 + t/N0
dt
sN0
s
dx
x
2(1 x2 )
=
+
⌘(t)
dt
sN0
sN0
0.2
x
0
−0.2
0
50
100
t
150
200

54. The Voter model
Constant growth
ds
=
=) s = 1 + t/N0
dt
sN0
s
dx
x
2(1 x2 )
=
+
⌘(t)
dt
sN0
sN0
d⌧
1
dx
=
=)
=
dt
sN0
d⌧
p
x + 2(1
x2 )⌘(⌧ )

55. The Voter model
Constant growth
ds
=
=) s = 1 + t/N0
dt
sN0
s
dx
x
2(1 x2 )
=
+
⌘(t)
dt
sN0
sN0
d⌧
1
dx
=
=)
=
dt
sN0
d⌧
•
p
x + 2(1
“Noise-induced bi-stability!”
x2 )⌘(⌧ )

56. The Voter model
Constant growth cont’d

57. The Voter model
Constant growth cont’d
•
Solve dx/d⌧ =
x+
p
2(1
x2 )⌘(⌧ )

58. The Voter model
Constant growth cont’d
•
Solve dx/d⌧ =
x+
p
2(1
x2 )⌘(⌧ )

59. The Voter model
Constant growth cont’d
•
Solve dx/d⌧ =
P (x, t) =
x+
✓3 sin
p
1
2(1
x2 )⌘(⌧ )
(x), (N0 + t)
p
⇡ 1 x2
4

60. The Voter model
Constant growth cont’d
•
Solve dx/d⌧ =
x+
p
P1 (x) = ⇡
2(1
1
(1
x2 )⌘(⌧ )
2
x )
1/2

61. The Voter model
Constant growth cont’d
•
Solve dx/d⌧ =
x+
p
P1 (x) = ⇡
2(1
1
x2 )⌘(⌧ )
2
1/2
(1 x )
✓
◆
1
N0
0
P (T ) =
✓1 0,
2⇡(N0 + T )
N0 + T

62. The Voter model
Constant growth cont’d
•
Solve dx/d⌧ =
x+
p
P1 (x) = ⇡
2(1
1
P (T ) ⇠ T
(1
5/4
x2 )⌘(⌧ )
2
x )
1/2

63. The Voter model
Constant growth cont’d
•
Solve dx/d⌧ =
x+
0
10
p
2(1
x2 )⌘(⌧ )
−2
10
P (T ) ⇠ T
5/4
−4
P (T )
10
−6
10
−8
10
0
10
1
10
2
3
10
10
T
4
10
10
5

64. The Glauber-Ising model

65. The Glauber-Ising model
Non-growing

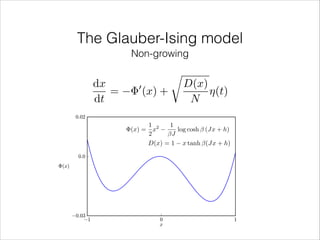
66. The Glauber-Ising model
Non-growing
P ({ }) = e
H[{ }]
/Z

67. The Glauber-Ising model
Non-growing
P ({ }) = e
Z=
X
x
e
H[{ }]
/Z
H[{ }]

68. The Glauber-Ising model
Non-growing
P ({ }) = e
Z=
H [{ }] =
X
e
H[{ }]
/Z
H[{ }]
x
N
X
J
N
hi,ji
i j
h
N
X
i=1
i

69. The Glauber-Ising model
Non-growing
H(x)
P (x) = e
Z=
H (x) =
X
e
/Z
H(x)
x
J
2
Nx
2
1
N hx

70. The Glauber-Ising model
Non-growing
H(x)
P (x) = e
Z=
H (x) =
fu/d
X
e
/Z
H(x)
x
J
2
Nx
2
1
N hx
1
= [1 ⌥ tanh (Jx + h)]
2

71. The Glauber-Ising model
Non-growing

72. The Glauber-Ising model
Non-growing
dx
=
dt
0
(x) +
r
D(x)
⌘(t)
N

73. The Glauber-Ising model
Non-growing
dx
=
dt
0
(x) +
r
D(x)
⌘(t)
N
1 2
1
(x) = x
log cosh (Jx + h)
2
J
D(x) = 1 x tanh (Jx + h)

74. The Glauber-Ising model
Growing

75. The Glauber-Ising model
Growing
•
Rescaling of time no-longer works due to
deterministic “drift” terms:

76. The Glauber-Ising model
Growing
•
Rescaling of time no-longer works due to
deterministic “drift” terms:
dx
= tanh (Jx + h)
dt
x + O (1/N0 )

77. The Glauber-Ising model
Growing
•
Rescaling of time no-longer works due to
deterministic “drift” terms:
dx
= tanh (Jx + h)
dt
•
x + O (1/N0 )
Separation of of timescales implies instantaneous
size-dependent escape rate:

78. The Glauber-Ising model
Growing
•
Rescaling of time no-longer works due to
deterministic “drift” terms:
dx
= tanh (Jx + h)
dt
x + O (1/N0 )
Separation of of timescales implies instantaneous
size-dependent escape rate:
s
⇢ Z x1 0
00 (x )| 00 (x )|D(x )
(⇠)
0
1
0
(s) =
exp
s
d⇠
2 D(x )
4⇡
1
x0 D(⇠)
•

79. The Glauber-Ising model
Growing cont’d

80. The Glauber-Ising model
Growing cont’d
•
Survivor function:

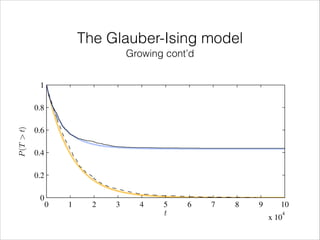
81. The Glauber-Ising model
Growing cont’d
•
Survivor function:
P (T
t) = exp
⇢ Z
t
0
[s(t )] dt
0
0

82. The Glauber-Ising model
Growing cont’d
•
Survivor function:
P (T
•
t) = exp
Constant growth:
⇢ Z
t
0
[s(t )] dt
0
0

83. The Glauber-Ising model
Growing cont’d
•
Survivor function:
P (T
•
t) = exp
⇢ Z
t
0
[s(t )] dt
0
0
Constant growth:
P (T
t) = exp
⇢
AN0 B ⇣
e 1
B
e
B t/N0
⌘
A = (0), B = 0 (0)/(0) < 0

84. The Glauber-Ising model
Growing cont’d
•
Survivor function:
P (T
•
t) = exp
⇢ Z
t
0
[s(t )] dt
0
0
Constant growth:
P (T
1) > 0
A = (0), B = 0 (0)/(0) < 0

85. The Glauber-Ising model
Growing cont’d
1
P (T > t)
0.8
0.6
0.4
0.2
0
0
1
2
3
4
5
t
6
7
8
9
10
4
x 10

87. …back to the voter model

88. …back to the voter model

89. …back to the voter model
•
What if
↵
= N …?

90. …back to the voter model
↵
= N …?
•
What if
•
Rescale time:
n
1
↵
⌧=
N0
↵
⇥
(1
↵) t +
↵
N0
⇤ ↵↵ 1 o
1

91. …back to the voter model
↵
= N …?
•
What if
•
Rescale time:
n
1
↵
⌧=
N0
↵
⇥
(1
↵) t +
↵
N0
↵
N0
⇤
⌧ = lim ⌧ =
t!1
↵
⇤ ↵↵ 1 o
1

92. ‘Freezing’ in the voter model

93. ‘Freezing’ in the voter model
•
Growing disc:
=
p
N

94. ‘Freezing’ in the voter model
•
Growing disc:
•
=
p
N
Replication:
gu = u = (1 + x)/2, gv = v = (1
x)/2

95. ‘Freezing’ in the voter model
•
Growing disc:
•
=
p
N
Replication:
gu = u = (1 + x)/2, gv = v = (1
⌧⇤ =
p
dx p
= 2 (1
d⌧
N0 /2
x2 )⌘(⌧ )
x)/2

96. ‘Freezing’ in the voter model
0.2
x
0
−0.2
0
50
100
t
150
200
0
0.5
1
τ
1.5
2
0.2
x
0
−0.2

97. ‘Freezing’ in the voter model
1
0.8
0.6
CDF(x)
0.55
0.4
0.5
0.2
0.45
−0.05
0
−1
−0.5
0
x
0
0.5
0.05
1

98. Wrap-up

99. Wrap-up

100. Wrap-up
•
Growth affects the dynamics of even the simplest
spin-models.

101. Wrap-up
•
Growth affects the dynamics of even the simplest
spin-models.
•
Seems pretty cool… absorbing/meta-stable
‘switch’.

102. Wrap-up
•
Growth affects the dynamics of even the simplest
spin-models.
•
Seems pretty cool… absorbing/meta-stable
‘switch’.
•
Going forward: what can we say about spatial
models?

103. Wrap-up
•
Growth affects the dynamics of even the simplest
spin-models.
•
Seems pretty cool… absorbing/meta-stable
‘switch’.
•
Going forward: what can we say about spatial
models?
•
What do you think / can you help?