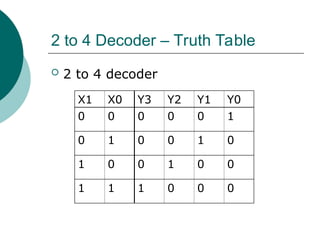
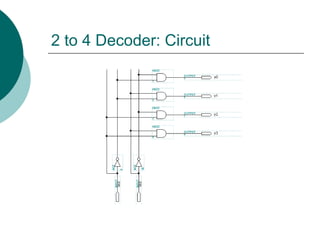
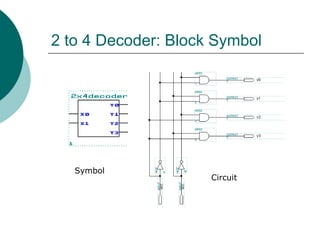
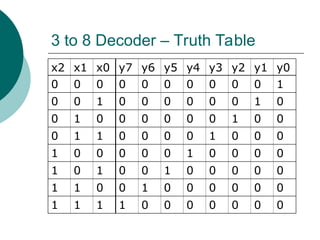
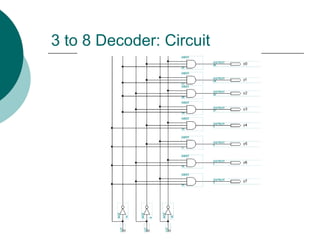
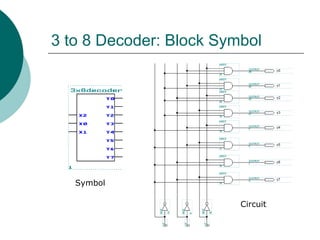
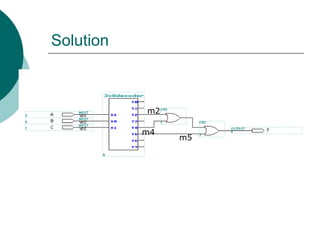
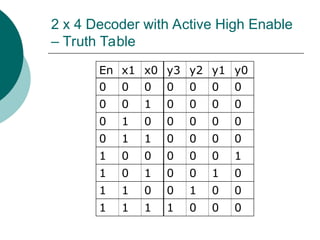
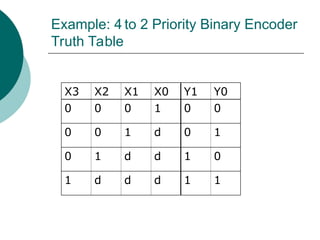
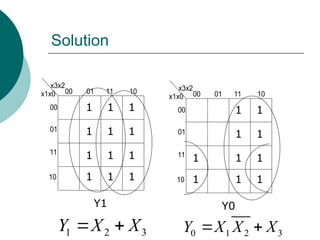
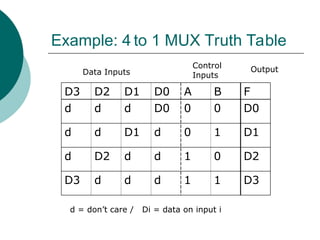
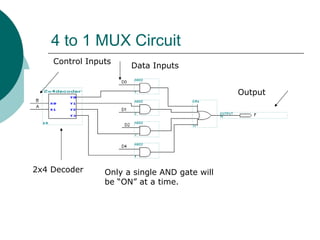
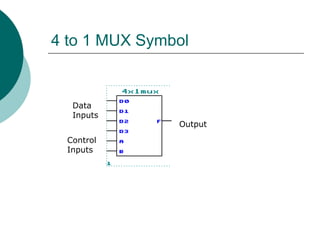
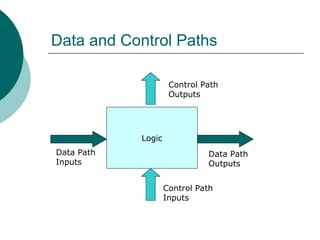
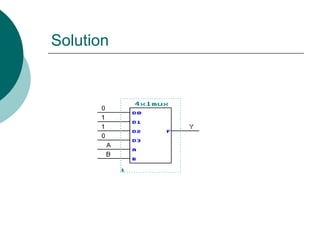
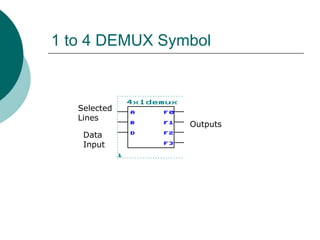
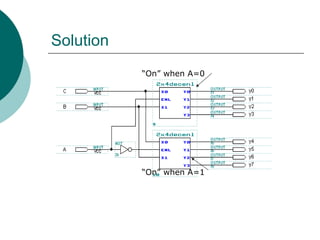
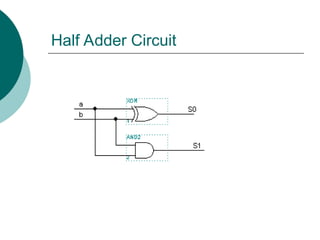
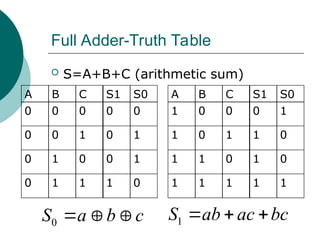
The document discusses modular combinational logic and focuses on decoders, encoders, multiplexers, and demultiplexers. It provides examples, truth tables, and equations for 2 to 4 and 3 to 8 decoders as well as encoders, highlighting their functionalities and circuit designs. Additionally, it explains the role of multiplexers and demultiplexers in data selection and distribution, along with examples of arithmetic elements like half and full adders.

1. Chapter 4
Modular Combinational Logic

2. Decoders

3. Decoders
 n to 2n
decoder
 n inputs
 2n
outputs
 For each input, one and only one output
will be active.
 Uses:
 “Minterm generator”
 Wordline (memory) circuit
 Code conversion
 Routing data

4. 2 to 4 Decoder Example

5. 2 to 4 Decoder – Truth Table
 2 to 4 decoder
X1 X0 Y3 Y2 Y1 Y0
0 0 0 0 0 1
0 1 0 0 1 0
1 0 0 1 0 0
1 1 1 0 0 0

6. 2 to 4 Decoder Equations
0 1 0
1 1 0
2 1 0
3 1 0
Y X X
Y X X
Y X X
Y X X





7. 2 to 4 Decoder: Circuit

8. 2 to 4 Decoder: Block Symbol
Symbol
Circuit

9. 3 to 8 Decoder Example

10. 3 to 8 Decoder – Truth Table
x2 x1 x0 y7 y6 y5 y4 y3 y2 y1 y0
0 0 0 0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0 0 1 0
0 1 0 0 0 0 0 0 1 0 0
0 1 1 0 0 0 0 1 0 0 0
1 0 0 0 0 0 1 0 0 0 0
1 0 1 0 0 1 0 0 0 0 0
1 1 0 0 1 0 0 0 0 0 0
1 1 1 1 0 0 0 0 0 0 0

11. 3 to 8 Decoder Equations
0 2 1 0
1 2 1 0
2 2 1 0
3 2 1 0
Y X X X
Y X X X
Y X X X
Y X X X




4 2 1 0
5 2 1 0
6 2 1 0
7 2 1 0
Y X X X
Y X X X
Y X X X
Y X X X





12. 3 to 8 Decoder: Circuit

13. 3 to 8 Decoder: Block Symbol
Symbol
Circuit

14. Design Example

15. Example
 Using only a 3x8 decoder and two-
input OR gates, design a logic
circuit which implements the
following Boolean equation
   
, , 2,4,5
F a b c m


16. Solution
m2
m4
m5

17. 2 to 4 Decoder with Enable

18. 2x4 Decoder with Enable
 Enable is abbreviated as EN
 EN is called a Control Signal
 Control Signals can be
 Active High Signal
 EN = 1 – Turns “ON” Decoder
 Active Low Signal
 EN=0 – Turns “ON” Decoder

19. 2 x 4 Decoder with Active High Enable
– Truth Table
En x1 x0 y3 y2 y1 y0
0 0 0 0 0 0 0
0 0 1 0 0 0 0
0 1 0 0 0 0 0
0 1 1 0 0 0 0
1 0 0 0 0 0 1
1 0 1 0 0 1 0
1 1 0 0 1 0 0
1 1 1 1 0 0 0

20. 2 to 4 Decoder with Enable Equations
0 1 0
1 1 0
2 1 0
3 1 0
n
n
n
n
Y E X X
Y E X X
Y E X X
Y E X X





21. 2 to 4 Decoder with Enable Circuit

22. 2 to 4 Decoder with Enable Symbol

23. 2 x 4 Decoder with Active High Enable
– Truth Table (Short hand notation)
En x1 x0 y3 y2 y1 y0
0 d d 0 0 0 0
1 0 0 0 0 0 1
1 0 1 0 0 1 0
1 1 0 0 1 0 0
1 1 1 1 0 0 0
d = don’t care
En has “highest” priority.
If En=0, we “don’t care” about x1 or x0 because Y=0

24. 2 x 4 Decoder with Active Low Enable
– Truth Table (Short hand notation)
EnL x1 x0 y3 y2 y1 y0
1 d d 0 0 0 0
0 0 0 0 0 0 1
0 0 1 0 0 1 0
0 1 0 0 1 0 0
0 1 1 1 0 0 0
d = don’t care
En has “highest” priority.
If En=1, we “don’t care” about x1 or x0 because Y=0

25. 2 to 4 Decoder with Active Low Enable
Circuit

26. Design Example

27. Example
 Design a 3x8 decoder using only
2x4 decoders and NOT gates.

28. Solution
“On” when A=1
“On” when A=0

29. TPS Quiz

30. Encoders

31. Encoders
 Opposite of a decoder
 2n
to n encoder
 2n
inputs
 n outputs
 For each input, the circuit will
produce an “encoded” output

32. Example: 4 to 2 Binary Encoder
Truth Table
X3 X2 X1 X0 Y1 Y0
0 0 0 1 0 0
0 0 1 0 0 1
0 1 0 0 1 0
1 0 0 0 1 1
Assume only one input high at a time!!

33. 4 to 2 Encoder Equations
0 1 3
1 2 3
Y X X
Y X X
 
 

34. Problems with initial design
 Q: How do we tell the difference
between an input of all 0’s (i.e.
X=0) and X=1?
 A: Add another output (IA) that
indicates that the input is valid.
Let’s make IA active low.
0 1 2 3
IA X X X X
   

35. Problems with initial design
If IA = 1 => all lines are 0
If IA = 0 => at least one line is 1
 Q: What happens if more than one input
is high at the same time?
 A: Design a “priority” encoder that will
encode the input with the highest priority.
 Let’s set X3 with the highest priority,
followed by X2, X1, and X0

36. Example: 4 to 2 Priority Binary Encoder
Truth Table
X3 X2 X1 X0 Y1 Y0
0 0 0 1 0 0
0 0 1 d 0 1
0 1 d d 1 0
1 d d d 1 1

37. Solution
x3x2
x1x0 00 01 11 10
00
01
11
10
Y1
x3x2
x1x0 00 01 11 10
00
01
11
10
Y0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1 2 3
Y X X
  0 1 2 3
Y X X X
 

38. 4 to 2 Priority Encoder Equations
0 1 2 3
1 2 3
Y X X X
Y X X
 
 
0 1 2 3
IA X X X X
   

39. Multiplexer/Data Selectors
MUX
Very Important Module!!!

40. Multiplexer(MUX)/Data Selector
 N to 1 multiplexer
 n data input lines
 Log2(n) control inputs
 One output
 This circuit will “connect” the
selected input to the output. The
selected input is specified by a
decoding of the control inputs.

41. Example: 4 to 1 MUX Truth Table
D3 D2 D1 D0 A B F
d d d D0 0 0 D0
d d D1 d 0 1 D1
d D2 d d 1 0 D2
D3 d d d 1 1 D3
d = don’t care / Di = data on input i
Data Inputs
Control
Inputs
Output

42. 4 to 1 MUX Equation
0 1 2 3
F D AB D AB D AB D AB
   
3
0
i i
i
F D m


D’s are the DATA inputs, AB are control inputs and called
the “select” lines.

43. 4 to 1 MUX Circuit
2x4 Decoder Only a single AND gate will
be “ON” at a time.
Output
Control Inputs
Data Inputs

44. 4 to 1 MUX Symbol
Data
Inputs
Control
Inputs
Output

45. Data and Control Paths
Logic
Data Path
Inputs
Data Path
Outputs
Control Path
Inputs
Control Path
Outputs

46. MUX Applications

47. Example
 Using a 4x1 MUX, design a logic
circuit which implements:
Y a b
 
We have,
Y
0 1 2 3
Y D AB D AB D AB D AB
   

48. Example
 Using a 4x1 MUX, design a logic
circuit which implements:
Y a b
 
a b Y Dn
0 0 0 D0
0 1 1 D1
1 0 1 D2
1 1 0 D3
0 1 1 0
Y AB AB AB AB AB AB
     

49. Solution

50. Multibit Multiplexers

51. Multi-bit Multiplexers
 J-bit nx1 mux
sel
d0
d1
…
dn-1
d2 F
J bits
deep
log2n
J bits
deep
   
0
j
i i
i
F j D j m


j=0 to 3
This is just J separate nx1 multiplexers

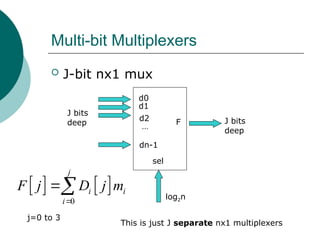
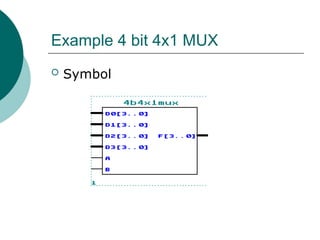
52. Example 4-bit 4x1 MUX
A B
D0[3..0]
D1[3..0]
D3[3..0]
D2[3..0]
F[3..0] 4 bits
deep
D0[3..0]
D1[3..0]
D2[3..0]
D3[3..0]
A B
F[3..0]
   
3
0
i i
i
F j D j m


j=0 to 3 This is just 4 separate 4x1 muxes

53. Example
 4-bit 4x1 MUX
         
0 1 2 3
0 0 0 0 0
F D AB D AB D AB D AB
   
         
0 1 2 3
1 1 1 1 1
F D AB D AB D AB D AB
   
         
0 1 2 3
2 2 2 2 2
F D AB D AB D AB D AB
   
         
0 1 2 3
3 3 3 3 3
F D AB D AB D AB D AB
   
Bit 0
Bit 3
Bit 2
Bit 1

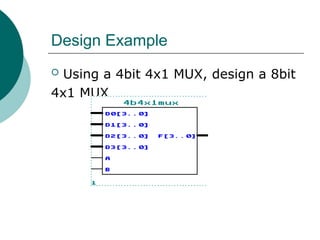
54. Example 4 bit 4x1 MUX
 For the jth output, we have
D0[j]
D1[j]
D2[j]
D3[j]
A
B
F[j]

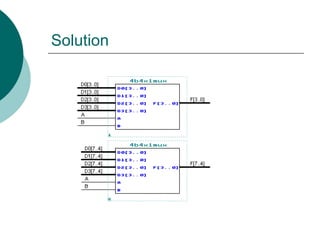
55. Example 4 bit 4x1 MUX
 For the bit 0 output, we have
D0[0]
D1[0]
D2[0]
D3[0]
A
B
F[0]

56. Example 4 bit 4x1 MUX
 For the bit 1 output, we have
D0[1]
D1[1]
D2[1]
D3[1]
A
B
F[1]

57. Example 4 bit 4x1 MUX
 For the bit 2 output, we have
D0[2]
D1[2]
D2[2]
D3[2]
A
B
F[2]

58. Example 4 bit 4x1 MUX
 For the bit 3 output, we have
D0[3]
D1[3]
D2[3]
D3[3]
A
B
F[3]

59. Example 4 bit 4x1 Mux
F[0]
F[1]
F[2]
F[3]
Complete Circuit
Bit 0
Bit 1
Bit 2
Bit 3

60. Example 4 bit 4x1 MUX
 Symbol

61. Design Example
 Using a 4bit 4x1 MUX, design a 8bit
4x1 MUX

62. Solution

63. DeMultiplexers/
Data Distributors

64. Demultiplexer/Data Distributor
 Opposite of a multiplexer
 1 to N demultiplexer
 1 data input
 N data outputs
 Log2(n) control inputs
 This circuit will “connect” a data
input to one and only one output.
The selected output is specified by a
decoding of the control inputs.

65. Example: 1 to 4 DeMUX Truth Table
D A B F3 F2 F1 F0
D 0 0 0 0 0 D
D 0 1 0 0 D 0
D 1 0 0 D 0 0
D 1 1 D 0 0 0
d = don’t care / Di = data on input i

66. 1 to 4 DeMUX Equations
3 3
F DAB Dm
 
j j
F Dm

D is the DATA inputs, AB are control inputs and called
the “select” lines.
1 1
F DAB Dm
 
2 2
F DAB Dm
 
0 0
F DAB Dm
 

67. 1 to 4 DEMUX Circuit
Only 1 AND gate will
be “ON”
2x4 Decoder
Only one
F will be
active

68. 1 to 4 DEMUX Symbol
Data
Input
Selected
Lines
Outputs

69. Example
 Design a 3x8 decoder using only
2x4 decoders and NOT gates.

70. Solution
“On” when A=1
“On” when A=0

71. TPS Quiz

72. Basic Arithmetic Elements
Half Adder

73. Half Adder-Truth Table
 S=A+B (arithmetic sum)
A B S1 S0
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0
0
S a b
 
1
S ab


74. Half Adder Circuit

75. Full Adder-Truth Table
 S=A+B+C (arithmetic sum)
A B C S1 S0
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
0
S a b c
   1
S ab ac bc
  
A B C S1 S0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1

76. Full Adder
0
S a b c
  
1
S ab ac bc
  
You can show!!!
 
1
S ab c a b
  

77. Synthesis
(0)
S A B C
  
Logic Equation
Logic Circuit

78. Synthesis
 
(1)
S AB C A B
  
Logic Equation
Logic Circuit

79. 17
AND2 18
OR2
19 cout
OUTPUT
16
AND2
VCC
14 Cin INPUT
VCC
13 B INPUT
10
XOR
11
XOR
15 sum
OUTPUT
VCC
12 A INPUT
Synthesis
Full Adder Circuit
S(0)
S(1)
C
A
B
S(0)
S(1)
Simulation

80. Verification
S(0)
S(1)
We verify the circuit via a simulation
Logic Simulation
Inputs
Outputs
S 00 01 01 10 01 01 01 11

81. 17
AND2 18
OR2
19 cout
OUTPUT
16
AND2
VCC
14 Cin INPUT
VCC
13 B INPUT
10
XOR
11
XOR
15 sum
OUTPUT
VCC
12 A INPUT
Verification Summary
S(0)
S(1)
C
A
B
S(0)
S(1)
Simulation
Circuit

82. Documentation
17
AND2 18
OR2
19 cout
OUTPUT
16
AND2
VCC
14 Cin INPUT
VCC
13 B INPUT
10
XOR
11
XOR
15 sum
OUTPUT
VCC
12 A INPUT
S(0)
S(1)
C
A
B
FullAdder
C
A
B
S(0)
S(1)
Block Diagram

83. Ripple Carry Adder

84. Conceptualization
 4-bit adder (worst case)
1111
1111
11110
1
1
1
For the “worst case” we need to add
three bits to generate a single output bit
with a possible carry out.
Can we use our single bit adder for this?

85. Ripple Carry Adder
 We can cascade several full adders
to create a ripple carry adder
 The circuit gets its name because
the carry bit “ripples” from one bit
position to the next

86. Conceptualization
FullAdder
C
A
B
S(0)
S(1)
FullAdder
C
A
B
S(0)
S(1)
First, let’s look at two bits
A(0)
B(0)
B(1)
A(1)
Sum(0)
Sum(1)
What about the carry?

87. Conceptualization
FullAdder
C
A
B
S(0)
S(1)
FullAdder
C
A
B
S(0)
S(1)
Let’s connect the two full adders
A(0)
B(0)
B(1)
A(1)
S(0)
S(1)
Set carry in for first bit to 0. Why?
Cout
Cin
0

88. Analysis
FullAdder
C
A
B
S(0)
S(1)
FullAdder
C
A
B
S(0)
S(1)
Let’s test this for a few cases:
0
0
0
0
0
0
0
0
0
0
00
00
000
Correct!!!
Rule of thumb: Always test simple cases first!!

89. Analysis
FullAdder
C
A
B
S(0)
S(1)
FullAdder
C
A
B
S(0)
S(1)
Let’s test this for the a few cases
0
1
1
1
1
1
1
0
1
1
11
11
110
Correct!!!

90. Analysis
FullAdder
C
A
B
S(0)
S(1)
FullAdder
C
A
B
S(0)
S(1)
Let’s test this for the a few cases
1
1
0
0
0
1
1
1
0
0
01
01
010
Correct!!!

91. Four Bit “Ripple” Adder
Carry in
Carry out

92. Logic Simulation

93. 8-bit Ripple Carry Adder
 Use two 4-bit adders

94. 16-bit Ripple Carry Adder
 Use two 8-bit adders

95. Subtraction Circuit

96. Subtraction Circuit
 Calculate 2’s complement of B
 Add –B to A
ADDER
INV
A
B
S
1
Cin
A
B
  1
S A B A B A B
       
B
1

1
S A B
  

97. Add/Sub Circuit

98. Add/Sub Circuit Module
Add/Sub
Module
A
B
S
Add
A
B
Add
S

99. Function Table for Add/Sub Module
Add Functional
Result
0 S=A+B
1 S=A-B
Add is a control input. It is active low. This means
that the module will compute A+B when Add=0. It
will compute A-B when Add=1.

100. Add/Sub Circuit
Design using Modules

101. Add/Sub Circuit
ADDER
INV
2x1
MUX
A
B
S
B
B
A
S Cin
A
Add

102. Add/Sub Circuit
ADDER
INV
2x1
MUX
A
B
S
B
B
A
S Cin
A
Add
Add operation. Add=0
0 0
S A B
 

103. Add/Sub Circuit
ADDER
INV
2x1
MUX
A
B
S
B
B
A
S Cin
A
Add
Sub operation. Add=1
1 1
1
S A B
  
B

104. TPS Quiz
17-18

105. Overflow/Underflow Detection

106. Numerical Overflow/Underflow
 2’s complement number
 We have S=A+B
 Range of sum
 Overflow occurs if
 Underflow occurs if
1 1
2 2 1
n n
S
 
   
1
2 1
n
S 
 
1
2n
S 
 

107. Example: Overflow
 Let n=4, Range is
 Let A=$7, B=$7, then S=$7+
$7=$E, but $E=%1110 = -2, so
Overflow has occurred.
8 7
S
  
3 3
2 2 1
S
   

108. Example: Overflow
 Let’s examine this more closely
-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7
+7
So, overflow is the same as “wrap around.”
8,9,A,B,C,D,E,F,0,1,2,3,4,5,6,7

109. Example: Underflow
 Let n=4, let A=-7 and B=-7,
 in 2’s complement, A=B=$9,
S=$9+$9=$12=$02
 so underflow has occurred.

110. Example: Underflow
 Let’s examine this more closely
-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7
+6
So, underflow is the same as “wrap around.”
+1

111. Overflow/Underflow Detection
 How do we detect overflow and
underflow?
 First adding a positive to a negative
number is always OK.
 4 bit example: 7 + (-8) = -1
 Let’s examine the sum of the MSB’s to
determine overflow and underflow.
 Set V=1, if overflow/underflow occurs

112. Examination of MSB
b a cin S Co V Explanation
0 0 0 0 0 0 A+B < 2n-1
(OK)
0 0 1 1 0 1 A+B>2n-1
-1 (overflow)
0 1 0 1 0 0 -A+B (OK)
0 1 1 0 1 0 -A+B (OK)
1 0 0 1 0 0 A-B (OK)
1 0 1 0 1 0 A-B (OK)
1 1 0 0 1 1 -A-B< -2n-1
(underflow)
1 1 1 1 1 0 -A-B > -2n-1
(OK)
a,b are the MSBs of A and B. cin is carry in; cout=carry out

113. Overflow/Underflow Detection
 We find
1 1 , 1 1 1 , 1
n n in n n n in n
V a b c a b c
     
 

114. Overflow/Underflow Detection
, 1 , 1
in n out n
V c c
 
 
 You can also use
 That is, if for the MSB carry_in is
not equal to carry_out, overflow or
underflow has occurred.

115. TPS Quiz
19-20

116. Comparators

117. Equal Comparator
 Design a logic circuit which will
compute
F0 = (A = B)

118. 2-bit Equal Comparator Truth Table
b1 b0 a1 a0 F0
0 0 0 0 1
0 0 0 1 0
0 0 1 0 0
0 0 1 1 0
0 1 0 0 0
0 1 0 1 1
0 1 1 0 0
0 1 1 1 0

119. 2-bit Equal Comparator Truth Table
b1 b0 a1 a0 F0
1 0 0 0 0
1 0 0 1 0
1 0 1 0 1
1 0 1 1 0
1 1 0 0 0
1 1 0 1 0
1 1 1 0 0
1 1 1 1 1

120. Solution
  
0 1 1 0 0
F a b a b
  
You can show,

121. N-bit Equal Comparator
    
0 1 1 1 1 0 0
n n
F a b a b a b
 
   


122. Not Equal Comparator
 Design a logic circuit which will
compute
F = (A <> B)
F = (A = B)
i.e. Just invert our Equal Comparator circuit

123. Magnitude Comparator
 Design a logic circuit which will
compute
F2 = (A>B)
F1 = (A<B)
Let’s develop a truth table for 2-bits

124. 2-bit Magnitude (unsigned) Comparator
Truth Table
b1 b0 a1 a0 F2 F1
0 0 0 0 0 0
0 0 0 1 1 0
0 0 1 0 1 0
0 0 1 1 1 0
0 1 0 0 0 1
0 1 0 1 0 0
0 1 1 0 1 0
0 1 1 1 1 0

125. 2-bit Magnitude (unsigned) Comparator
Truth Table
b1 b0 a1 a0 F2 F1
1 0 0 0 0 1
1 0 0 1 0 1
1 0 1 0 0 0
1 0 1 1 1 0
1 1 0 0 0 1
1 1 0 1 0 1
1 1 1 0 0 1
1 1 1 1 0 0

126. You can show
2 1 1 0 1 0 1 0 0
F a b a b b a a b
  
1 1 1 1 0 0 0 1 0
F a b a a b a b b
  

127. TPS Quiz
21

128. Arithmetic Logic Units (ALUs)

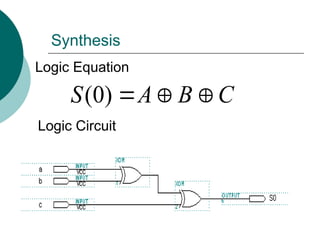
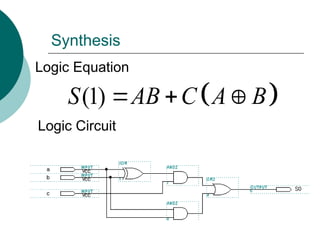
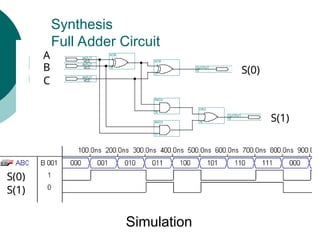
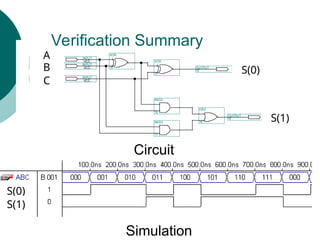
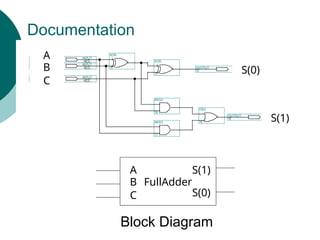
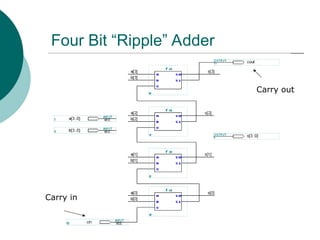
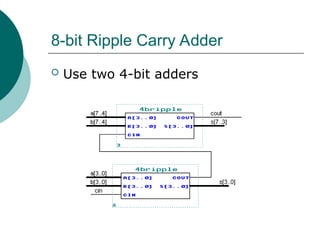
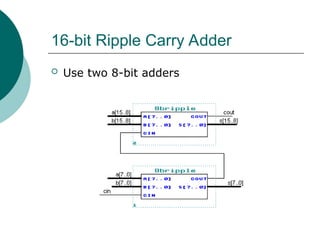
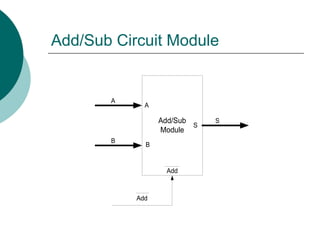
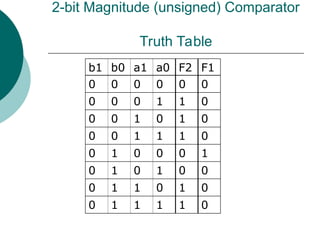
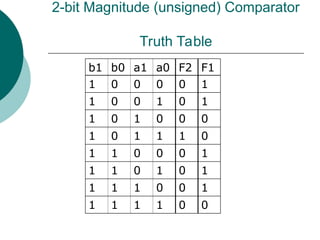
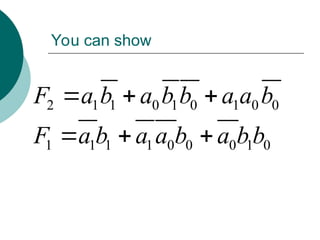
129. Arithmetic Logic Unit (ALU)
ALU
A[n-1,,0]
B[n-1..0]
F
S[m-1..0]
A,B are data inputs of n bits each in depth
S is a control input. We have 2m
operations
F is the output

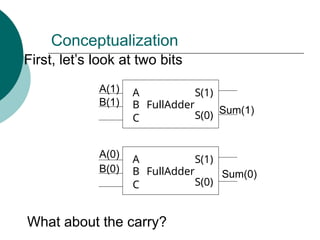
130. Example
 Let n=4,m=3
 We have A[3..0] and B[3..0]
 With m=3, we have 23
= 8 operations
 Let’s look at a possible function table

131. Function Table
s2 s1 s0 Function
0 0 0 F=AB
0 0 1 F=A+B (logical OR)
0 1 0 F=NOT A
0 1 1 F=A XOR B
1 0 0 F=A+B (Arithmetic)
1 0 1 F=A-B
1 1 0 F=A + 1
1 1 1 F=A - 1

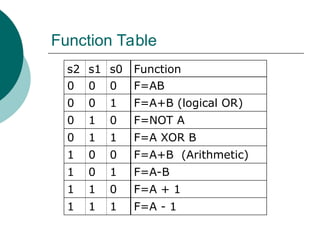
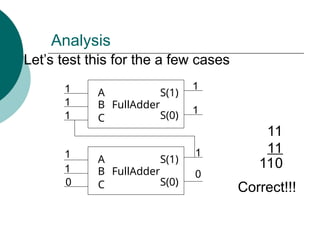
132. Design using a Truth Table
 How large is the truth table?
 2n from data inputs A and B
 Example: n=8, we have 16 data inputs
 A[7..0] and B[7..0]
 3 control inputs
 Total of 2n+3 inputs
 N=8, we have 19 inputs
 Our truth table will have
 192
(361) rows and 8 outputs
 Too complex. Let’s explore another
alternative using a “system” or modular
approach

133. Design using Modules
 Note:
 For S2=0, we have logic operations
 For S2=1, we have arithmetic
operations
 So, let’s use S2 to control a 2x1 MUX
 to select between logic and arithmetic
operations, so our top level design
would look like:

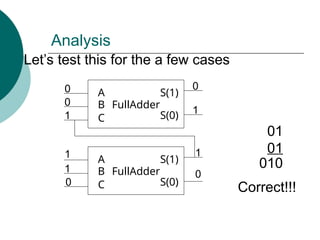
134. ALU Design
Logic
Module
Arithmetic
Module
2x1
MUX
S[2]
A B
A
A
B
F
A
B
F
S[1..0]
S[1..0]
B
F F

135. ALU Design S2=0
Logic
Module
Arithmetic
Module
2x1
MUX
S[2]
A B
A
A
B
F
A
B
F
S[1..0]
S[1..0]
B
F F
With S2=0, F is the output from
the logic module

136. ALU Design S2=1
Logic
Module
Arithmetic
Module
2x1
MUX
S[2]
A B
A
A
B
F
A
B
F
S[1..0]
S[1..0]
B
F F
With S2=1, F is the output from
the arithmetic module

137. Logic Module Design

138. Function Table for Logic Module
 S2=0
s2 s1 s0 Function
0 0 0 F=AB
0 0 1 F=A+B (logical OR)
0 1 0 F=NOT A
0 1 1 F=A XOR B
We can use a 4x1 mux to
implement this module

139. Logic Module Design
OR
NOT
XOR
AND
A
B
C
D
4
X
1
F
S[1..0]
S1 S0
A
A
B
F
A
B
F
A
B
F
A F
B

140. Logic Module Design
OR
NOT
XOR
AND
A
B
C
D
4
X
1
F
S[1..0]
S1 S0
A
A
B
F
A
B
F
A
B
F
A F
B
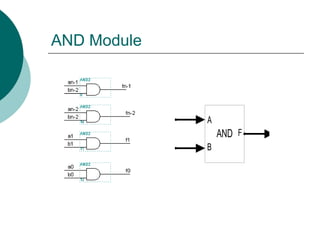
AND Operation
S[1..0]=00
0 0
F=AB

141. Logic Module Design
OR
NOT
XOR
AND
A
B
C
D
4
X
1
F
S[1..0]
S1 S0
A
A
B
F
A
B
F
A
B
F
A F
B
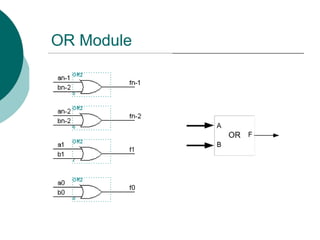
OR Operation
S[1..0]=01
0 1
F=A+B

142. Logic Module Design
OR
NOT
XOR
AND
A
B
C
D
4
X
1
F
S[1..0]
S1 S0
A
A
B
F
A
B
F
A
B
F
A F
B
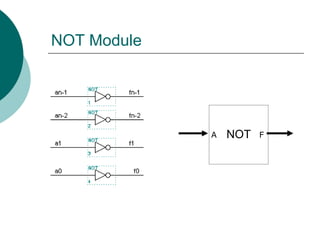
NOT Operation
S[1..0]=10
1 0
F=A

143. Logic Module Design
OR
NOT
XOR
AND
A
B
C
D
4
X
1
F
S[1..0]
S1 S0
A
A
B
F
A
B
F
A
B
F
A F
B
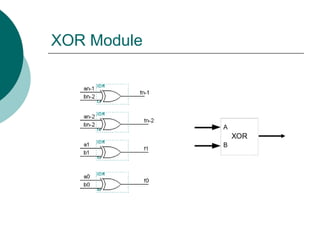
XOR Operation
S[1..0]=11
1 1
F=A XOR B

144. What do these logic modules
look like?

145. AND Module
AND
A
B
F

146. OR Module

147. NOT Module
NOT
A F

148. XOR Module

149. Arithmetic Module
Let’s use our ADD/SUB Module

150. Add/Sub Circuit Module
Add/Sub
Module
A
B
S
Add
A
B
Add
S

151. Function Table for Arithmetic Ops
s2 s1 s0 Function
1 0 0 F=A+B (Arithmetic)
1 0 1 F=A-B
1 1 0 F=A + 1
1 1 1 F=A - 1
Note:
S0 can be use to indicate Addition or Subtraction.
S1 can be use to indicate the B data input

152. Arithmetic Module Design
Add/Sub
Module
S0
A
B
Add
S
S
2
X
1
A
B
F
VDD
S1
B
A
S

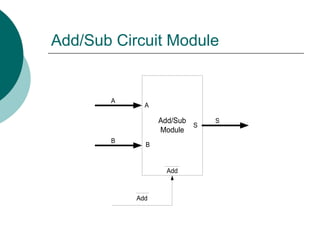
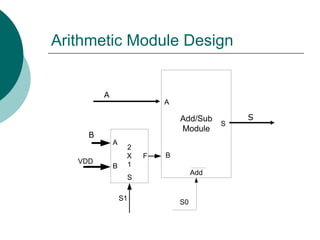
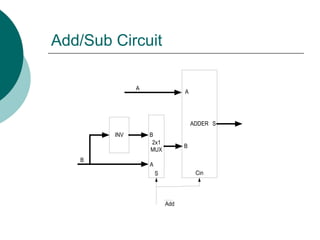
153. Arithmetic Module Design
Add/Sub
Module
S0
A
B
Add
S
S
2
X
1
A
B
F
VDD
S1
B
A
S
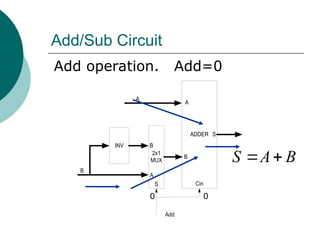
0
0
F=A+B
S[1..0]=00

154. Arithmetic Module Design
Add/Sub
Module
S0
A
B
Add
S
S
2
X
1
A
B
F
VDD
S1
B
A
S
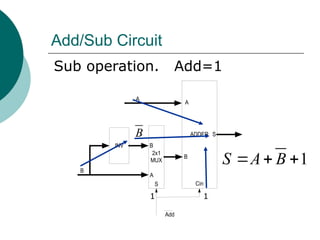
1
0
F=A-B
S[1..0]=01

155. Arithmetic Module Design
Add/Sub
Module
S0
A
B
Add
S
S
2
X
1
A
B
F
VDD
S1
B
A
S
0
1
F=A+1
S[1..0]=10

156. Arithmetic Module Design
Add/Sub
Module
S0
A
B
Add
S
S
2
X
1
A
B
F
VDD
S1
B
A
S
1
1
F=A-1
S[1..0]=11

157. Overall Design
We have

158. ALU Design
Logic
Module
Arithmetic
Module
2x1
MUX
S[2]
A B
A
A
B
F
A
B
F
S[1..0]
S[1..0]
B
F F

159. Logic Module Design
OR
NOT
XOR
AND
A
B
C
D
4
X
1
F
S[1..0]
S1 S0
A
A
B
F
A
B
F
A
B
F
A F
B

160. Arithmetic Module Design
Add/Sub
Module
S0
A
B
Add
S
S
2
X
1
A
B
F
VDD
S1
B
A
S

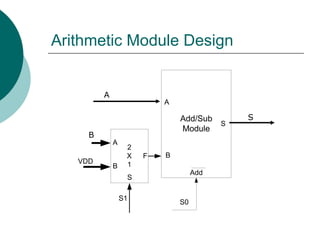
161. Total Design
OR
NOT
XOR
AND
A
B
C
D
4
X
1
F
S[1..0]
Add/Sub
Module
A
S
S0
A
B
Add
S
B
S
F
2
X
1
S2
S
2
X
1
A
B
F
VDD
S1 S0
S1
A B
A
B
F
A
B
F
A
B
F
A F
Logic Module
Arithmetic Module

162. End of Chapter 4