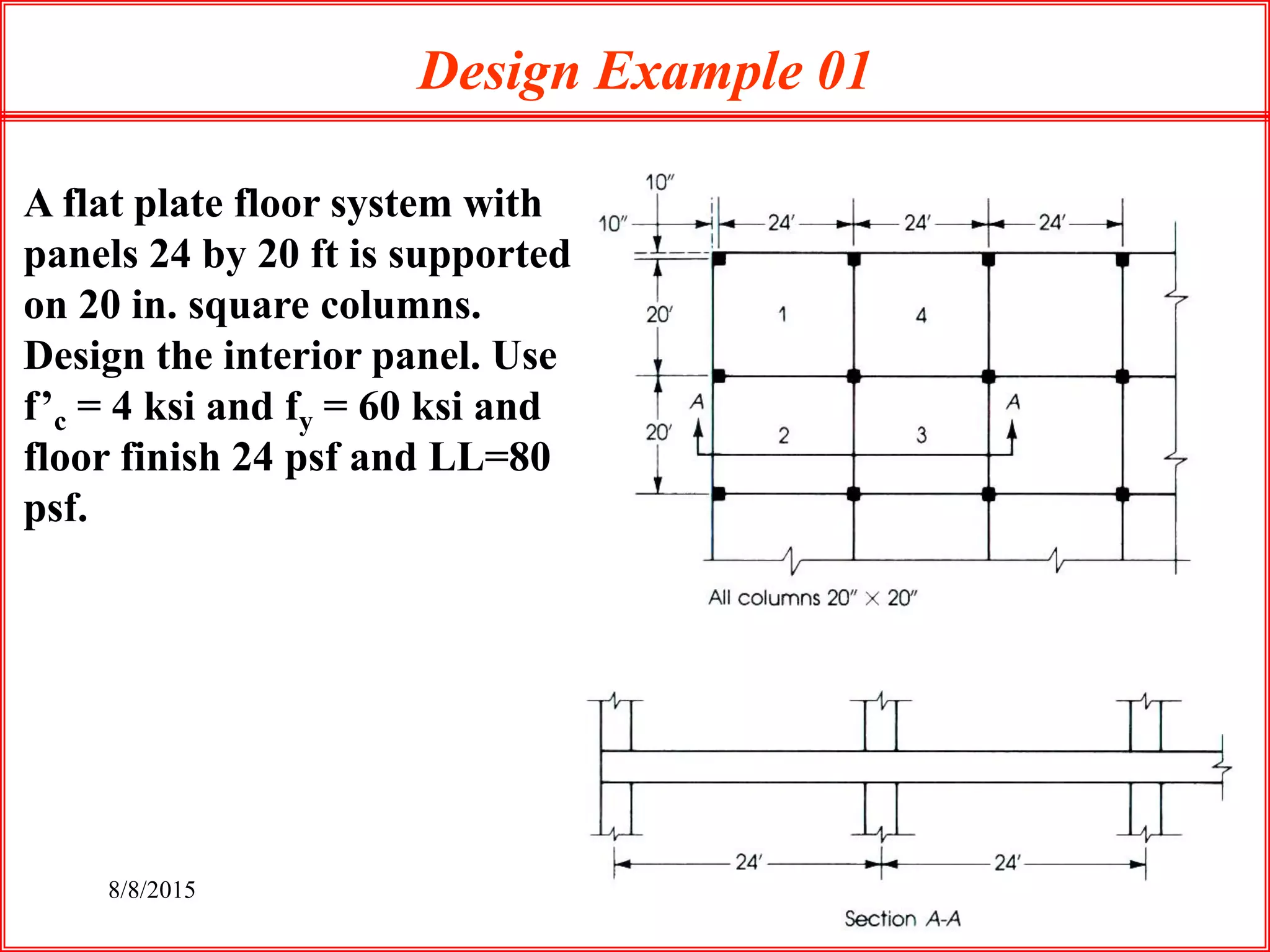
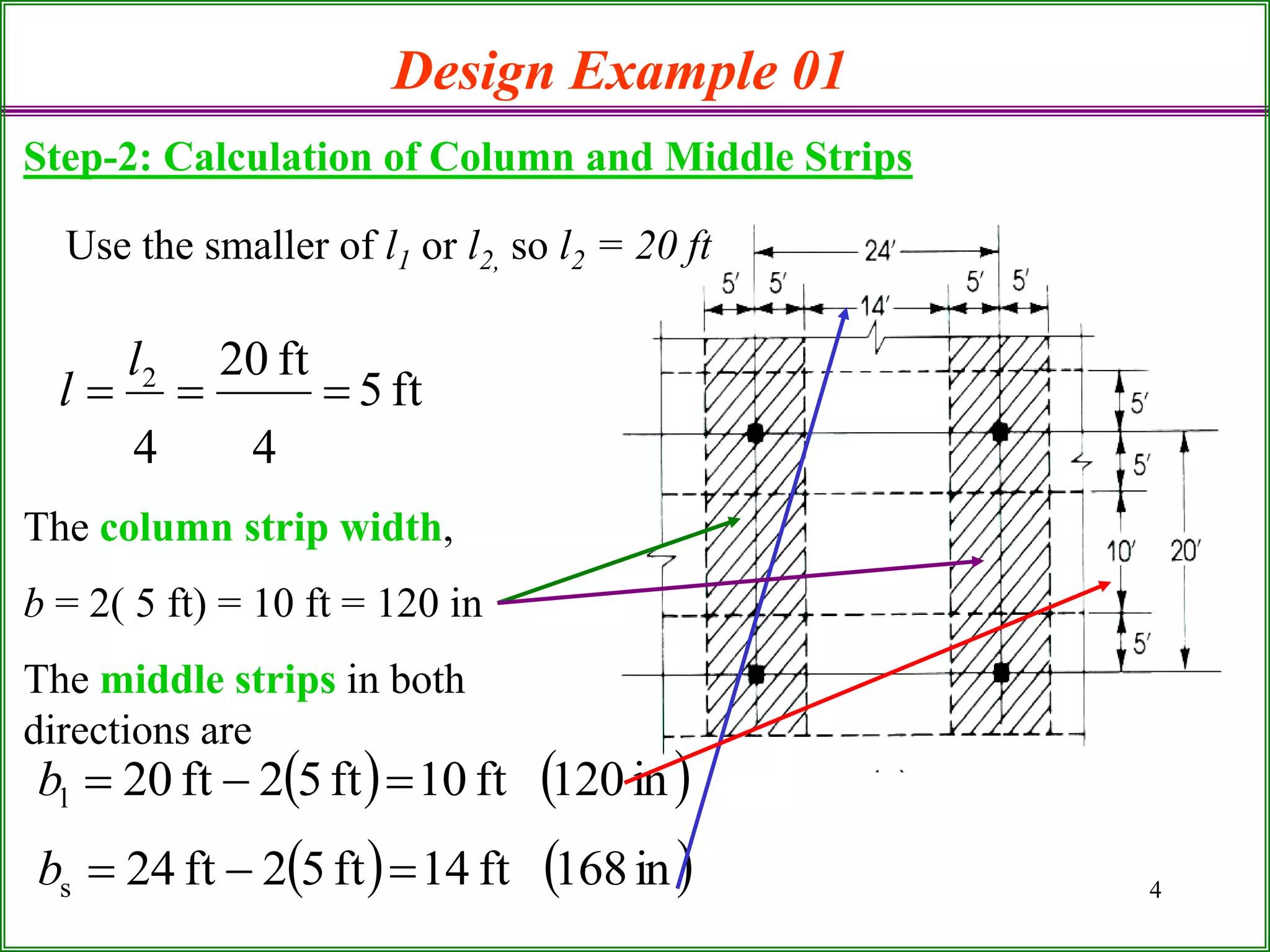
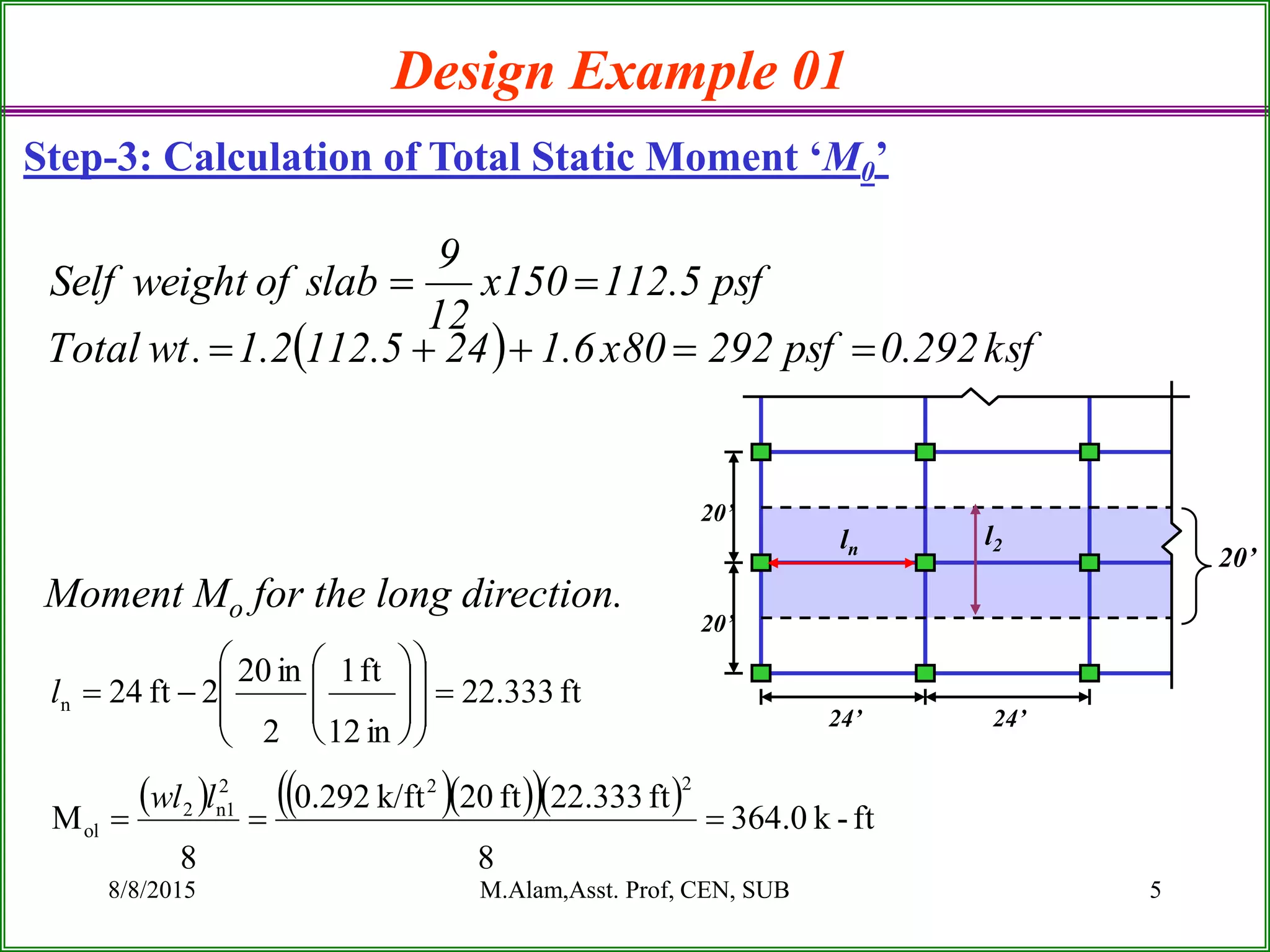
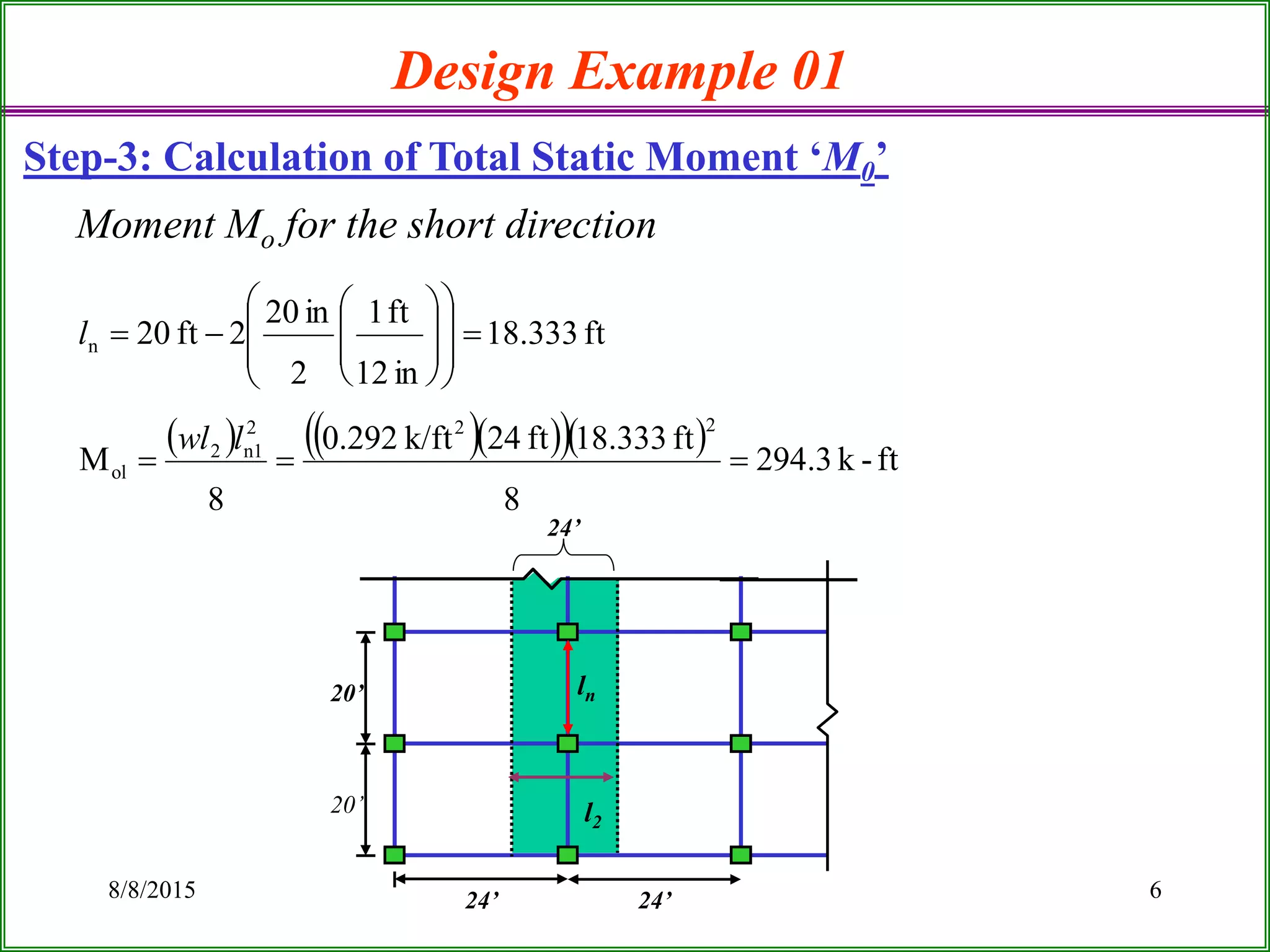
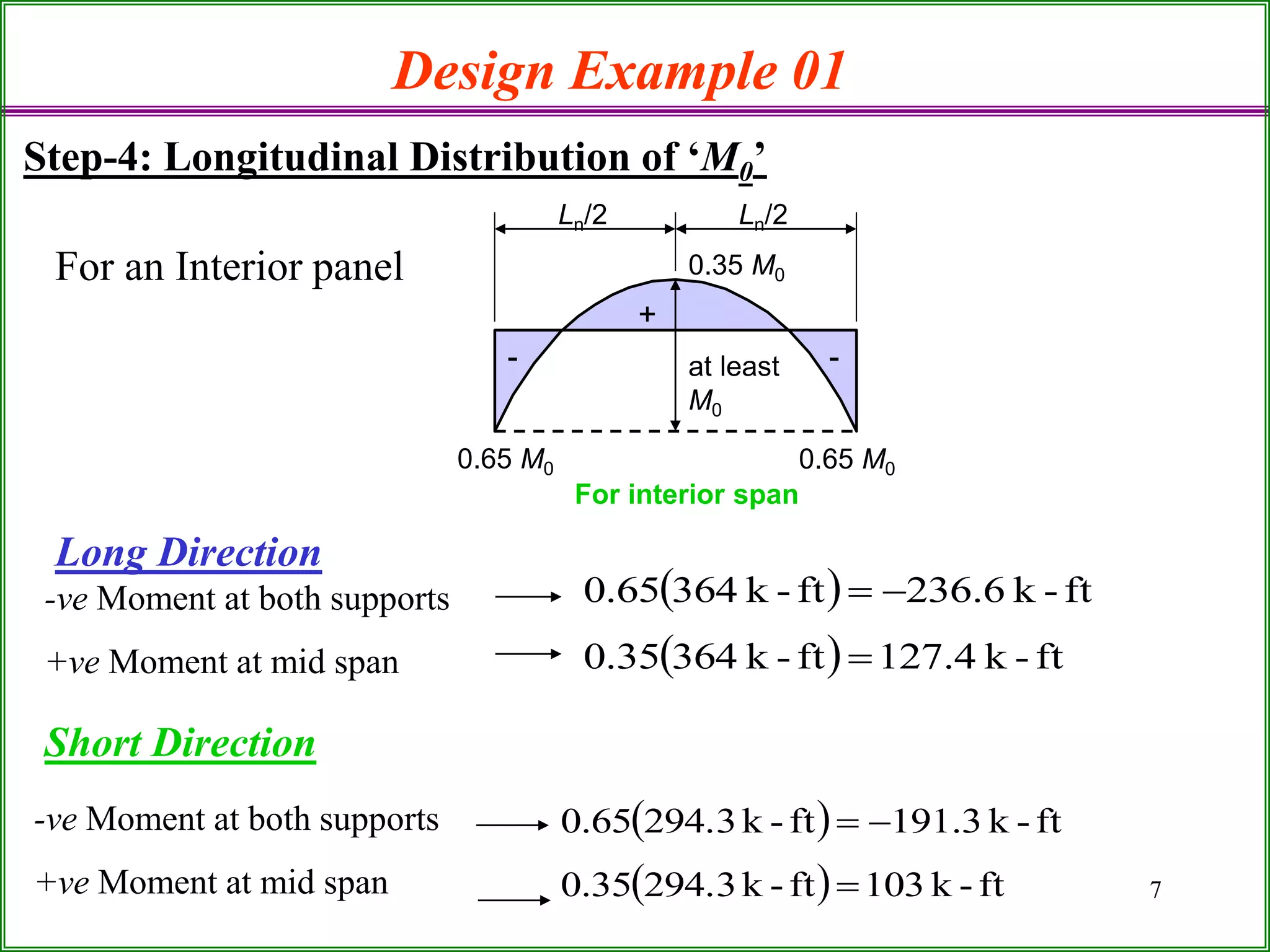
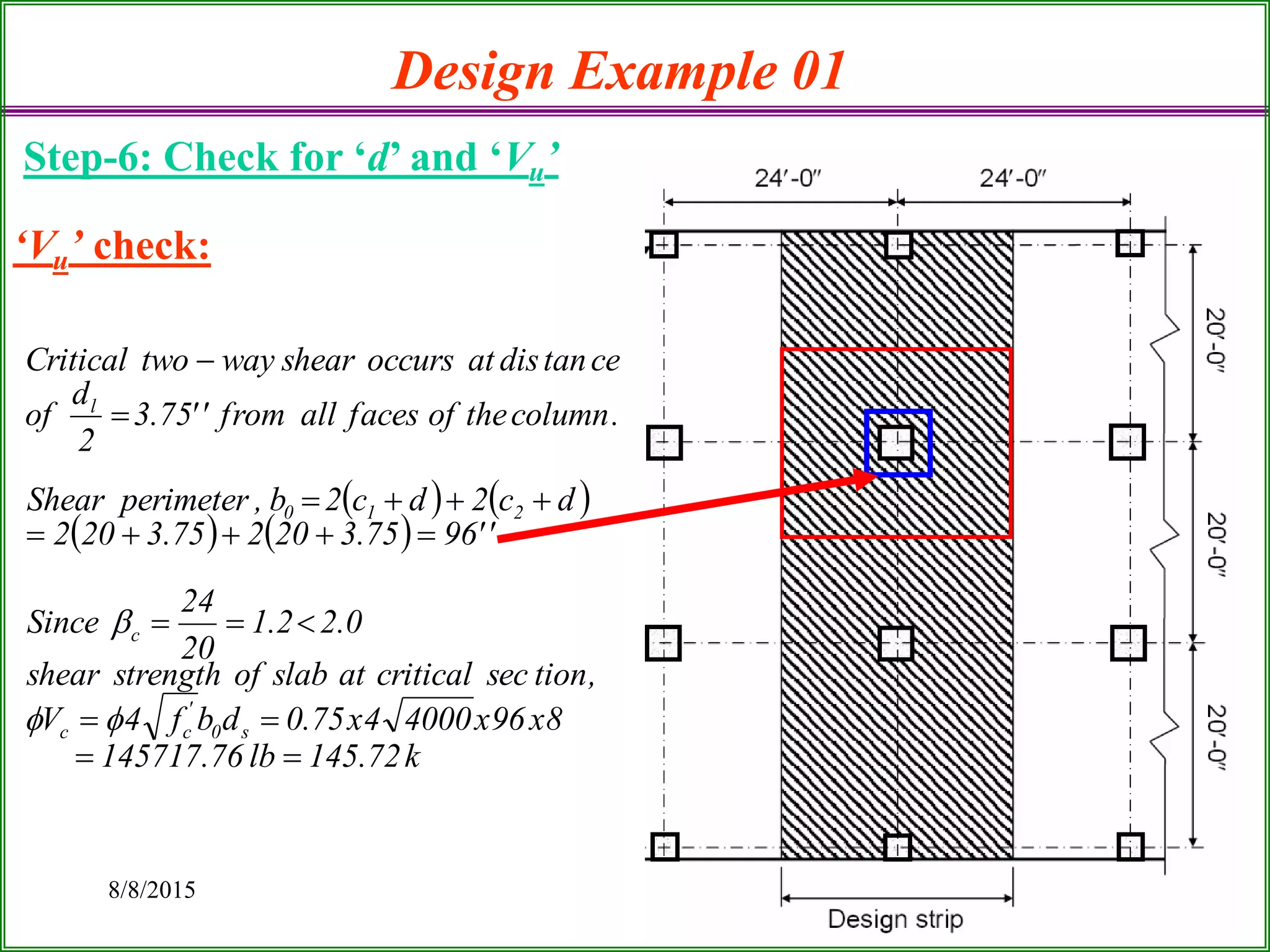
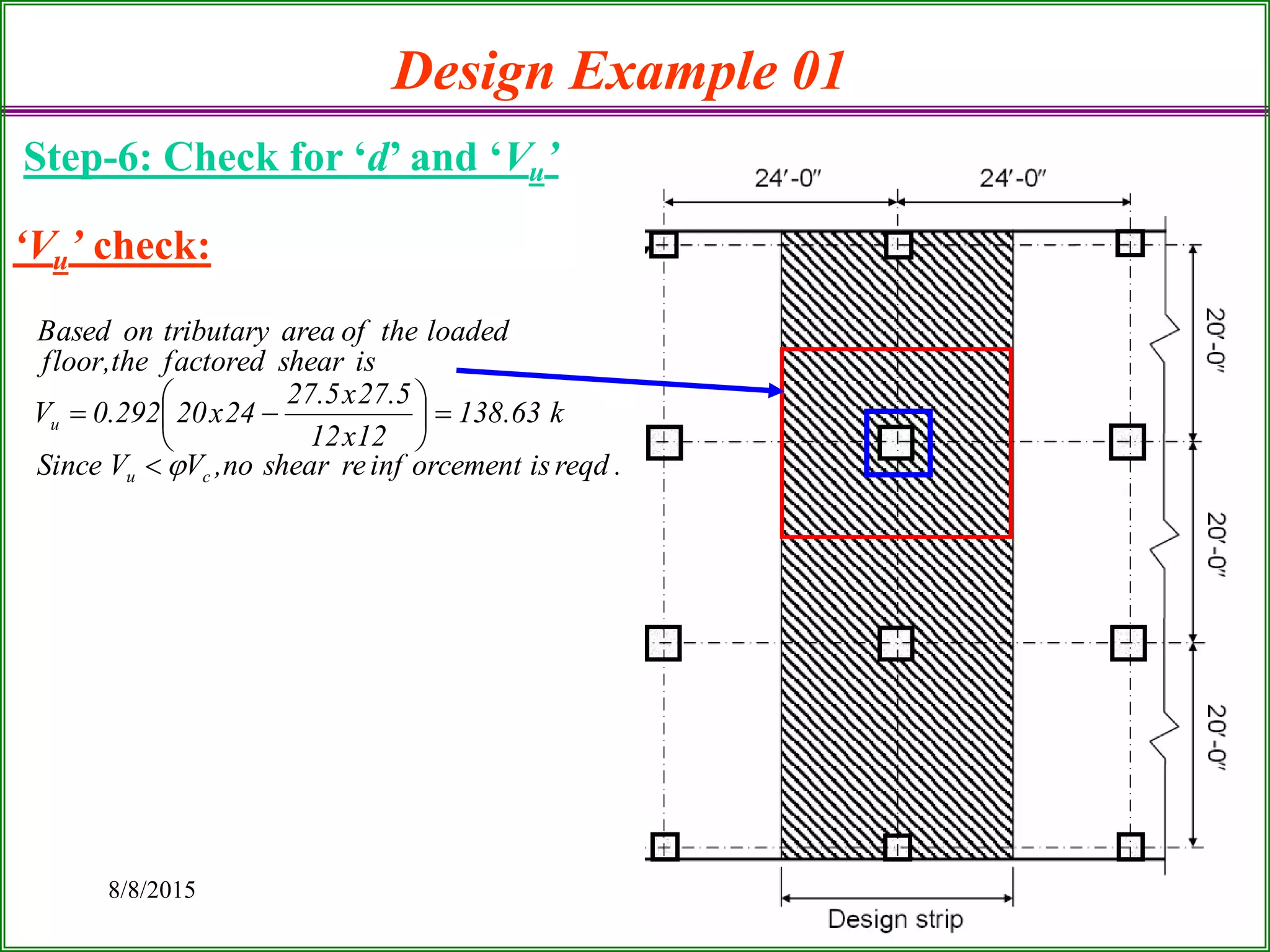
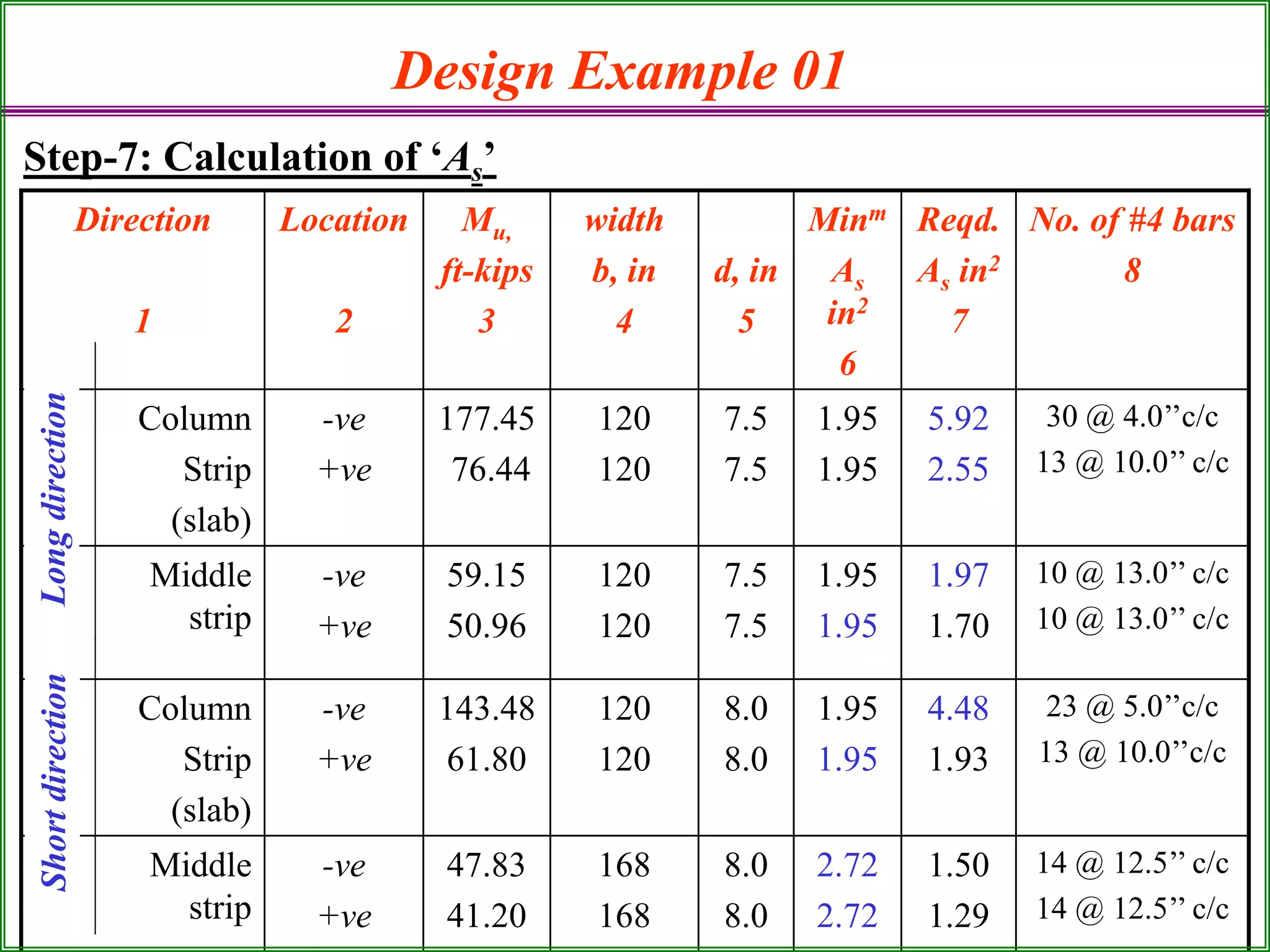
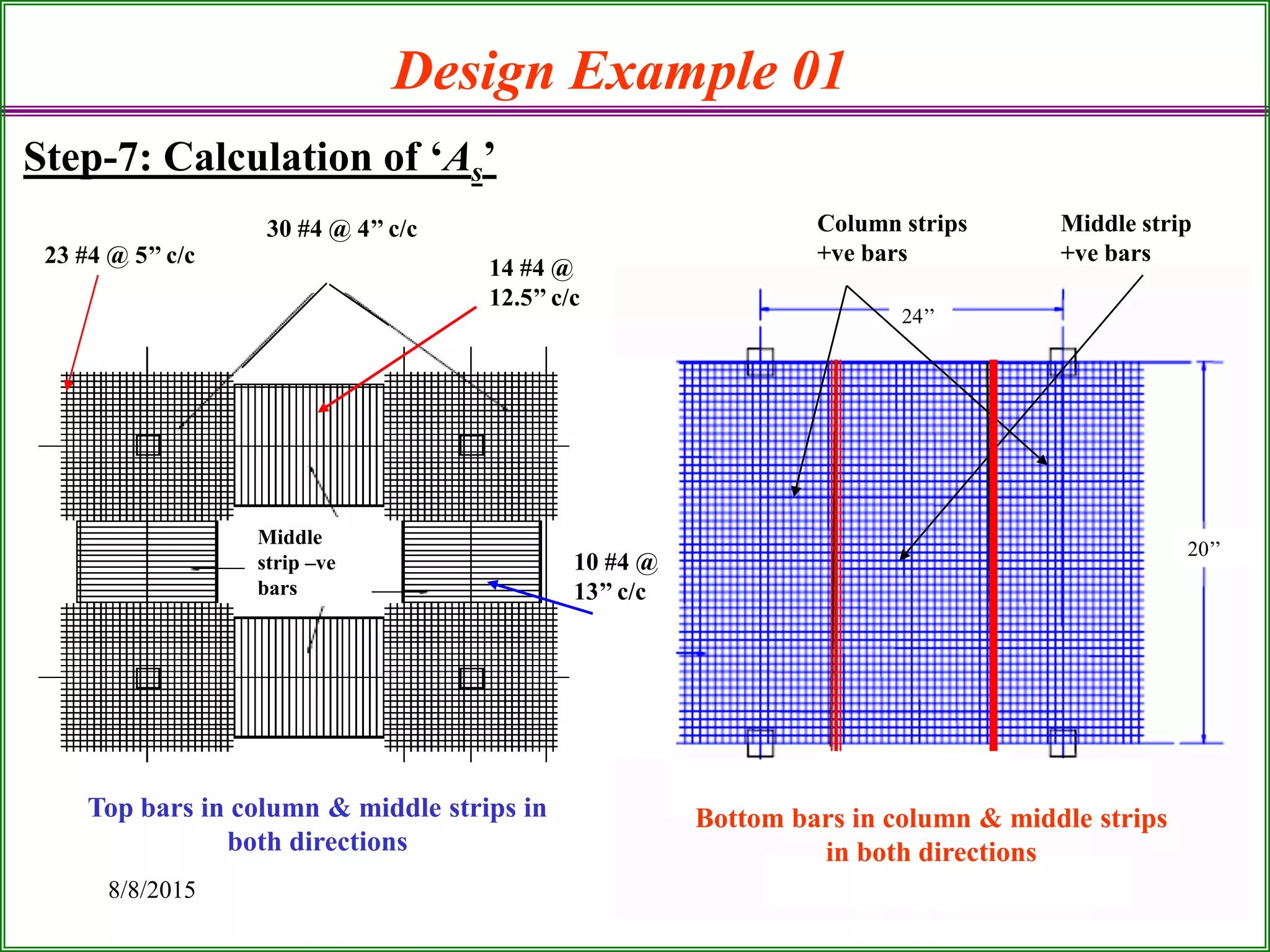
The document outlines the design process for a flat plate slab floor system supported by columns, detailing calculations for slab thickness, moment distribution, and reinforcement requirements. Key steps include determining effective slab depths, static moments for both long and short spans, and checks for shear and reinforcement areas. The design example uses specific material strengths and loads to arrive at necessary dimensions and reinforcement detailing.

1. LECTURE 3
DESIGN PROBLEM OF FLAT PLATE SLAB
By
MD. MAHBUB-UL-ALAM
ASST. PROF, DEPT. OF CIVIL ENGG.
Stamford University Bangladesh

2. 8/8/2015 2
Design Example 01
A flat plate floor system with
panels 24 by 20 ft is supported
on 20 in. square columns.
Design the interior panel. Use
f’c = 4 ksi and fy = 60 ksi and
floor finish 24 psf and LL=80
psf.

3. 8/8/2015 M.Alam,Asst. Prof, CEN, SUB 3
Step 1: Calculation of Minimum Thickness ‘h’
Design Example 01
Slab thickness of an interior panel for fy = 60 ksi and no edge beams,
Effective depths, ds = 9.0-1.0 = 8.0 inch
dl = 9.0-1.5 = 7.5 inch
''0.9''12.8
33
2012x24
33
l
h n




4. 4
Design Example 01
Step-2: Calculation of Column and Middle Strips
Use the smaller of l1 or l2, so l2 = 20 ft
ft5
4
ft20
4
2

l
l
The column strip width,
b = 2( 5 ft) = 10 ft = 120 in
The middle strips in both
directions are
   
   in168ft14ft52ft24
in120ft10ft52ft20
s
l


b
b

5. 8/8/2015 M.Alam,Asst. Prof, CEN, SUB 5
Design Example 01
Step-3: Calculation of Total Static Moment ‘M0’
  ksf292.0psf29280x6.1245.1122.1.wtTotal
psf5.112150x
12
9
slabofweightSelf


Moment Mo for the long direction.
       ft-k0.364
8
ft333.22ft20k/ft292.0
8
M
ft333.22
in12
ft1
2
in20
2ft24
222
n12
ol
n



















lwl
l
24’ 24’
20’
20’
20’
l2ln

6. 8/8/2015 6
Design Example 01
Step-3: Calculation of Total Static Moment ‘M0’
Moment Mo for the short direction
       ft-k3.294
8
ft333.18ft24k/ft292.0
8
M
ft333.18
in12
ft1
2
in20
2ft20
222
n12
ol
n



















lwl
l
24’ 24’
20’
20’
24’
l2
ln

7. 7
Design Example 01
Step-4: Longitudinal Distribution of ‘M0’
For an Interior panel
For interior span
0.35 M0
Ln/2 Ln/2
0.65 M0 0.65 M0
at least
M0
+
- -
 
  ft-k4.127ft-k36435.0
ft-k6.236ft-k64365.0

-ve Moment at both supports
+ve Moment at mid span
Long Direction
-ve Moment at both supports
+ve Moment at mid span
 
  ft-k103ft-k94.3235.0
ft-k3.191ft-k94.3265.0


Short Direction

8. 8/8/2015 M.Alam,Asst. Prof, CEN, SUB 8
Design Example 01
Step-5: Transverse Distribution of ‘M0’
Long Direction
These distributions depend on the ratio of length l2/l1 and α1 l2/l1
0
l
l
8333.0
24
20
l
l
0
1
2
1
1
2
1






9. 8/8/2015 M.Alam,Asst. Prof, CEN, SUB 9
Design Example 01
Step-5: Transverse Distribution of ‘M0’
Long Direction
Distribution % of –ve and +ve moments into column strips are as below:
Factor = 0.75 Factor = 0.60

10. 8/8/2015 M.Alam,Asst. Prof, CEN, SUB 10
Column Strip
Middle Strip
Design Example 01
Step-5: Transverse Distribution of ‘M0’
Long Direction
ftk44.764.127x60.0momentve
ftk45.1776.236x75.0momentve


ftk96.504.127x40.0momentve
ftk15.596.236x25.0momentve



11. 8/8/2015 M.Alam,Asst. Prof, CEN, SUB 11
Design Example 01
Step-5: Transverse Distribution of ‘M0’
Short Direction
These distributions also depend on the ratio of length l2/l1 and α1 l2/l1
0
l
l
222.1
20
24
l
l
0
1
2
1
1
2
1






12. 8/8/2015 M.Alam,Asst. Prof, CEN, SUB 12
Design Example 01
Step-5: Transverse Distribution of ‘M0’
Short Direction
Distribution % of –ve and +ve moments into column strips are as below:
Factor = 0.75 Factor = 0.60

13. 8/8/2015 M.Alam,Asst. Prof, CEN, SUB 13
Column Strip
Middle Strip
Design Example 01
Step-5: Transverse Distribution of ‘M0’
Short Direction
ftk80.610.103x60.0momentve
ftk48.1433.191x75.0momentve


ftk20.410.103x40.0momentve
ftk83.473.191x25.0momentve



14. 8/8/2015 M.Alam,Asst. Prof, CEN, SUB 14
Design Example 01
Step-6: Check for ‘d’ and ‘Vu’
ok''0.8''39.3d
4
60x0214.0
59.01xd168x60x0214.0x90.012x48.143
''0.8d,''168b,ftk6.48.143moment.maxdirectionshortIn
ok''5.7''35.4d
4
60x0214.0
59.01xd120x60x0214.0x90.012x45.177
MM,Now
0214.0,Let
''5.7d,''120b,ftk45.177moment.maxdirectionlongIn
2
p
2
nu
max
p



















‘d’ check:

15. 8/8/2015 15
Design Example 01
Step-6: Check for ‘d’ and ‘Vu’
‘Vu’ check:
   
   
k72.145lb76.145717
8x96x40004x75.0dbf4V
,tionseccriticalatslabofstrengthshear
0.22.1
20
24
Since
''9675.320275.3202
dc2dc2b,perimeterShear
.columntheoffacesallfrom''75.3
2
d
of
cetandisatoccursshearwaytwoCritical
s0
'
cc
c
210
l










16. 8/8/2015 16
Design Example 01
Step-6: Check for ‘d’ and ‘Vu’
.reqdisorcementinfreshearno,VVSince
k63.138
12x12
5.27x5.27
24x20292.0V
isshearfactoredthe,floor
loadedtheofareatributaryonBased
cu
u








‘Vu’ check:

17. Design Example 01
Step-7: Calculation of ‘As’
Direction
1
Location
2
Mu,
ft-kips
3
width
b, in
4
d, in
5
Minm
As
in2
6
Reqd.
As in2
7
No. of #4 bars
8
Column
Strip
(slab)
-ve
+ve
177.45
76.44
120
120
7.5
7.5
1.95
1.95
5.92
2.55
30 @ 4.0’’c/c
13 @ 10.0’’ c/c
Middle
strip
-ve
+ve
59.15
50.96
120
120
7.5
7.5
1.95
1.95
1.97
1.70
10 @ 13.0’’ c/c
10 @ 13.0’’ c/c
Column
Strip
(slab)
-ve
+ve
143.48
61.80
120
120
8.0
8.0
1.95
1.95
4.48
1.93
23 @ 5.0’’c/c
13 @ 10.0’’c/c
Middle
strip
-ve
+ve
47.83
41.20
168
168
8.0
8.0
2.72
2.72
1.50
1.29
14 @ 12.5’’ c/c
14 @ 12.5’’ c/c
LongdirectionShortdirection

18. 8/8/2015 18
Design Example 01
Step-7: Calculation of ‘As’
30 #4 @ 4’’ c/c
24’’
20’’
Middle
strip –ve
bars
Top bars in column & middle strips in
both directions
Bottom bars in column & middle strips
in both directions
Column strips
+ve bars
Middle strip
+ve bars23 #4 @ 5’’ c/c
10 #4 @
13’’ c/c
14 #4 @
12.5’’ c/c

19. 8/8/2015 19
Design Example 01
Step-7: Calculation of ‘As’
b
s
u
'
cy
u
s
s
A
A
barselectedoneofArea
areassteelrequiredTotal
barstotalof.no'n'where
inch18or'h2'
1n
stripofWidth
s,Spacing
trequiremensteelimummin)2
.lessiswhicheverinch18or'h2'spacingimummax)1
gconsiderincalculatedisbarsof.No
:8#Column
inchin'd'andkftinMomentMwhere
ksi4f&ksi60fwhenonly,
d4
M
A,steelrequiredTotal
:7#Column
stripmiddleorcolumnofwidthbwhere,bh0018.0AMinimum
:6#Column






