The document discusses lateral load resisting systems in high-rise concrete buildings, detailing types such as moment-resisting frames and shear walls, as well as their combinations. It covers key concepts including the definition of the center of rigidity, methods for distributing lateral loads, and the evaluation of structural stability through critical parameters. Practical examples illustrate calculations for effective inertia and load distribution among various structural frames.

1. Lateral load Resisting Systems
Dr. Ahmed Tarabia
High rise concrete building, 3rd Civil
Spring 2015

2. ‫الجانبية‬ ‫لالحمال‬ ‫المقاومة‬ ‫االنظمة‬ ‫انواع‬
•‫المقاومة‬ ‫االطارات‬‫للعزوم‬:
‫الكمرات‬ ‫و‬ ‫األعمدة‬ ‫من‬ ‫تتكون‬‫الخرسانية‬.
•‫حوائط‬‫الحوائط‬ ‫أو‬ ‫القص‬‫االنشائية‬.
•‫المركبة‬ ‫االنظمة‬:
‫االطارات‬ ‫من‬ ‫مجموعة‬ ‫من‬ ‫تتكون‬+‫القص‬ ‫حوائط‬.

3. OBJECTIVES
• 1- Rigidity center definition, how to locate it?
• 2- Lateral Load Resisting Systems In Each Direction.
• 3-How To Distribute Lateral Loads Between Lateral
Load Resisting Systems In Each Lateral Direction.
(Relative rigidity method)

4. General rules
• A system or more should be provided in each
direction of the principal directions.
• These systems should be able to resist the
lateral loads.
Check: (Drift-moment-Shear-Stability)

5. Moment resisting frames

6. Moment resisting frames

7. Shear wall system

8. Shear wall system
   

9. Dual system:(Shear walls + Frames)

10. ‫الجساءة‬ ‫مركز‬Center of Rigidity
•‫المستوي‬ ‫في‬ ‫جسئ‬ ‫كسطح‬ ‫تتحرك‬ ‫دور‬ ‫كل‬ ‫بالطة‬ ‫أن‬ ‫افتراض‬
•‫مركز‬‫أثر‬ ‫اذا‬ ‫الدور‬ ‫مستوى‬ ‫فى‬ ‫افتراضية‬ ‫نقطة‬ ‫هو‬ ‫الجساءة‬
‫انتقالية‬ ‫حركة‬ ‫جسئ‬ ‫كجسم‬ ‫المستوي‬ ‫يتحرك‬ ‫فيها‬ ‫الجانبية‬ ‫القوة‬
‫المؤثرة‬ ‫القوة‬ ‫اتجاه‬ ‫في‬‫بدون‬‫حدوث‬‫دوران‬.
•‫انتقالية‬ ‫حركة‬ ‫يحدث‬ ‫آخر‬ ‫مكان‬ ‫اي‬ ‫في‬ ‫القوة‬ ‫أثرت‬ ‫اذا‬ ‫و‬
‫التواء‬ ‫عزم‬ ‫لوجود‬ ‫نتيجة‬ ‫دوران‬ ‫حدوث‬ ‫مع‬ ‫للمستوي‬.

11. ‫األولي‬ ‫الحالة‬:‫الجساءة‬ ‫مركز‬ ‫في‬ ‫تؤثر‬ ‫القوة‬

12. ‫الثانية‬ ‫الحالة‬:‫الجساءة‬ ‫مركز‬ ‫خارج‬ ‫تؤثر‬ ‫القوة‬

13. ‫الجساءة‬ ‫مركز‬ ‫تحديد‬Xo , Yo
•‫اتجاه‬ ‫لكل‬ ‫المقاومة‬ ‫عناصر‬ ‫تحديد‬ ‫يتم‬.
•‫حساب‬ ‫يتم‬Ieffective‫ألخذ‬‫بالقطاعات‬ ‫التشريخ‬ ‫تاثير‬‫الخرسانية‬:
How to find the inertia of the lateral resisting system
•‫محور‬ ‫حول‬ ‫الجساءات‬ ‫عزوم‬ ‫باستخدام‬ ‫الجساءة‬ ‫مركز‬ ‫تحديد‬ ‫يتم‬X &Y
‫اآلتية‬ ‫المعادالت‬ ‫طريق‬ ‫عن‬ ‫مكان‬ ‫أس‬ ‫في‬ ‫فرضهم‬ ‫يتم‬ ‫و‬:

14. ‫محور‬ ‫حول‬ ‫الجساءات‬ ‫عزوم‬ ‫باستخدام‬X &Y‫اآلتية‬ ‫المعادالت‬ ‫طريق‬ ‫عن‬:
‫محور‬ ‫اتجاه‬ ‫في‬ ‫الجانبية‬ ‫المقاومة‬ ‫لعناصر‬X:
‫محور‬ ‫اتجاه‬ ‫في‬ ‫الجانبية‬ ‫المقاومة‬ ‫لعناصر‬Y:
nx Number of lateral load resisting systems in X direction
ny Number of lateral load resisting systems in X direction

15. Y
C.R.Xo
Yo

16. Simple examples: #1

17. Simple examples: #2

18. In the case of symmetry of lateral load resisting system
Ey=0.0
Force 3C
C.R.
1C1C C2
Y
X
A B C
1
2
3 3
2
1
CBA
B12C 2C
2CC1 C1

19. Step 2:
• Transfer axes systems to the rigidity center.
Y
C.R.

20. Distribution of lateral forces
•-‫الجانبية‬ ‫القوة‬ ‫حالة‬ ‫في‬FY‫اتجاه‬ ‫في‬Y:
• For each Y-direction resisting elements:
• For each X-direction resisting elements:
)y*(I)x*(I
.XI
.eF
I
I
F=F
2
j
1
yj
2
j
1
xj
ixi
xy
1
xj
xi
yyi



 nx
j
ny
j
ny
j
)y*(I)x*(I
.yI
.eF=F
2
j
1
yj
2
j
1
xj
iyi
xyxi



 nx
j
ny
j

21. -‫الجانبية‬ ‫القوة‬ ‫حالة‬ ‫في‬FY‫اتجاه‬ ‫في‬Y:
Then, For Y-direction resisting elements:


ny
1j
xj
xi
yyi
I
I
.F=F
0.0eif y 

22. •-‫الجانبية‬ ‫القوة‬ ‫حالة‬ ‫في‬F x‫اتجاه‬ ‫في‬X:
• For X-direction resisting elements:
• For Y-direction resisting elements:
)y*(I)x*(I
.YI
.eF
I
I
F=F
2
j
1
yj
2
j
1
xj
iyi
yx
1
yj
yi
xxi



 nx
j
ny
j
nx
j
)y*(I)x*(I
.xI
.eF=F
2
j
1
yj
2
j
1
xj
ixi
yxyi



 nx
j
ny
j

23. -‫الجانبية‬ ‫القوة‬ ‫حالة‬ ‫في‬F x‫اتجاه‬ ‫في‬:X
For X-direction resisting elements:


nx
j
yj
1
yi
xxi
I
I
.F=F
0.0eif x


24. Example #1
Force 3C
C.R.
1C1C C2
Y
X
A B C
1
2
3 3
2
1
CBA
B12C 2C
2CC1 C1

25. Lateral load resisting systems
• X ‫اتجاه‬ ‫في‬ ‫الجانبية‬ ‫األحمال‬ ‫لمقاومة‬ ‫االنشائي‬ ‫النظام‬
• a- The frames on axis (1-1), (2-2) and (3-3).
• Y ‫اتجاه‬ ‫فى‬ ‫االنشائي‬ ‫النظام‬ ‫يتكون‬ ‫و‬
• a- The frames on axis (A-A), (B-B) and (C-C).
• ‫تأثير‬ ‫نتيجة‬ ‫االنشائية‬ ‫العناصر‬ ‫جميع‬ ‫نصيب‬ ‫احسب‬‫الحمل‬ ‫هذا‬.

26. The sections of C1 600mm x800mm
The sections of C2 800mm x1000mm and
The section of C3 is 1000mm x 1000mm.
4
3
y:1 0179.0
12
0.8x0.6
x0.7ICfor m
Find effective inertia-1
4
3
y 0467.0
12
1.0x0.8
x0.7I:C2For m
4
3
y3 0583.0
12
1.0x1.0
x0.7I:CFor m

27. 2-Find the Centre of Rigidity:
Because the lateral load resisting systems
are symmetric in X and Y directions, the
center of rigidity is located in the center of
the two systems.
- Transfer axes system to the center of rigidity

28. 1C
A
3
Fx
2
2C
1
A
C1
X
3
2
1
23C
C.R.
C2
Y
B
B
B1
2C
1C
C
C
C
C1

29. 3 - Load distribution:
In this example, a load in X-direction =Fx is acting at the mid-point of the floor.
We need to find the share of each resisting system of this load
using the following equations. Because ey=0.0, then:
"For X-dir. resisting element"


nx
j 1
yj
yi
xxi
I
I
F=F

30. System in Section Iy Yi
Fx Fx/frame
X-direction (m x m) (m4) (m)
Frame (1-1)
.8*.6 0.0179 3 0.05652
0.2601.0*0.80
0.0467
3 0.147458
.8*.6 0.0179 3 0.05652
Frame (2-2)
1.0*0.80
0.0467
0 0.147458
0.481.0*1.0
0.0583
0 0.184086
1.0*0.80
0.0467
0 0.147458
Frame (3-3)
.8*.6 0.0179 -3 0.05652
0.2601.0*0.80
0.0467
-3 0.147458
.8*.6 0.0179 -3 0.05652
SUM 0.3167 1 1

31. Distribution of lateral loads on frames

32. Frame#3
Frame #2
Frame #1
C1 1C1C
C2C2 B1
A B C
1
2
33
2
1
CBA
X
Y
2CC1 C1
C3Fx
Frame#4
Example #2

33. Data of the problem:
The sections of C1 600mm x800mm
The sections of C2 800mm x1000mm and
The section of C3 1000mm x 1000mm.
X ‫اتجاه‬ ‫في‬ ‫الجانبية‬ ‫األحمال‬ ‫لمقاومة‬ ‫االنشائي‬ ‫النظام‬
a- The frames on axis (2-2) and (3-3).
Y ‫اتجاه‬ ‫فى‬ ‫االنشائي‬ ‫النظام‬ ‫يتكون‬ ‫و‬
a- The frames on axis (A-A), and (C-C).
FX kN ‫تأث‬ ‫نتيجة‬ ‫االنشائية‬ ‫العناصر‬ ‫جميع‬ ‫نصيب‬ ‫احسب‬‫الحمل‬ ‫هذا‬ ‫ير‬.

34. Find effective inertia-1
4
3
x
:
4
3
y:1
010.0
12
0.6x0.8
x0.7I
0179.0
12
0.8x0.6
x0.7ICfor
m
m


4
3
x
4
3
y
029.0
12
0.8x1.0
x0.7I
0467.0
12
1.0x0.8
x0.7I:C2For
m
m


4
3
x
4
3
y3
0583.0
12
1.0x1.0
x0.7I
0583.0
12
1.0x1.0
x0.7I:CFor
m
m



35. Frame #2
Frame #1
C2C2 B1
X
Y
2CC1 C1
C3Force
Frame#4
Frame#3
1C1C
C2C2
X
Y
C1 C1
Fx
X ‫اتجاه‬ ‫في‬ ‫الجانبية‬ ‫األحمال‬ ‫لمقاومة‬ ‫االنشائي‬ ‫النظام‬ Y‫اتجاه‬ ‫في‬ ‫الجانبية‬ ‫األحمال‬ ‫لمقاومة‬ ‫االنشائي‬ ‫النظام‬

36. Find the Centre of Rigidity:-2
System in
Col.
Section
Ix Xi
Ix . Xi
Y-direction (m x m) (m4) (m)
Frame (A-A)
0.8x0.60 0.01 0 0
1.0x0.80 0.03 0 0
0.8x0.60 0.0583 0 0
Frame (C-C)
0.8x0.60 0.01 6 0.06
1.0x0.80 0.03 6 0.18
0.8x0.60 0.0583 6 0.3498
SUM 0.1966 0.5898
A- Find Xo
m
I
XI
y
y
n
i
ix
n
i
ixi
0.3
1966.0
5898.
=X
1
1
o 




Assume that the X axis is axis (3-3) and the Y axis is axis (A-A)

37. System in
Col.
Section
Iy Yi
Iy . Yi
X-direction (m x m) (m4) (m)
Frame (1-1)
0.8x0.60 0.0179 0 0
1.0x0.80 0.0467 0 0
0.8x0.60 0.0179 0 0
Frame (2-2)
1.0x0.80 0.0467 3 0.1401
1.0x1.00 0.0583 3 0.1749
1.0x0.80 0.0467 3 0.1401
SUM 0.2342 0.4551
m
I
YI
x
x
n
i
yi
n
i
iyi
1.94
233.0
455.0
=Y
1
1
o 




B- Find Yo

38. 3C
1C1C C2
B12C 2C
C1 C11C
Frame #1
Frame #2Frame#3
Frame#3
C.R.
Force
Y
X
ex=0.0 and ey = 3.0 – 1.94 = 1.06 m
- M = Fx . ey = Fx . (1.06)

39. •-‫اتجاه‬ ‫في‬ ‫الجانبية‬ ‫القوة‬ ‫حالة‬ ‫في‬X‫و‬F x
• For X-direction resisting elements:
• For Y-direction resisting elements:
)y*(I)x*(I
.YI
.eF
I
I
F=F
2
j
1
yj
2
j
1
xj
iyi
yx
1
yj
yi
xxi



 nx
j
ny
j
nx
j
)y*(I)x*(I
.xI
.eF=F
2
j
1
yj
2
j
1
xj
ixi
yxyi



 nx
j
ny
j

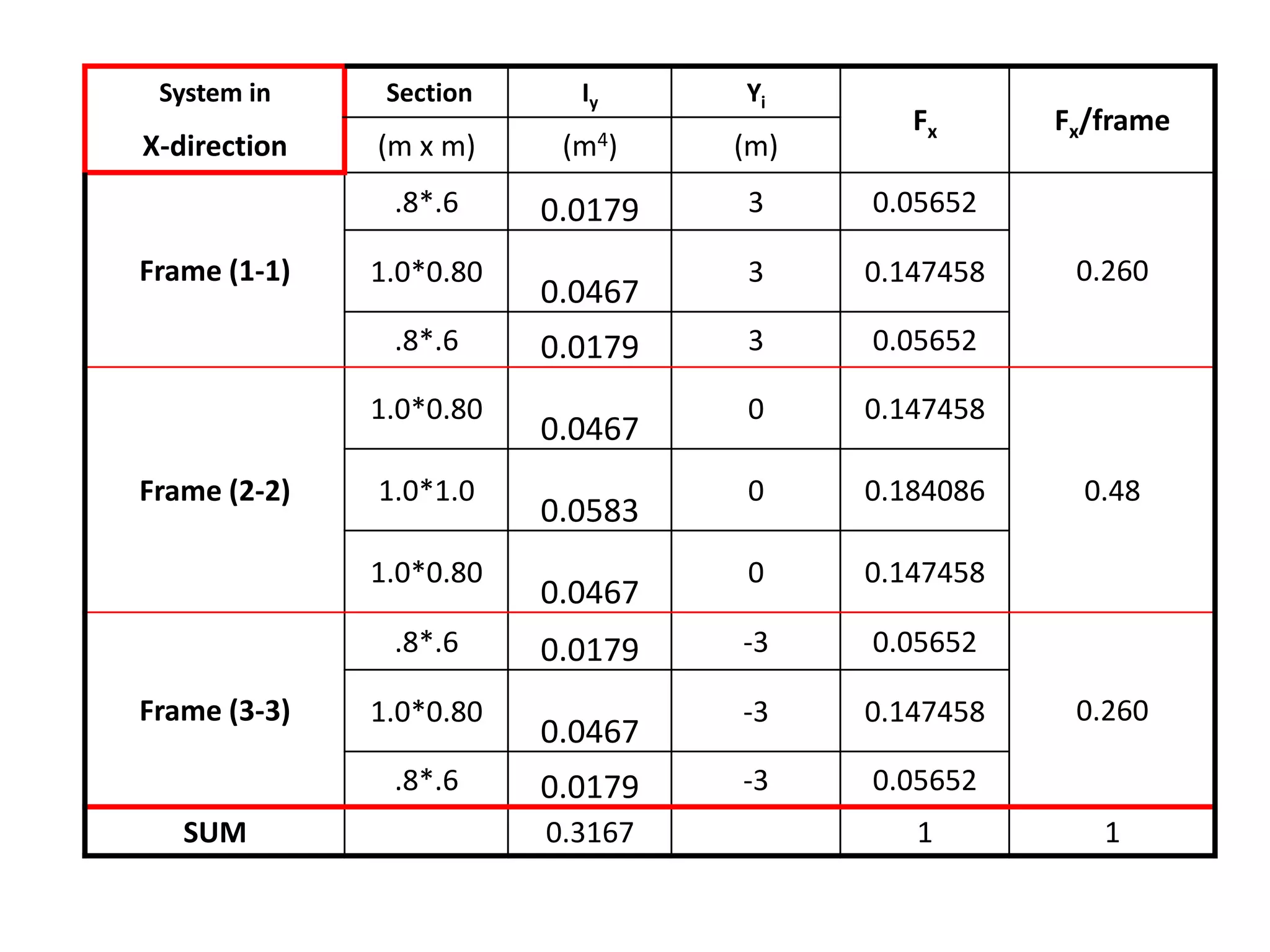
40. System
in
Section Iy Yi
Iy . Yi
2 Iy . Yi Fx' Fx"
Fx/
column
Fx/
frameX-
directio
n
(m x m) (m4) (m)
Frame
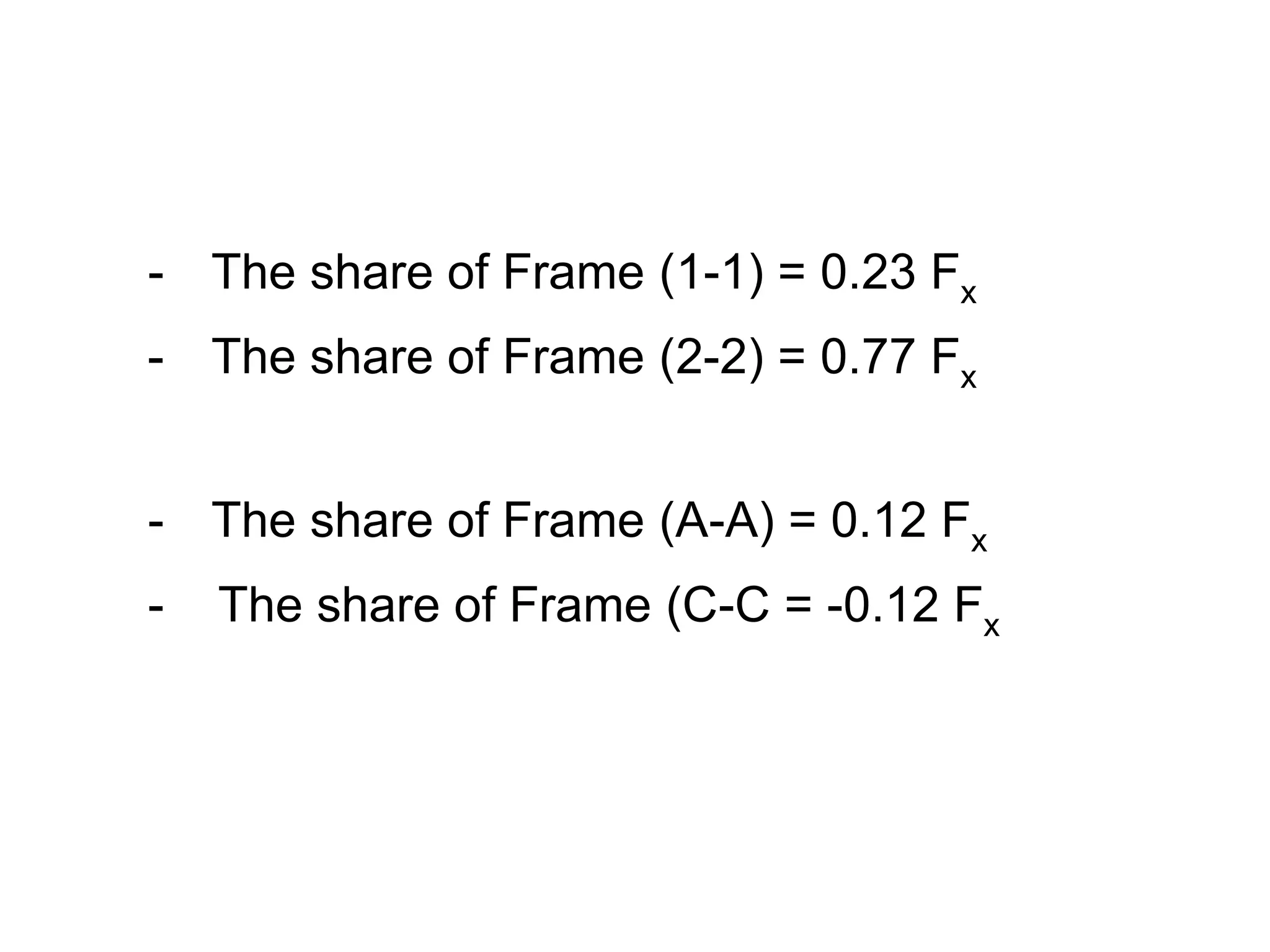
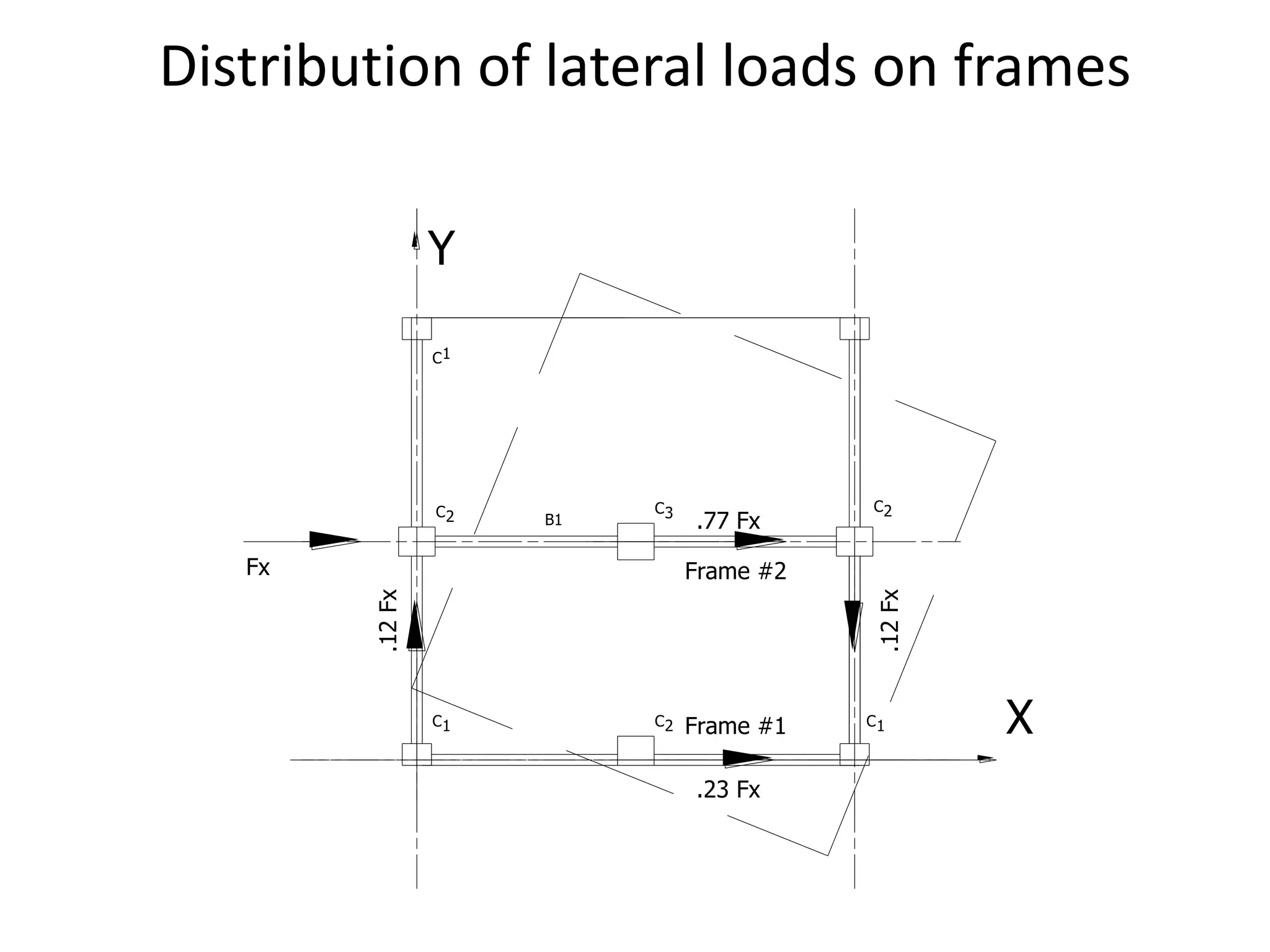
(1-1)
0.8x0.60 0.0179 -1.94 0.0674 -0.0347 0.0764 -0.027 0.050
0.231.0x0.80 0.0467 -1.94 0.1758 -0.0906 0.1994 -0.070 0.130
0.8x0.60 0.0179 -1.94 0.0674 -0.0347 0.0764 -0.027 0.050
Frame
(2-2)
1.0x0.80 0.0467 1.06 0.0525 0.0495 0.1994 0.038 0.237
0.771.0x1.00 0.0583 1.06 0.0655 0.0618 0.2489 0.047 0.296
1.0x0.80 0.0467 1.06 0.0525 0.0495 0.1994 0.038 0.237
SUM 0.2342 0.4809 1.0000 0.00 1.00 1.00
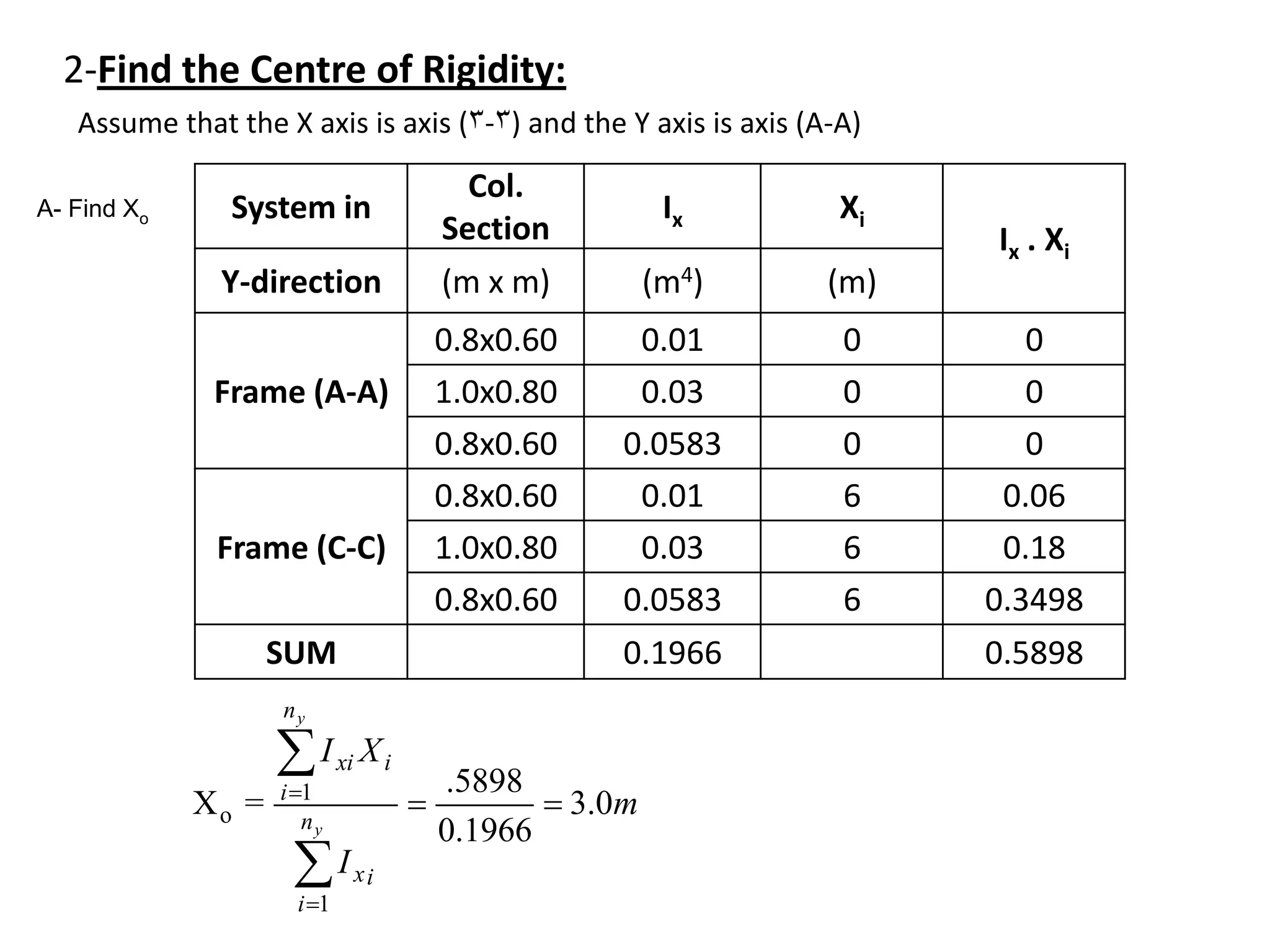
3 – find the values of [Iy. Yi
2 ] in the X - direction

41. System in Section Ix Xi
Ix. Xi
2 Ix. Xi Fy' Fy"
Fy/
column
Fy/
Frame
Y-direction (m x m) (m4) (m)
Frame
(A-A)
0.8x0.60 0.01008 -3 0.0907 -0.0302 0.0000 0.023 0.023
0.121.0x0.8 0.02987 -3 0.2688 -0.0896 0.0000 0.069 0.069
0.8x0.6 0.01008 -3 0.0907 -0.0302 0.0000 0.023 0.023
Frame
(C-C)
0.8x0.6 0.01008 3 0.0907 0.0302 0.0000 -0.023 -0.023
-0.121.0x0.8 0.02987 3 0.2688 0.0896 0.0000 -0.069 -0.069
0.8x0.6 0.01008 3 0.0907 0.0302 0.0000 -0.023 -0.023
SUM 0.1001 0.9005 0.0000 0.0000 0.0000 0.0000 0.0000
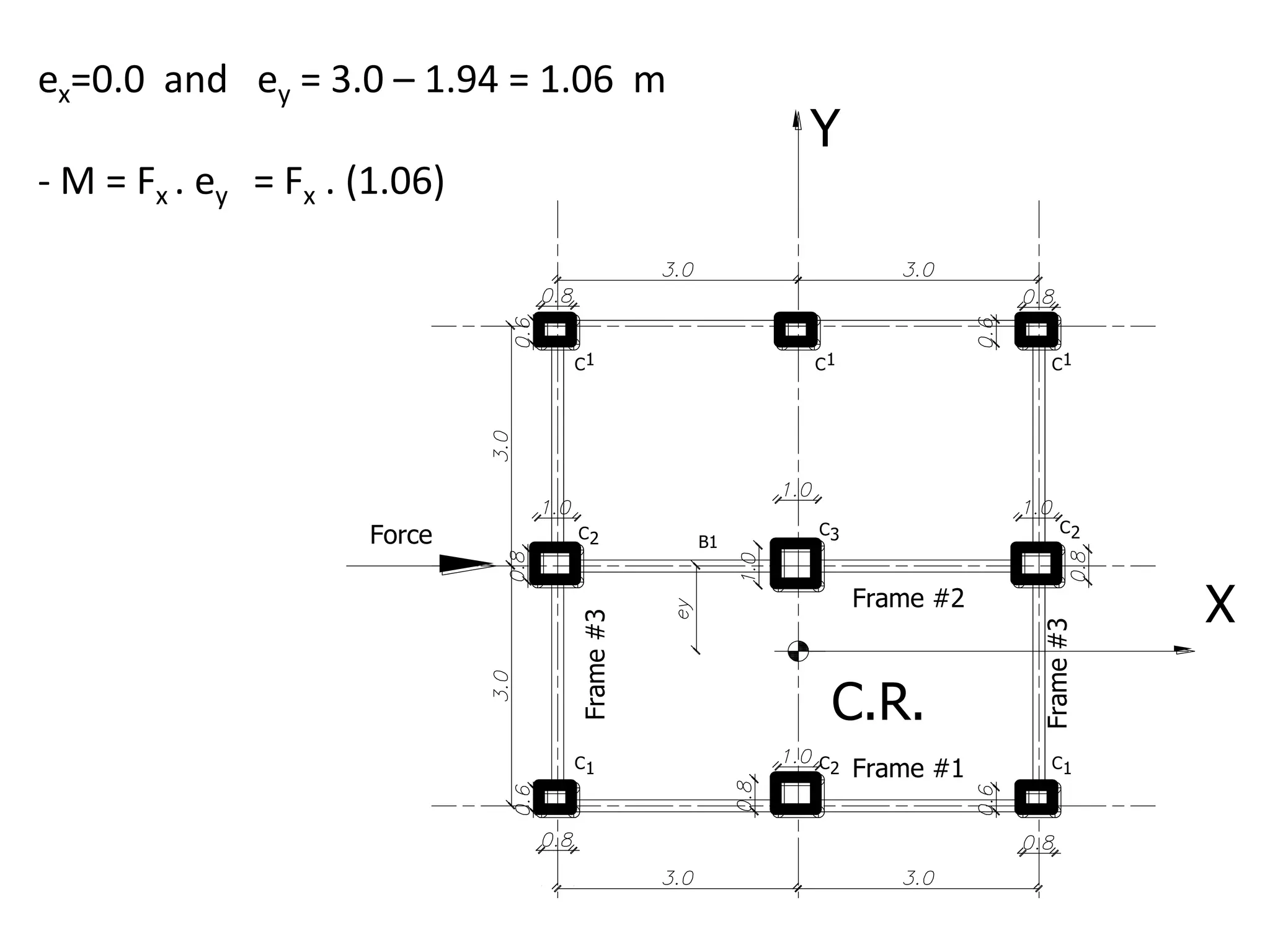
4– Calculate the values of [Ix. Xi
2 ] in the Y - direction

42. - The share of Frame (1-1) = 0.23 Fx
- The share of Frame (2-2) = 0.77 Fx
- The share of Frame (A-A) = 0.12 Fx
- The share of Frame (C-C = -0.12 Fx

43. .12Fx
.12Fx
C1
.23 Fx
.77 Fx
Fx
3C
1C1C C2
Y
X
B12C 2C
Frame #1
Frame #2
Distribution of lateral loads on frames