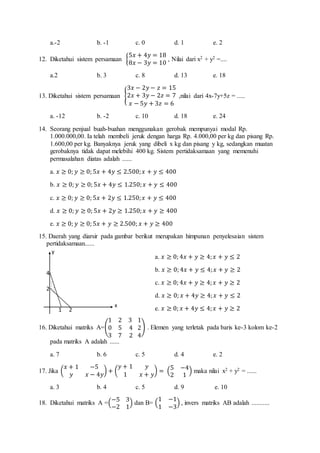
Dokumen ini adalah soal ujian matematika untuk kelas X dengan berbagai jenis pertanyaan, seperti bentuk aljabar, pertidaksamaan, sistem persamaan linear, dan konsep fungsi. Terdapat 30 pertanyaan yang mencakup topik-topik dasar dalam matematika. Tugas siswa adalah memilih jawaban yang paling tepat untuk setiap soal.

1. Mata Pelajaran : Matematika
Kelas : X MIA/ X IIS
Pilihlah salah satu jawaban yang paling tepat !
1. Bentuk
9𝑝−6
𝑞5
27𝑝−7 𝑞5 dapat dinyatakan sebagai .......
a.
1
3𝑝
b.
1
3𝑞
c.
3
𝑝
d.
𝑞
3
e.
𝑝
3
2. Bentuk
1𝑎𝑏
8𝑎−3 𝑏5 dapat dinyatakan sebagai .......
a.
1
3𝑎𝑏
b.
1
8𝑎 𝑏4 c.
𝑎 𝑠
8𝑏4 d.
𝑎
8𝑏4 e.
𝑎 𝑠
𝑏4
3. Bentuk
13
2−√3
sama dengan ......
a.13 (2+ √3) b. 13 (2 − √3) c.
13
7
(2 − √3) d. 2 − √3 e. 2 + √3
4. Bentuk
5
3+√8
sama dengan ......
a.5 (9+ √8) b. 5 (3 − √8) c.
5
2
(3 − √8) d. 3 − √8 e.3 + √8
5. Bentuk sederhana dari 2√175 − 5√343+ √63− 3√112adalah .......
a.−29√7 b. −31√7 c. −32√7 d. −34√7 e. −37√7
6. Bentuk sederhana dari 3√75 − √48 + √243 − 5√12 adalah .......
a.−11√7 b. −10√7 c. 8√7 d. 10√7 e. 37√7
7. Nilai dari 5 log27 . 9 log 625 adalah .....
a.6 b. 3 c. 1 d.
8
3
e.
2
3
8. Nilai dari 3 log16 . 4 log 243 adalah .....
a.20 b. 10 c. 5 d.
5
2
e.
2
5
9. Jika 7 log 2 = a dan 2 log 3 = b, maka 6 log 98 sama dengan ......
a.
𝑎
𝑎+𝑏
b.
𝑎+2
𝑏+1
c.
𝑎+2
𝑎( 𝑏+1)
d.
𝑎+1
𝑏+2
e.
𝑎+2
𝑏( 𝑎+1)
10. Jika 3 log 2 = a dan 3 log 5 = b, maka 10 log 250 sama dengan ......
a.
𝑎
𝑎+𝑏
b.
𝑎+2
𝑏+1
c.
𝑎+2
𝑎( 𝑏+1)
d.
𝑎+1
𝑏+2
e.
𝑎+2
𝑏( 𝑎+1)
11. Nilai x yang memenuhi persamaan
𝑥+9
3
=
3𝑥+2
4
adalah ....
a.0 b. 2 c. 4 d. 6 e. 8
12. Untuk persamaan 7𝑥 + 3( 𝑥 − 1) = 2(3𝑥 − 5) + 5( 𝑥 + 1) adalah .....
a.-5 b. -3 c. -1 d. 2 e. 4
13. Agar pertidak samaan 2𝑥 − 5 > 5𝑥 + 4 benar maka nilai x yang memenuhi adalah .....
a. 𝑥 > 3 b. 𝑥 > −3 c. 𝑥 < −3 d. 𝑥 < 3 e. 𝑥 > 6
14. Tentukan himpunan penyelesaian dari pertidaksamaan |3𝑥 − 6| < 9 adalah .....
a.{ 𝑥| 𝑥 > 5} c. { 𝑥| 𝑥 < −1} e. { 𝑥|−3 < 𝑥 < 15}
b. { 𝑥|−1 < 𝑥 < 5} d. { 𝑥| 𝑥 < −1 𝑎𝑡𝑎𝑢 𝑥 > 5}
10. Nilai-nilai x yang memenuhi pertidaksamaan |
𝑥
4
+ 6| ≥ 2 adalah ......
a. { 𝑥| 𝑥 ≤ 2 𝑎𝑡𝑎𝑢 𝑥 ≥ 8} c. { 𝑥| 𝑥 ≤ 1 𝑎𝑡𝑎𝑢 𝑥 ≥ 2} e. { 𝑥|−16 ≤ 𝑥 ≤ −32}
b. { 𝑥|8 ≤ 𝑥 ≤ 16} d. { 𝑥| 𝑥 ≤ −32 𝑎𝑡𝑎𝑢 𝑥 ≥ −16}
11. Nilai y yang memenuhi sistem persamaan linear {
5𝑥 + 2𝑦 = 13
3𝑥 − 7𝑦 = 16
,adalah .....

2. a.-2 b. -1 c. 0 d. 1 e. 2
12. Diketahui sistem persamaan {
5𝑥 + 4𝑦 = 18
8𝑥 − 3𝑦 = 10
, Nilai dari x2 + y2 =....
a.2 b. 3 c. 8 d. 13 e. 18
13. Diketahui sistem persamaan {
3𝑥 − 2𝑦 − 𝑧 = 15
2𝑥 + 3𝑦 − 2𝑧 = 7
𝑥 − 5𝑦 + 3𝑧 = 6
,nilai dari 4x-7y+5z = .....
a. -12 b. -2 c. 10 d. 18 e. 24
14. Seorang penjual buah-buahan menggunakan gerobak mempunyai modal Rp.
1.000.000,00. Ia telah membeli jeruk dengan harga Rp. 4.000,00 per kg dan pisang Rp.
1.600,00 per kg. Banyaknya jeruk yang dibeli x kg dan pisang y kg, sedangkan muatan
gerobaknya tidak dapat melebihi 400 kg. Sistem pertidaksamaan yang memenuhi
permasalahan diatas adalah ......
a. 𝑥 ≥ 0; 𝑦 ≥ 0; 5𝑥 + 4𝑦 ≤ 2.500; 𝑥 + 𝑦 ≤ 400
b. 𝑥 ≥ 0; 𝑦 ≥ 0; 5𝑥 + 4𝑦 ≤ 1.250; 𝑥 + 𝑦 ≤ 400
c. 𝑥 ≥ 0; 𝑦 ≥ 0; 5𝑥 + 2𝑦 ≤ 1.250; 𝑥 + 𝑦 ≤ 400
d. 𝑥 ≥ 0; 𝑦 ≥ 0; 5𝑥 + 2𝑦 ≥ 1.250; 𝑥 + 𝑦 ≥ 400
e. 𝑥 ≥ 0; 𝑦 ≥ 0; 5𝑥 + 𝑦 ≥ 2.500; 𝑥 + 𝑦 ≥ 400
15. Daerah yang diarsir pada gambar berikut merupakan himpunan penyelesaian sistem
pertidaksamaan......
a. 𝑥 ≥ 0; 4𝑥 + 𝑦 ≥ 4; 𝑥 + 𝑦 ≤ 2
b. 𝑥 ≥ 0; 4𝑥 + 𝑦 ≤ 4; 𝑥 + 𝑦 ≥ 2
c. 𝑥 ≥ 0; 4𝑥 + 𝑦 ≥ 4; 𝑥 + 𝑦 ≥ 2
d. 𝑥 ≥ 0; 𝑥 + 4𝑦 ≥ 4; 𝑥 + 𝑦 ≤ 2
e. 𝑥 ≥ 0; 𝑥 + 4𝑦 ≤ 4; 𝑥 + 𝑦 ≥ 2
16. Diketahui matriks A=(
1 2 3
0 5 4
3 7 2
1
2
4
) . Elemen yang terletak pada baris ke-3 kolom ke-2
pada matriks A adalah ......
a. 7 b. 6 c. 5 d. 4 e. 2
17. Jika (
𝑥 + 1 −5
𝑦 𝑥 − 4𝑦
) + (
𝑦 + 1 𝑦
1 𝑥 + 𝑦
) = (
5 −4
2 1
) maka nilai x2 + y2 = ......
a. 3 b. 4 c. 5 d. 9 e. 10
18. Diketahui matriks A =(
−5 3
−2 1
) dan B= (
1 −1
1 −3
) , invers matriks AB adalah ...........
x
y
21
4
2

3. a. (
1
2
−2
−
1
2
1
) c. (
−
1
2
−2
1
2
1
) e. (
2
1
2
−1 −
1
2
)
b. (
2 −
1
2
−1
1
2
) d. (
1
1
2
2 −
1
2
)
19. Jika matriks B = (bij) ditentukan oleh B = (
8 −2 3
2 5 −3
−1 3 2
1
4
−5
) , maka nilai dari
b13 + b21 – b34 adalah......
a. -5 b. -3 c. 0 d. 5 e. 10
20. Nilai x pada persaman |
3𝑥 4
5 2𝑥
| = 4 adalah......
a.-3 b. -2 c. -1 d. 0 e. 1
21. Didefinisikan relasi R: A→B dalam bentuk diagram panah sebagai berikut.
Daerah hasil dari relasi tersebut adalah .......
a. {1,2,3,4}
b. { 𝑎, 𝑏, 𝑐, 𝑑}
c. { 𝑎, 𝑏, 𝑐, 𝑑, 𝑒}
d. {1,2,3,4, 𝑎, 𝑏, 𝑑, 𝑒}
e. {1,2,3,4, 𝑎, 𝑏, 𝑐, 𝑑, 𝑒}
22. Diberikan himpunan P = {2, 3, 5}. Didefinisikan Relasi R pada himpunan P. Relasi R
yang memiliki sifat refleksif adalah ......
a. {(2,3), (2,5)¸(3,3)¸(3,5),(5,5)} d. {(2,5),(3,2)¸(3,3)¸(3,5),(5,5)}
b. {(2,2), (2,5)¸(3,2)¸(3,5),(5,5)} e. {(2,2),(2,3)¸(2,5)¸(3,2),(3,5)}
c. {(2,2), (2,3)¸(3,3)¸(3,5),(5,5)}
23. Diketahui fungsi f(x) = x2 +3x – 7. Tentukan nilai dari f(3) = ......
a. 8 b. 9 c. 10 d. 11 e. 12
24. Fungsi-fungsi berikut adalah fungsi-sungsi dari himpunan A = { 𝑎, 𝑏, 𝑐, 𝑑} ke himpunan B
= {1, 2, 3, 4}. Yang merupakan fungsi bijektif adalah.....
a. f = {( 𝑎,2), ( 𝑏,3)¸( 𝑐, 1)¸( 𝑑, 4)} d. f = {( 𝑎, 4),( 𝑏, 2)¸( 𝑐, 2)¸( 𝑑, 4)}
b. f = {( 𝑎, 1),( 𝑏, 4)¸( 𝑐, 2)¸( 𝑑,1)} e. f = {( 𝑎, 1),( 𝑏, 2)¸( 𝑐, 3)¸( 𝑑, 2)}
c. f = {( 𝑎, 3),( 𝑏, 1)¸( 𝑐, 4)¸( 𝑑,3)}
25. Diberikan fungsi f(x) = mx + n . Jika f(-3) = -2, dan f(5) = 22 maka nilai f(-2) + f(3) =
......
a. -9 b. -3 c. 7 d. 11 e. 17
1
2
3
4
a
b
c
d
e
A BR

4. 26. Suatu barisan bilangan mempunyai rumus suku ke –n adalah Un = 6n2 -4. Nilai U2 + U5
adalah .....
a. 166 b. 170 c. 175 d. 188 e. 190
27. Diketahui suatu barisan aritmatika -8, -5, -2, 1, ... beda dari barisan tersebut adalah .....
a. -3 b. -2 c. 1 d. 2 e. 3
28. Suatu barisan aritmatika 93, 86, 79, 72, ..., 9 . Banyaknya suku barisan itu adalah ......
a. -9 b. -3 c. 7 d. 11 e. 13
29. Diketahui suatu barisan aritmatika 303, 300, 297, 294, .... Suku ke-101 dari barisan
tersebut adalah....
a. 603 b. 103 c. 53 d. 13 e. 3
30. Jumlah 10 suku pertama dari barisan aritmatika 100, 94, 88, 82, ..., adalah ......
a. 2014 b. 1070 c. 214 d. 107 e. 254