This document discusses temporal logics for verification including Linear Temporal Logic (LTL) and Metric Temporal Logic (MTL) and their applications to different models like words, timed words, and data words. It introduces the syntax and semantics of LTL, MTL, and extensions of MTL to these different models. It also discusses different decision problems like satisfiability, model checking, and path checking for these logics and complexity results for different classes of structures. Finally, it advertises an open call for a research training group on quantitative logics and automata.

1. Metric Temporal Logic over Data Words
Seminar Oxford Women in Computer Science
Karin Quaas
University of Leipzig
3.3.2015

2. Verification
- Program P, Specification S
- Does the program P satisfy the specification S?
- Verification: Can one automatically verify whether P satisfies S?
- P...abstract model: finite automata, timed automata, one-counter automata etc.
- S...logical formula: FOL, LTL, MTL, etc.
Other Usage
- You may also use the logics I introduce for representing knowledge in a database

3. Linear Time Temporal Logic (LTL)
P... a finite set of propositional variables.
ϕ ::= true | p | ¬ϕ | ϕ ∨ ϕ | ϕUϕ | Xϕ
where p ∈ P.
Syntactical abbreviations:
ϕ1 → ϕ2 ··= ¬ϕ1 ∨ ϕ2, ϕ1 ∧ ϕ2 ··= ¬(¬ϕ1 ∨ ¬ϕ2), Fϕ ··= trueUϕ, Gϕ ··= ¬F¬ϕ
U ... Until; X ... Next; F ... Finally; G ... Globally
Examples:
P = {red, green, button pressed, . . . }
ψ1 = redUbutton pressed ψ2 = button pressed → Xgreen
ψ3 = button pressed → Fgreen ψ4 = G(green ∨ red)
w =

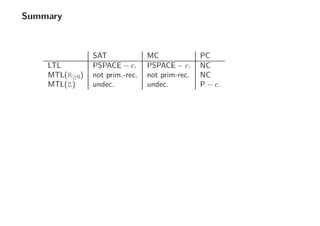
4. Verification Problems for LTL
The Satisfiability Problem
Given: An LTL formula
Question: Does there exist a word that satisfies the formula?
The Model Checking Problem
Given: An LTL formula, and an abstract model that generates/recognizes words
Question: Does every word generated/recognized by the model satisfy the formula?
The Path Checking Problem
Given: An LTL formula, a word
Question: Does the word satisfy the formula?
- Satisfiability and model checking of Kripke structures is PSPACE-complete
[Sistla & Clarke, 1985]
- Path checking for LTL is in NC [Kuhtz & Finkbeiner, 2009]

5. LTL cannot express quantitative information
Examples:
• ψ3 = button pressed → Fgreen
w =
Finally...but when?
• ψ2 = button pressed → Xgreen
w =
When the next event occurs...but when?
Goal:
We want to express that green holds within 40 seconds after button pressed.

6. Verification Problems for MTL over Timed Words
The Satisfiability Problem
Given: An MTL formula
Question: Does there exist a timed word that satisfies the formula?
The Model Checking Problem
Given: An MTL formula, and a timed automaton (recognizing timed words)
Question: Does every timed word recognized by the timed automaton
satisfy the formula?
The Path Checking Problem
Given: An MTL formula, a timed word
Question: Does the timed word satisfy the formula?
- Satisfiability is EXPSPACE-complete for timed words over N
[Alur & Henzinger, 1993]
- Satisfiability and model checking is decidable [Ouaknine & Worrell, 2005]
- Path checking for MTL is in NC [Bundala & Ouaknine, 2014]

7. Timed Words vs Data Words
Timed words are a special case of data words: monotonically increasing
w =
0.3 92.11.8 10.3 12.0 32.0 40.5 68.1 70.2
(Timed word)
Many sequences of data are not monotonically increasing.

9. MTL over Data Words
Example:
• ψ6 = F red ∧ X>0true ∧ F=0green
w =
15 2313 18 30 37 30 27 27
Goal:
We want to express, e.g., that the invention of LTL led to an increase in
the number of “coding women”, and that the number of “coding women” in
the year when LTL was invented is equal to the number when MTL was invented.

10. MTL over Data Words
Example:
• ψ6 = F red ∧ X>0true ∧ F=0green
w =
15 2313 18 30 37 30 27 27
Syntax:
P... a finite set of propositional variables.
ϕ ::= true | p | ¬ϕ | ϕ ∨ ϕ | ϕUIϕ | XIϕ
where p ∈ P, I ⊆ Z is an interval.
Syntactical abbreviations: FIϕ ··= trueUIϕ, GIϕ ··= ¬FI¬ϕ

11. Verification Problems for MTL over Data Words
The Satisfiability Problem
Given: An MTL formula
Question: Does there exist a data word that satisfies the formula?
The Model Checking Problem
Given: An MTL formula, and a one-counter machine (simulating data words)
Question: Does every run of the one-counter machine satisfy the formula?
The Path Checking Problem
Given: An MTL formula, a data word
Question: Does the data word satisfy the formula?
- Model checking is undecidable, decidable for deterministic one-counter
machines [Q, 2013]
- Satisfiability is undecidable [Carapelle, Feng, Gil, & Q 2014]
- Path checking for MTL is in P-complete [Feng, Lohrey, & Q, 2015 (not pub.)]

12. Summary
SAT MC PC
LTL PSPACE − c. PSPACE − c. NC
MTL(R≥0) not prim.-rec. not prim-rec. NC
MTL(Z) undec. undec. P − c.

13. Quantitative Logics and Automata
- DFG Research Training Group QuantLA in Leipzig/Dresden
- Quantitative Logics and Automata, and their applications in verification,
knowledge representation, natural language processing, and semi-structured
data (XML)
- Offers 8 doctoral scholarships starting from October 1, 2015
- Application deadline: May 15, 2015