The document discusses temporal logic and model checking, emphasizing their importance in formal methods for critical systems such as medical devices and industrial control. It covers various aspects of model checking, including syntax, semantics, and the application of temporal logic in verifying concurrent systems. Examples of safety and liveness properties are provided, alongside challenges like state explosion and the need for effective tools in automatic verification.

1. Temporal Logic & Model
Checking
Dr. Jayaraj Poroor

2. Formal methods: Why?
REAL DEVELOPMENT
IDEAL DEVELOPMENT
Specification
¯
Design
¯
Coding
¯
Testing
¯
Product
….
+ DErrors
¯
+ DErrors
¯¯
+ DBugs
¯¯¯
Limited Coverage
¯
with safety issues

3. Formal methods: Where?
Life Critical Mission Critical
Medical Devices
Therac-25
Space Vehicles
Ariane-5
Industrial Control
Slammer Worm
at Davis-Besse Plant
• An Investigation of Therac-25 Accidents [Leveson, Turner, 93]
• Ariane 5 Flight 501 Failure, Report by Inquiry Board [Lions, 96]
• Slammer worm crashed Ohio nuke plant network, News Report
[http://www.securityfocus.com/news/6767, 03]

4. Sentences (Syntax) and Models
(Semantics)
“Every PhD student must have an advisor who is a
member of faculty”
F = "x× phd-student(x) Þ $y × advisor-of(y, x) Ù faculty(y)
What does F mean?
◦ Classical Interpretation - A mathematical structure with:
◦ advisor-of mapped to a binary relation on the structure
◦ phd-student, faculty mapped to unary relations
◦ Logical symbols (Ù, Þ) have fixed interpretation
◦ Quantifiers (",$) range over elements of the underlying set
Model of F = a satisfying interpretation for F

5. Fundamental reasoning tasks
M satisfies F ? Model checking problem
? satisfies F Satisfiability problem
* satisfies F Validity problem
{ a : M |= F(a)} Formula (query) evaluation
Note: |= denotes satisfies relation

6. Modal Logic
Modalities: Necessity, knowledge, belief,
obligation, tense
◦ Symbolic Logic [Lewis,32]
Possible World Semantics
◦ Kripke Structure
Temporal Logic
◦ Time and Modality [Prior,57]
◦ Temporal modalities: always (), eventually ()

7. Possible Worlds & Kripke Structure
for a washing machine
idle
spinning
outlet-open
Kripke Structure = (States, ®,
washing
Accessibility Relation: { }
inlet-open
outlet-open
 alarm
Ø(spinning Ù washing)
 Ø(inlet-open Ù outlet-open)
L)
L : States ® 2AP
alarm

8. Verification: Sequential Programs
◦ Assigning Meanings to Programs [Floyd,67]
◦ An Axiomatic basis for Computer
Programming [Hoare, CACM69] (Hoare Logic)
◦ Guarded commands, non-determinism and
formal derivation of programs [Dijstra,75]
(GCL)

9. Hoare Logic
(Assignment Axiom)
(Conditional Rule)
(Sequencing Rule)
;
Proof Tableaux
(Pre-strengthening, Post-weakening)

10. Hoare Logic Example
P = if (x > y) then z := x else z := y
Prove that: {true} P {z = max(x,y)}
{true} if (x > y) then
{x > y}
{x = max(x,y)} {z = max(x,y)}
z := x
else
z := y
{true}
{Ø(x > y)}
{z = max(x,y)}
{z = max(x,y)}
{y = max(x,y)}
x > y Þ x = max(x,y)
x £ y Þ y = max(x,y)

11. Concurrency
Simple pre-condition/post-condition
assertions insufficient
◦ Deadlocks, Data races, Starvation!
◦ Need a language for expressing concurrency
properties
Cannot ignore intermediate steps!
◦ P ; Q : Intermediate states of P & Q do not
interleave/interact
◦ P || Q : Intermediate states interleave/interact
(in exponential number of ways)

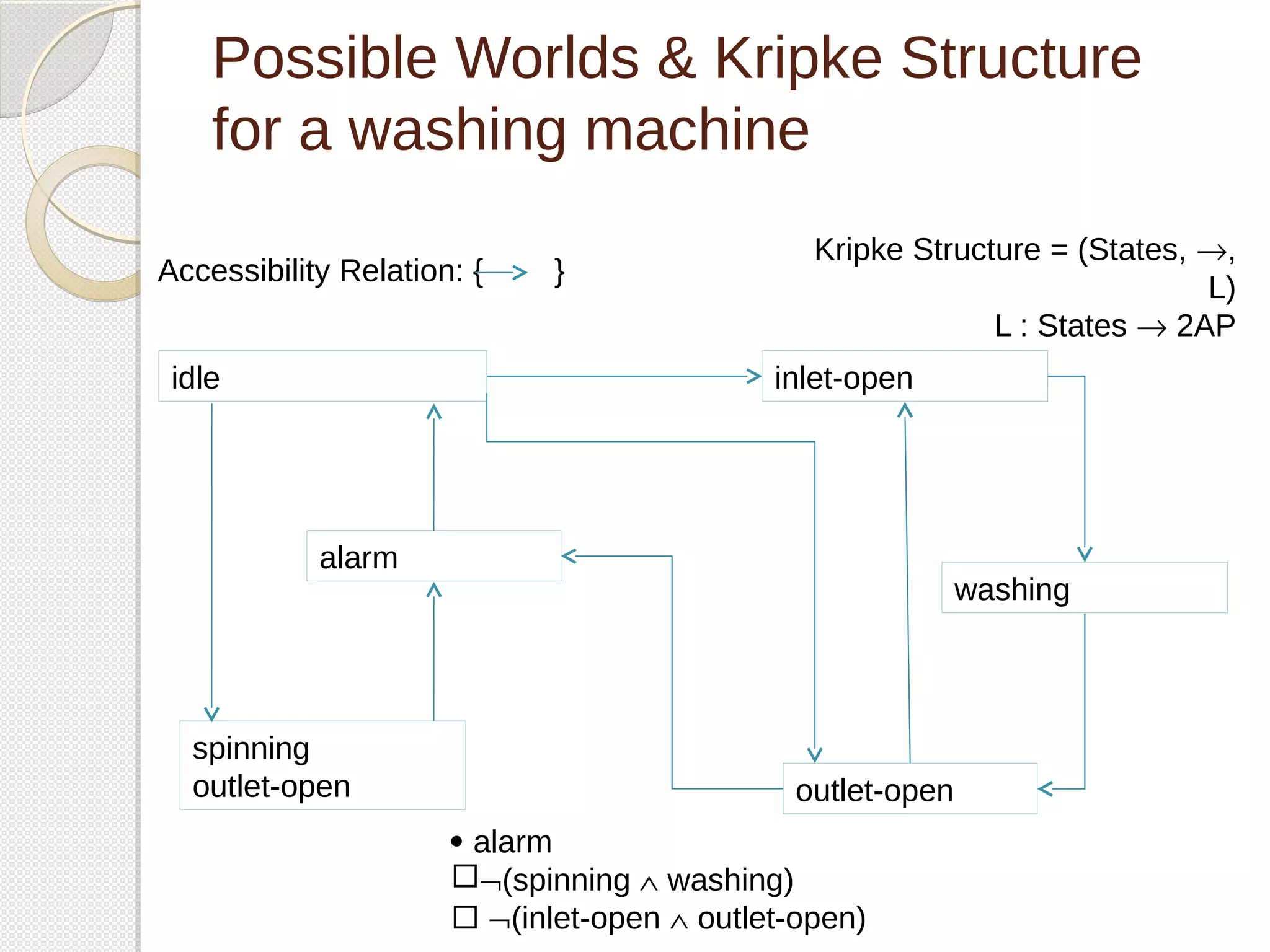
12. Specifying properties of concurrent
systems
Language: Temporal Logic
The Temporal Logic of Programs [Pnueli,77] (Linear Temporal Logic)
Safety
◦ something bad will never happen:
◦  Ø(spinning Ù washing)
Liveness
◦ Something good will eventually happen:
◦  alarm
Fairness
◦ Always something good will eventually happen
◦   idle

13. Why Temporal Logics?
Computational
System
Modal and
Temporal
Logics
Operational
Semantics models of
Labelled Transition System
(Kripke Structure)
[Stirling03] http://www.fing.edu.uy/inco/eventos/wssa/

14. Producer-Consumer with 1-buffer
Producer
wtp: while (!isempty);
csp: buf = produce();
flp : isempty = false;
Consumer
wtc: while (isempty);
csc: consume(buf);
flc : isempty = true;

15. State space for 1-buffer
system
States = control state ´ data state
= {wtp,csp,flp} ´ {wtc,csc,flc} ´ {da} ´ {em}
wt : wait
cs : critical section
fl : flag update
da : buf has data available
em : isempty is true
e.g., (wtp, csc, ,em) Î States

16. LTS for 1-buffer system
wtp, wtc, ,em
csp, wtc,da,em
flp, wtc,da,
wtp, wtc,da, flp, csc, ,
flp, flc, ,em
wtp, csc, ,
wtp, flc, ,em flp, wtc, ,em
csp, flc,da,em
flp, flc,da,
wtp, flc,da,

17. Temporal Properties for 1-buffer system
Safety:  Ø(csp Ù csc)
◦ Producer and Consumer will never be in the CS
at the same time
Liveness:  (da Ù Ø em)
◦ Eventually data will become available and empty
flag reset
Fairness:  csp
◦ Producer is always given a fair chance to produce

18. Model Checking
Model checking: M |= F?
Design & Synthesis of synchronization skeletons
using branching temporal logic [Clarke &Emerson,
81]
Specification & Verification of Concurrent Systems in
Cesar [Queille & Sifakis, 82]
Automatic Verification of Finite-State Concurrent
Systems using Temporal Logic Specifications
[Clarke, Emerson, Sistla, TOPLAS86]

19. Computations of LTS
Unfold LTS ® Infinite tree of
computations
◦ Interleaved Semantics
◦ Concurrency as non-determinism
View of computations: Linear vs
Branching
◦ Linear Temporal Logic
◦ Computational Tree Logic

20. Computational Tree Logic
Path quantifier
◦ A: All paths (inevitably)
◦ E: there Exists a path (possibly)
Temporal operator
◦ X: neXt state
◦ F: some Future state (eventually)
◦ G: Globally; all future states
◦ U: Until
e.g., AF: for all paths eventually, EG: for some path
globally

21. CTL semantics
s0 s0
M,s0 |= AF p
[Clarke, Emerson, Sistla, TOPLAS86]
M
s0
M,s0 |= AG p
M,s0 |= EF p

22. CTL examples
Logic in Computer Science [Huth, Ryan, 04]

23. Computational Tree Logic
f ::= T | F | p
| Øf | fÙf | fÚf | f®f
| AX f | EX f
| AF f | EF f
| AG f | EG f
| A [f U f] | E [f U f]
A: inevitably (along all paths)
E : possibly (there exists a path)
G: globally (always), F: in future (eventually)
X: neXt state, U: until

24. Model Checking
M |= F?
SAT(M, f) : 2S
◦ INPUT:
CTL model M = (S, ®, L)
CTL formula f
◦ OUTPUT:
Set of states (Í S)that satisfy f
◦ Complexity: O(f . |S| . (|S| + |®|))
Logic in Computer Science [Huth, Ryan,
04]

25. SAT: Conjunction &
Inevitability
y1, y2,,
y1, y2 y1 Ù y2
AFy
AFy
AFy
AFy
AFy
AFy
AFy
y y, AFy

26. SAT: Possibly Until
y1
E[y1Uy2
]
y1,
E[y1Uy2
]
E[y1Uy2
]
y2,
E[y1Uy2
]
y2

27. SAT(f) : 2S
begin
case(f)
T : return S
^ : return Æ
Øy : return S – SAT(y)
f1Ùf2 : return SAT(f1) Ç SAT(f2)
f1Úf2 : return SAT(f1) È SAT(f2)
f1Þf2 : return SAT(Øf1Úf2)
…

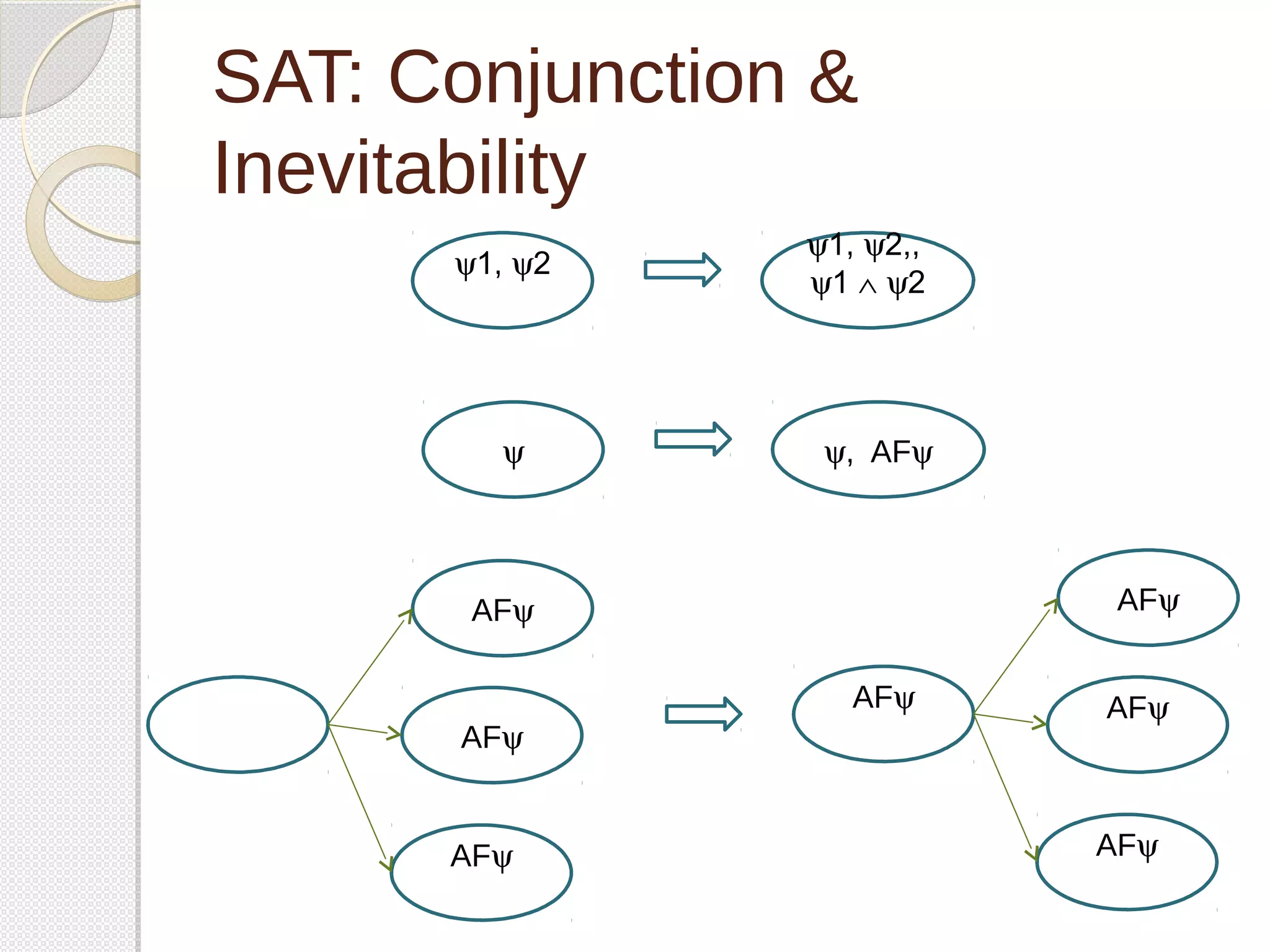
28. SAT (case(f) cont.d)
AFy : SATAF(y)
E[f1Uf2] : SATEU(f1,f2)
end case
end

29. SATAF(f)
function f(f,Y)
begin
if Y = Æ then
return SAT(f)
else
return Y È
pre"(Y)
end
begin
Y := Æ;
repeat
X := Y;
Y := f(f,Y);
until X = Y
end

30. Fixpoint characterization
Consider, F: 2S ® 2S
Formula are identified with their characteristic set
◦ e.g. f denotes set of all states where f is true
Subsets of S (Î2S) form complete lattice
◦ Partial order: Í, Join: È, Meet: Ç
Knaster-Tarski theorem
◦ “Monotone functions on a complete lattice possess least
and greatest fixpoints”: A lattice-theoretical fixpoint
theorem and its applications [Tarski,55]

31. Fixpoint characterization: Eventually,
Until
EFf = mZ. f Ú EX Z
AFf = mZ. f Ú AX Z
E[y1Uy2] = mZ. y2 Ú (y1 Ù EX Z)
A[y1Uy2] = mZ. y2 Ú (y1 Ù AX Z)

32. Fixpoint characterization: globally
AGf = nZ.fÙAX Z
EGf = nZ.fÙEX Z

33. LTL Model checking
The complexity of propositional linear
temporal logics [Sistla, Clarke, 85]
Checking that finite state concurrent programs
satisfy their linear specification, [Lichtenstein,
Pnueli, POPL85]
An automata-theoretic approach to automatic
program verification [Vardi, Wolper, 86]
◦ LTL to Buchi Automata

34. State explosion
The state explosion problem [Clarke, Grumberg, 87]
◦ Number of concurrent processes
◦ Number of variables
Partial-order reduction
◦ An Introduction to Trace Theory [Mazurkiewicz,95]
Symbolic Model Checking: 1020 states and beyond
[Burch, Clarke, McMillan, Dill, Hwang, 92]
◦ OBDD: Ordered Binary Decision Diagrams [Bryant,86]
◦ m-Calculus: Finiteness is m-ineffable [Park,74]
Abstraction
Combining theorem-proving & model checking
On-the-fly model checking

35. Some Tools
SPIN/Promela
◦ http://spinroot.com
Java Pathfinder
◦ http://javapathfinder.sourceforge.net/
NuSMV
◦ http://nusmv.irst.itc.it/

36. Thank You
Have a great day!