This document provides an overview of the Kalman filter, including its derivation and applications. It begins with an example of using a Kalman filter to estimate the position and velocity of a truck moving on rails. It then presents the general setup of the Kalman filter for estimating a stochastic dynamic system based on noisy observations. The derivation shows how to recursively calculate the optimal estimate and its error covariance. Several numerical examples are provided to illustrate Kalman filtering, including estimating a constant voltage, tracking a vehicle's position in 1D and 2D.

1. 1
ACM 116: The Kalman filter
• Example
• General Setup
• Derivation
• Numerical examples
– Estimating the voltage
– 1D tracking
– 2D tracking

2. 2
Example: Navigation Problem
• Truck on “frictionless” straight rails
• Initial position X0 = 0
• Movement is buffeted by random accelerations
• We measure the position every ∆t seconds
• State variables (Xk, Vk) position and velocity at time k∆t
Xk = Xk−1 + Vk−1∆t + ak−1∆t2
/2
Vk = Vk−1 + ak−1∆t
where ak−1 is a random acceleration
• Observations
Yk = Xk + Zk
where Zk is a noise term.
The goal is to estimate the position and velocity at all times.

3. 3
General Setup
Estimation of a stochastic dynamic system
• Dynamics
Xk = Fk−1Xk−1 + Bk−1uk−1 + Wk−1
– Xk: state of the system at time k
– uk−1: control-input
– Wk−1: noise
• Observations
Yk = HkXk + Zk
– Yk is observed
– Zk is noise
• The noise realizations are all independent
• Goal: predict state Xk from past data Y0, Y1, . . . , Yk−1.

4. 4
Derivation
Derivation in the simpler model where the dynamics is of the form
Xk = ak−1Xk−1 + Wk−1
and the observations
Yk = Xk + Zk
The objective is to find, for each time k, the minimum MSE filter based on
Y0, Y1, . . . , Yk−1
ˆXk =
k
j=1
h
(k−1)
j Yk−j
To find the filter, we apply the orthogonality principle
E((Xk −
k
j=1
h
(k−1)
j Yk−j)Y ) = 0, = 0, 1, . . . , k − 1.

5. 5
Recursion
The beautiful thing about the Kalman filter is that one can almost deduce the
optimal filter to predict Xk+1 from that predicting Xk.
h
(k)
j+1 = (ak − h
(k)
1 )h
(k−1)
j , j = 1, . . . , k.
Given the filter h(k−1)
, we only need to find h
(k)
1 to get the filter at the next
time step.

6. 6
How to find h
(k)
1 ?
Observe that the next prediction is equal to
ˆXk+1 = h
(k)
1 Yk +
k
j=1
(ak − h
(k)
1 )h
(k−1)
j Yk−j
= ak
ˆXk + h
(k)
1 (Yk − ˆXk)
Interpretation
ˆXk+1 = ak
ˆXk + h
(k)
1 Ik
• ak
ˆXk is the prediction based on the estimate at time k
• h
(k)
1 Ik is a corrective term which is available since we now see Yk
– h
(k)
1 is called the gain
– Ik = Yk − ˆXk is called the innovation

7. 7
Error of Prediction
To find h
(k)
1 , we look at the error of prediction
k = Xk − ˆXk
We have the recursion
k+1 = (ak − h
(k)
1 ) k + Wk − h
(k)
1 Zk
• 0 = Z0
• E( k) = 0
• E( 2
k+1) = [ak − h
(k)
1 ]2
E( 2
k) + E(W 2
k ) + [h
(k)
1 ]2
E(Z2
k)

8. 8
To minimize the MSE k+1, we adjust h
(k)
1 so that
∂h
(k)
1
E( 2
k+1) = 0 = −2(ak − h
(k)
1 )E( 2
k) + 2h
(k)
1 E(Z2
k)
which is given by
h
(k)
1 =
akE( 2
k)
E( 2
k) + E(Z2
k)
Note that this gives the recurrence relation
E( 2
k+1) = ak(ak − h
(k)
1 )E( 2
k) + E(W 2
k )

9. 9
The Kalman Filter Algorithm
• Initialization ˆX0 = 0, E( 2
0) = E(Z2
0 )
• Loop: for k = 0, 1, . . .
h
(k)
1 =
akE( 2
k)
E( 2
k) + E(Z2
k)
ˆXk+1 = ak
ˆXk + h
(k)
1 (Yk − ˆXk)
E( 2
k+1) = ak(ak − h
(k)
1 )E( 2
k) + E(W 2
k )

10. 10
Benefits
• Requires no knowledge about the structure of Wk and Zk (only variances)
• Easy implementation
• Many applications
– Inertial guidance system
– Autopilot
– Satellite navigation system
– Many others

11. 11
General Formulation
Xk = Fk−1Xk−1 + Wk−1
Yk = HkXk + Zk
The covariance of Wk is Qk and that of Zk is Rk.
Two variables:
• ˆXk|k estimate of the state at time k based upon Y0, . . . , Yk−1
• Ek|k error covariance matrix, Ek|k = Cov(Xk − ˆXk|k)

12. 12
Prediction
ˆXk+1|k = Fk
ˆXk|k−1
Ek+1|k = FkEk|k−1F T
k + Qk
Update
Ik = Yk − Hk
ˆXk+1|k Innovation
Sk = HkEk+1|kHT
k + Rk Innovation covariance
Kk = Ek+1|kHT
k S−1
k Kalman Gain
ˆXk+1|k+1 = ˆXk+1|k + KkIk Updated state estimate
Ek+1|k+1 = (Id − KkHk)Ek+1|k Updated error covariance

13. 13
Estimating Constant Voltage
We wish to estimate some voltage which is almost constant except for some
small random fluctuations. Our measuring device is imperfect (e.g. because of
a poor A/D conversion). The process is governed by:
Xk = X0 + Wk, k = 1, 2, . . .
with X0 = 0.5V , and the measurements are
Zk = Xk + Vk, k = 1, 2, . . .
where Wk, Vk are uncorrelated Gaussian white noise processes, with
R := Var(Vk) = 0.01, Var(Wk) = 10−5
.

14. 14
0 5 10 15 20 25 30 35 40 45 50
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Accurate knowledge of measurement variance, Rest
=R=0.01
Iteration
Voltage
estimate
exact process
measurements

15. 15
0 5 10 15 20 25 30 35 40 45 50
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Optimistic estimate of measurement variance, Rest
=0.0001
Iteration
Voltage
estimate
exact process
measurements

16. 16
0 5 10 15 20 25 30 35 40 45 50
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Pessimistic estimate of measurement variance, Rest
=1
Iteration
Voltage
estimate
exact process
measurements

17. 17
1D Tracking
Estimation of the position of a vehicle.
Let X be a state variable (position and speed), and A is a transition matrix
A =


1 ∆t
0 1

 .
The process is governed by:
Xn+1 = AXn + Wn
where Wn is a zero-mean Gaussian white noise process. The observation is
Yn = CXn + Zn
where the matrix C only picks up the position and Zn is another zero-mean
Gaussian white noise process independent of Wn.

18. 18
0 5 10 15 20 25
!4
!2
0
2
4
6
8
Time
Position
Estimation of a moving vehicle in 1!D.
exact position
measured position
estimated position

19. 19
2D Example
General setup
X(t + 1) = F X(t) + W (t), W ∼ N(0, Q),
Y (t) = HX(t) + V (t), V ∼ N(0, R)
Moving particle at constant velocity subject to random perturbations in its
trajectory. The new position (x1, x2) is the old position plus the velocity
(dx1, dx2) plus noise w.







x1(t)
x2(t)
dx1(t)
dx2(t)







=







1 0 1 0
0 1 0 1
0 0 1 0
0 0 0 1














x1(t − 1)
x2(t − 1)
dx1(t − 1)
dx2(t − 1)







+







w1(t − 1)
w2(t − 1)
dw1(t − 1)
dw2(t − 1)








20. 20
Observations
We only observe the position of the particle.


y1(t)
y2(t)

 =


1 0 0 0
0 1 0 0









x1(t)
x2(t)
dx1(t)
dx2(t)







+


v1(t)
v2(t)


Source: http://www.cs.ubc.ca/∼murphyk/Software/Kalman/kalman.html

21. 21
Implementation
% Make a point move in the 2D plane
% State = (x y xdot ydot). We only observe (x y).
% This code was used to generate Figure 17.9 of
% "Artificial Intelligence: a Modern Approach",
% Russell and Norvig, 2nd edition, Prentice Hall, in preparation.
% X(t+1) = F X(t) + noise(Q)
% Y(t) = H X(t) + noise(R)
ss = 4; % state size
os = 2; % observation size
F = [1 0 1 0; 0 1 0 1; 0 0 1 0; 0 0 0 1];
H = [1 0 0 0; 0 1 0 0];
Q = 1*eye(ss);
R = 10*eye(os);
initx = [10 10 1 0]’;
initV = 10*eye(ss);

22. 22
seed = 8; rand(’state’, seed);
randn(’state’, seed);
T = 50;
[x,y] = sample_lds(F,H,Q,R,initx,T);

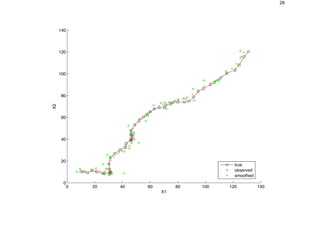
23. 23
Apply Kalman Filter
[xfilt,Vfilt] = kalman_filter(y,F,H,Q,R,initx,initV);
dfilt = x([1 2],:) - xfilt([1 2],:);
mse_filt = sqrt(sum(sum(dfilt.ˆ2)))
figure;
plot(x(1,:), x(2,:), ’ks-’);
hold on
plot(y(1,:), y(2,:), ’g*’);
plot(xfilt(1,:), xfilt(2,:), ’rx:’);
hold off
legend(’true’, ’observed’, ’filtered’, 0)
xlabel(’X1’), ylabel(’X2’)

24. 24
!40 !30 !20 !10 0 10 20
10
20
30
40
50
60
70
X1
X2
true
observed
filtered

25. 25
0 20 40 60 80 100 120 140
0
20
40
60
80
100
120
140
X1
X2
true
observed
filtered

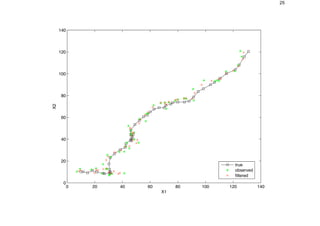
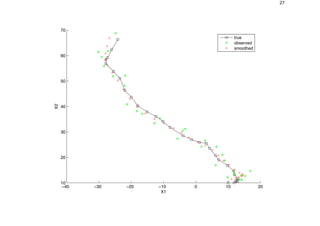
26. 26
Apply Kalman Smoother
[xsmooth, Vsmooth] = kalman_smoother(y,F,H,Q,R,initx,initV);
dsmooth = x([1 2],:) - xsmooth([1 2],:);
mse_smooth = sqrt(sum(sum(dsmooth.ˆ2)))
figure;
hold on
plot(x(1,:), x(2,:), ’ks-’);
plot(y(1,:), y(2,:), ’g*’);
plot(xsmooth(1,:), xsmooth(2,:), ’rx:’);
hold off
legend(’true’, ’observed’, ’smoothed’, 0)
xlabel(’X1’), ylabel(’X2’)

27. 27
!!0 !#0 !20 !10 0 10 20
10
20
#0
!0
50
'0
(0
)1
)2
*+,-
./0-+1-2
03..*4-2

28. 28
0 20 40 60 80 100 120 140
0
20
40
60
80
100
120
140
X1
X2
true
observed
smoothed