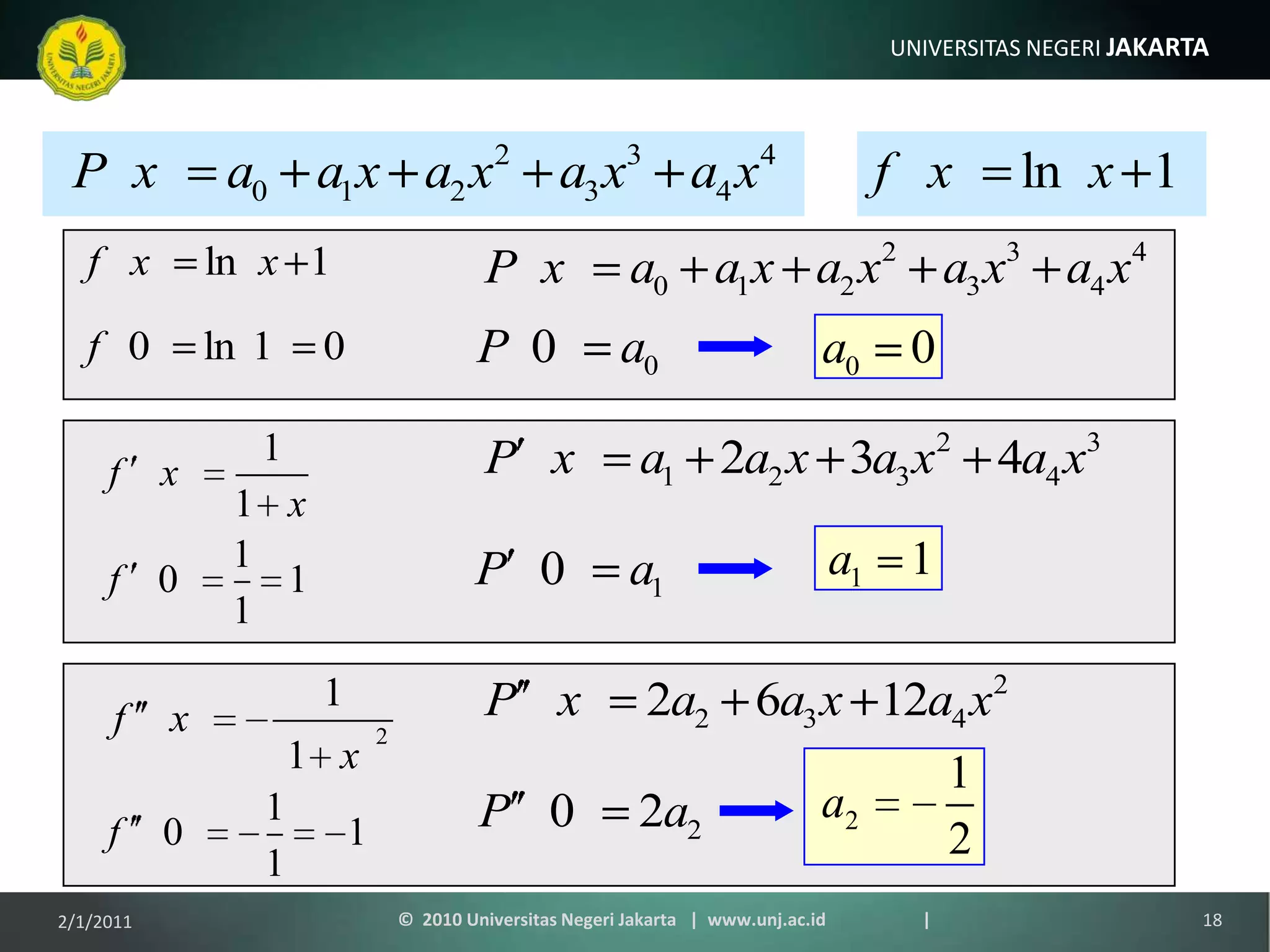
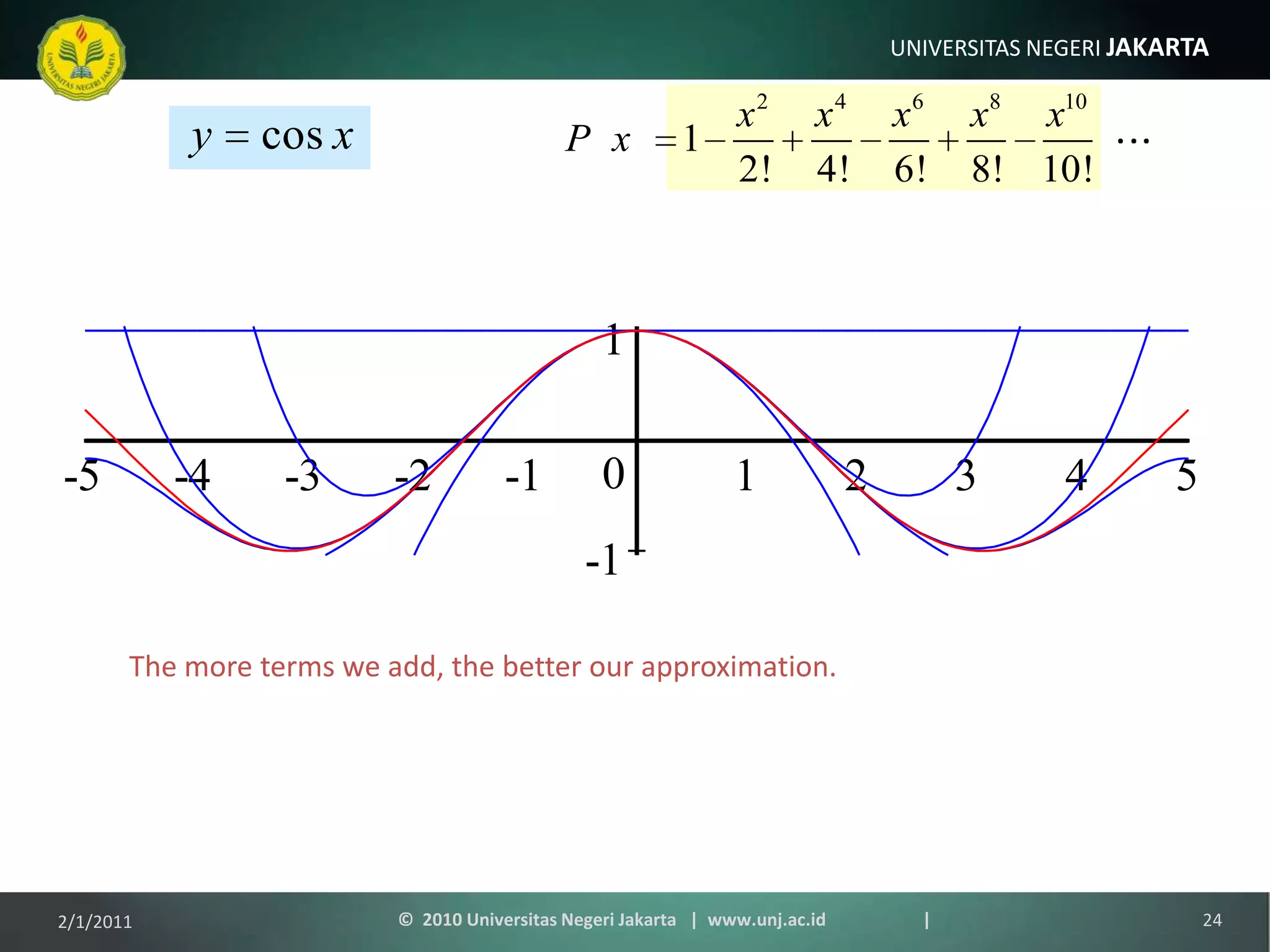
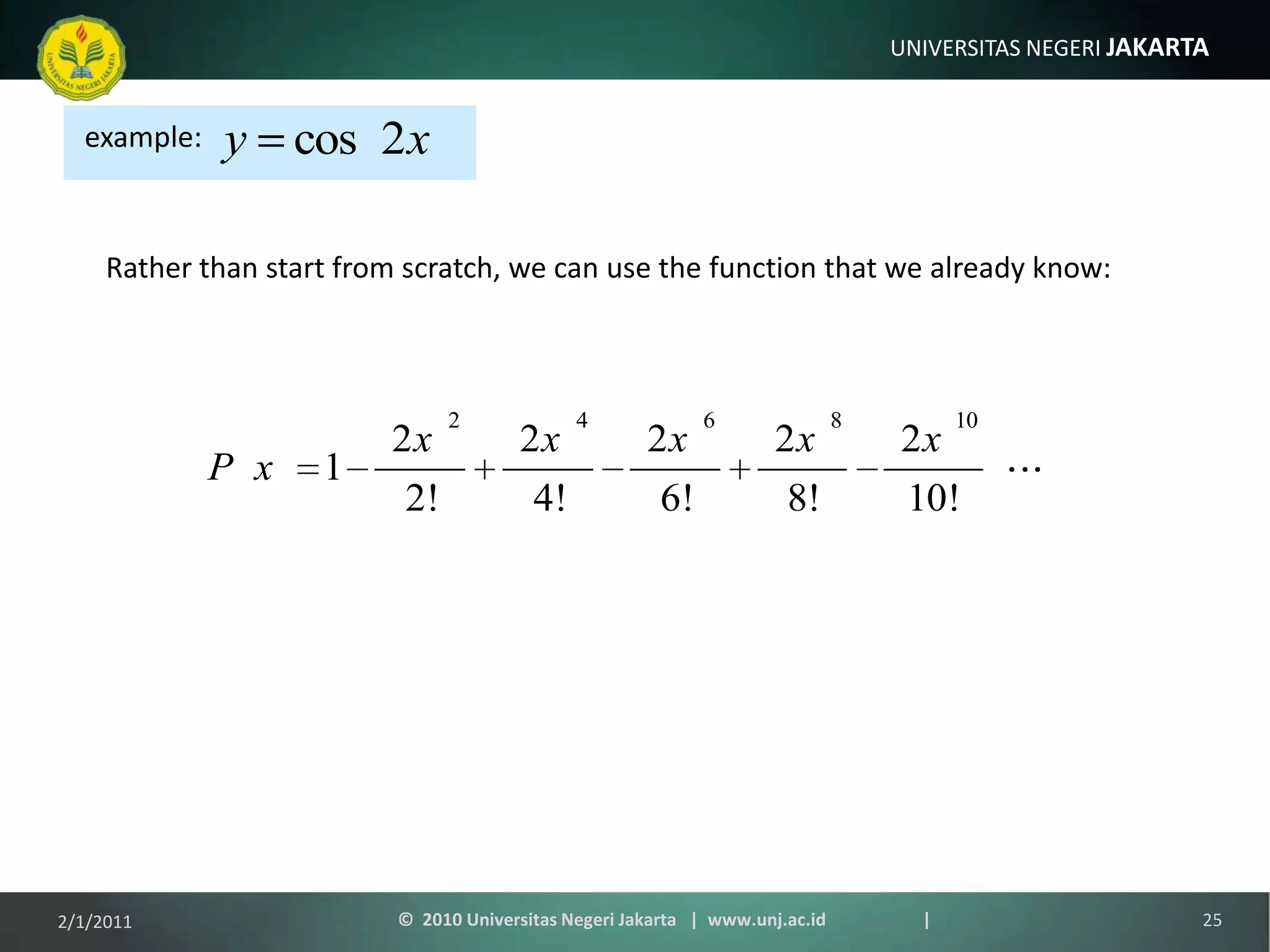
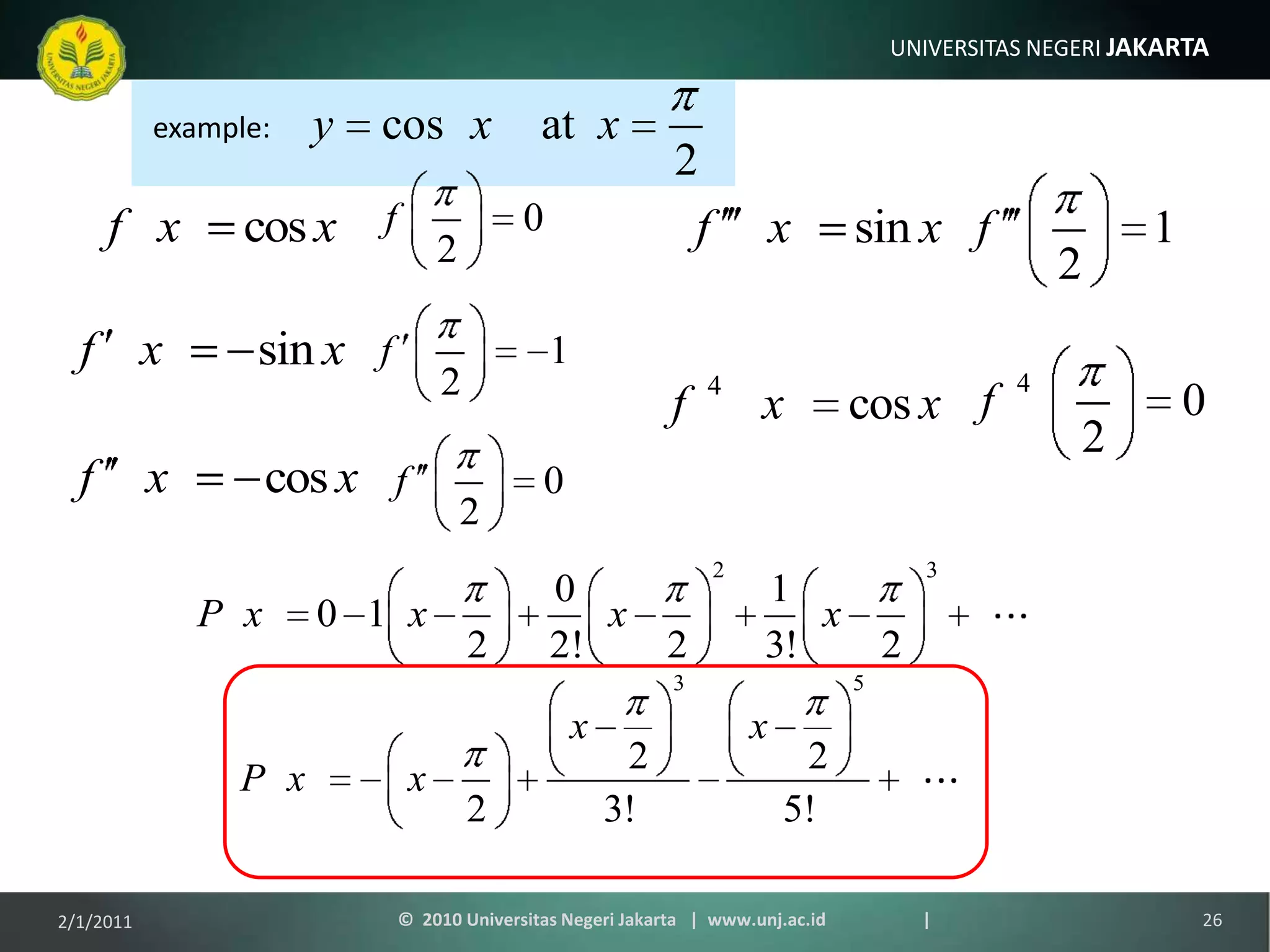
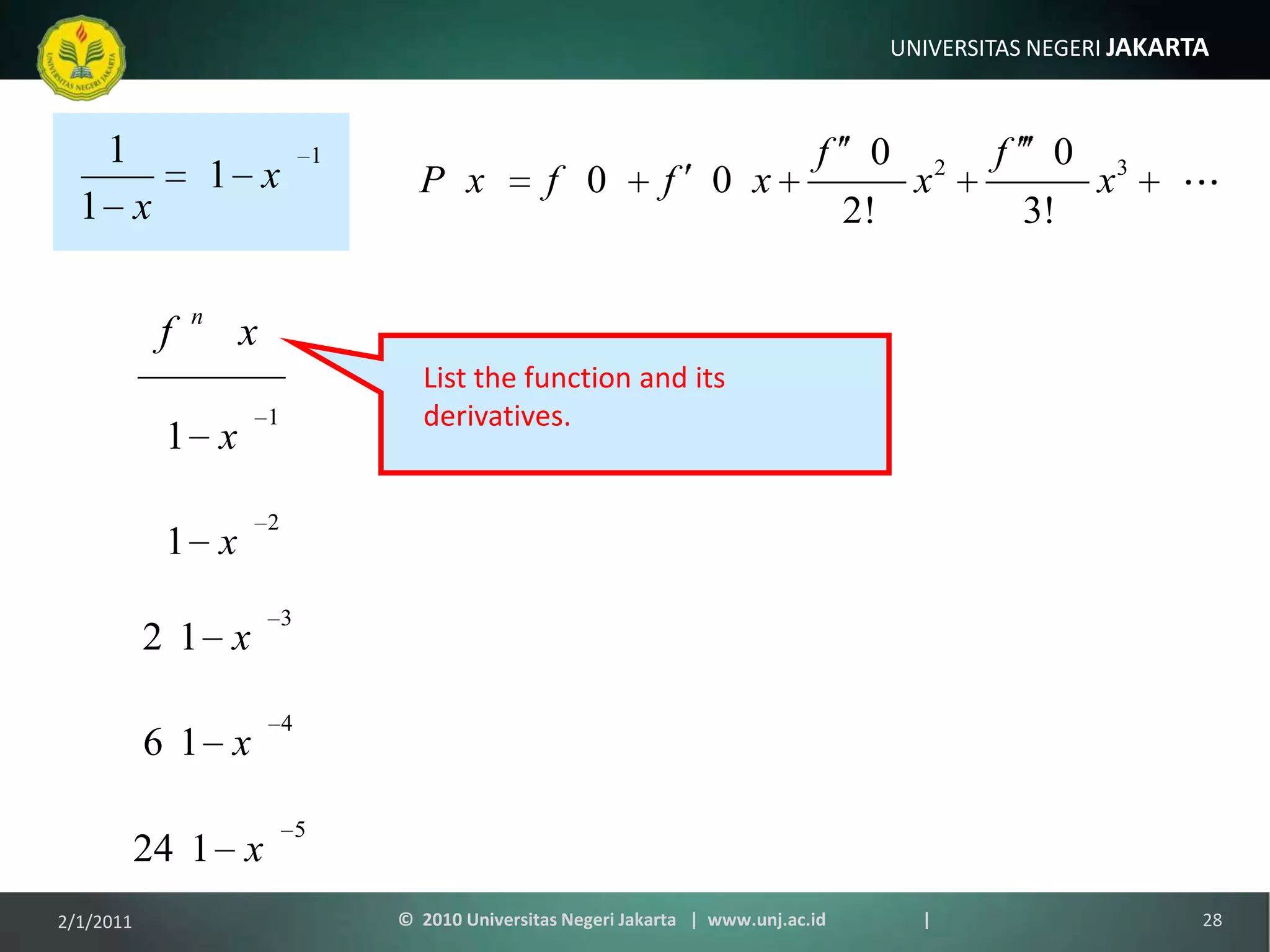
The document is a lecture on power series, Taylor series, and Maclaurin series. It introduces infinite series and provides examples of using Taylor series to approximate common functions like sine and cosine. The key points are that Taylor series can be used to approximate functions as polynomials and calculate functions to high accuracy, and Maclaurin series are a specific type of Taylor series centered at x=0. Examples are provided of deriving the Maclaurin series for exponential, sine, and cosine functions.