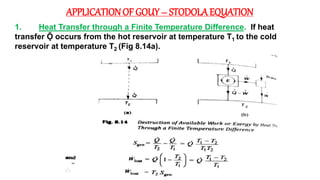
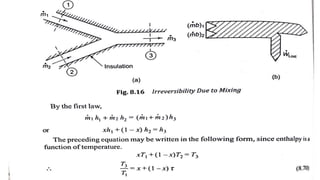
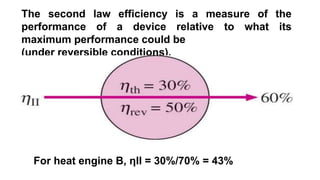
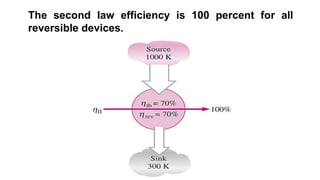
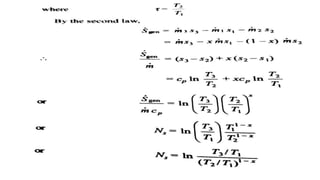The document discusses irreversibility, the Gouy-Stodola theorem, and its applications to calculating second law efficiency. It states that the Gouy-Stodola theorem establishes that the rate of exergy (available energy) loss in a process is proportional to the rate of entropy generation. It then provides examples of applying the Gouy-Stodola equation to heat transfer through a finite temperature difference, fluid flow with friction, and mixing of two fluids. Finally, it defines second law efficiency as a measure of a device's performance relative to its maximum possible reversible performance.

1. SUBMITTED BY : Nishant Narvekar
ENROLLMENT NO : 170410119061
BRANCH : SY MECH-1
IRREVERSIBILTY, GOUY-STODOLA THEOREM
AND ITS APPLICATION, SECOND LAW EFFICIENCY

2. IRREVERSIBILITY

3. Gouy-stodala Theorem:
The rate of loss of exergy (available
energy) in a process is proportional to the
rate to the rate of entropy generation.
I = Wlost = T0 (∆Suniverse) = T0Sgen

4. Gouy-stodala Theorem:
The rate of loss of exergy (available
energy) in a process is proportional to the
rate to the rate of entropy generation.
I = Wlost = T0 (∆Suniverse) = T0Sgen

5. APPLICATIONOF GOUY – STODOLA EQUATION
1. Heat Transfer through a Finite Temperature Difference. If heat
transfer Ǭ occurs from the hot reservoir at temperature T1 to the cold
reservoir at temperature T2 (Fig 8.14a).

6. If heat transfer Ǭ from T1 to T2 takes place through a reversible engine
E, the entire work output Ŵ is dissipated in the brake, from which an equal
amount of heat is rejected to the reservoir at T2 (Fig 8.14b). Heat transfer
through a finite temperature difference is equivalent to the destruction of its
availability.

7. APPLICATIONOF GOUY – STODOLA EQUATION
2. Flow of friction. Let us consider the steady and adiabatic flow of an
ideal gas through the segment of a pipe (Fig 8.15a).
By the first law,
h1 = h2
and by the second law,
Tds = dh - vdp

9. The decrease in availability or lost work is proportional to the
pressure drop (∆p) and the mass flow rate (ṁ). It is shown on the right
(Fig 8.15b) by the Grassmann diagram, the width being proportional to the
availability (or exergy) of the stream. It is an adaptation of the Sankey
diagram used for energy transfer in a plant.

10. APPLICATIONOF GOUY – STODOLA EQUATION
3. Mixing of Two Fluids. Two streams 1 and 2 of an incompressible fluid
or an ideal gas mix adiabatically at constant pressure (Fig 8.16).
Here, ṁ1 + ṁ2 = ṁ3 = ṁ(say)
Let x = ṁ1
ṁ1 + ṁ2

14. Both heat engines have the same thermal
efficiency. Are they doing equally well?
• Because B has a higher TH,
it should be able to do
better.
• Hence, it has a higher
maximum (reversible)
efficiency.
SECONDLAWEFFICIENCY

15. The second law efficiency is a measure of the
performance of a device relative to what its
maximum performance could be
(under reversible conditions).
For heat engine B, ηII = 30%/70% = 43%

16. The second law efficiency is 100 percent for all
reversible devices.

17. Second Law Efficiencies
• For heat engines = ηth/ηth,rev
• For work - producing devices = Wu/Wrev
• For work – consuming devices = Wrev/Wu
• For refrigerators and heat pumps =
COP/COPrev
• Wrev should be determined using the same
initial and final states as actual.
• And for general processes =
Exergy recovered/Exergy supplied =
1 – Exergy destroyed/Exergy supplied

18. THANKYOU