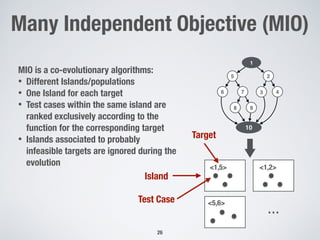
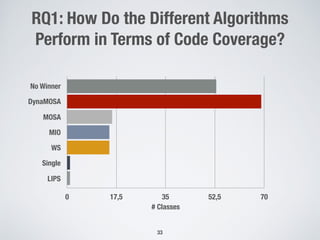
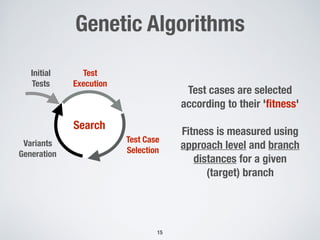
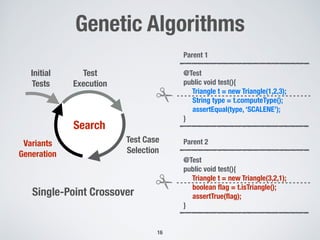
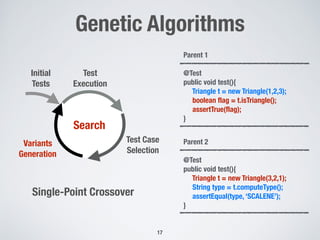
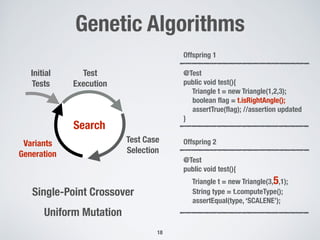
The document discusses automated test generation techniques for unit testing, focusing on search-based software testing and genetic algorithms. It highlights key concepts such as problem reformulation, test case selection, and various algorithmic approaches including many-objective sorting algorithms and whole-suite approaches. The document also presents empirical results comparing the performance of different algorithms used for code coverage in testing.

1. Automated Test Generation for
Unit Testing and Beyond
Annibale Panichella
a.panichella@tudelf.nl
@AnniPanic
1

2. Unit Testing
2
class Triangle {
int a, b, c; //sides
String type = "NOT_TRIANGLE";
Triangle (int a, int b, int c){…}
void computeTriangleType() {
1. if (a == b) {
2. if (b == c)
3. type = "EQUILATERAL";
else
4. type = "ISOSCELES";
} else {
5. if (a == c) {
6. type = "ISOSCELES";
} else {
7. if (b == c)
8. type = “ISOSCELES”;
else
9. type = “SCALENE”;
}
}
}
Class Under Test (CUT)
@Test
public void test(){
// Constructor (init)
// Method Calls
// Assertions (check)
}
Test Case
@Test
public void test(){
Triangle t = new Triangle (1,2,3);
t.computeTriangleType();
String type = t.getType();
assertTrue(type.equals(“SCALENE”));
}

3. 3
Is it that Easy?
Class = Pass2Verifier.java
Project = Apache commons BCEL

4. How to Generate Tests in
Reasonable Time?
4

5. Search-Based Software Testing
5
Computational
Intelligence
Software_
Testing_
Search
Based
Software
TestingOptimization Search
Genetic Algorithms
Ant Colony
Test Case
Coverage
Assertions
Failures

6. Search-Based Software Testing
6
Computational
Intelligence
Software_
Testing_
AI-based
Software
Testing

7. Artificial Intelligence?
7
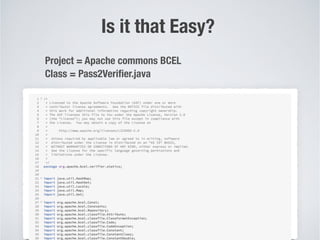
[Domingos2015 “The Master Algorithm”]
Neural Network
Regression
Support Vector
Tribe Origin Master Algorithm
Symbolists Logic, philosophy Inverse deduction
Connectionists Neuroscience Back-Propagation
Evolutionary Evolutionary biology Evolutionary Algorithms
Bayesian Statistics Probabilistic inference
Analogizers Psychology Kernel machines
Formal Methods

8. How To Apply Search?
8
Problem reformulation:
• We need to reformulate SE (or ST) problems as optimization
problems
Define an objective function:
• Define a distance function that measure how far are we to
solve the SE (or ST) problem
Choose a solver:
• Genetic Algorithm, Random Search, Hill Climbing, etc.

9. 1. Problem Reformulation
9
class Triangle {
int a, b, c; //sides
String type = "NOT_TRIANGLE";
Triangle (int a, int b, int c){…}
void computeTriangleType() {
1. if (a == b) {
2. if (b == c)
3. type = "EQUILATERAL";
else
4. type = "ISOSCELES";
} else {
5. if (a == c) {
6. type = "ISOSCELES";
} else {
7. if (b == c)
8. type = “ISOSCELES”;
else
9. type = “SCALENE”;
}
}
}
Class Under Test (CUT)
1
25
6 7 3
98
10
4
Control Flow Graph
1
5
7
9
10
Generate a test case that
covers all branches in the
selected path

10. 2. Define an Objective Function
10
1
25
6 7 3
98
10
4
Control Flow Graph
1
5
7
9
10
Generate a test case that
covers all branches in the
selected path
Well-established heuristics:
- Approach level
- Branch distance
abs(a-b) + K
If (a==b)

11. Branch Distances
11
Rules for numeric data Rules for String data
B. Korel. IEEE TSE 1990 M. ALshbraideh et al. STVR 2006

12. 3. Choose a Solver
12

13. Genetic Algorithms
13
In 1975 he wrote the
ground-breaking book on
genetic algorithms,
"Adaptation in Natural and
Artificial Systems"
John Henry Holland
P. Tonella, “Evolutionary
Testing of Classes”, ISSTA
2004

14. Genetic Algorithms
14
Test Case
Selection
Initial
Tests
Search
Test
Execution
Variants
Generation
Test Case
@Test
public void test(){
Triangle t = new Triangle(1,2,3);
String type = t.computeType();
assertEqual(type, ‘SCALENE’);
}
@Test
public void test(){
// Constructor (init)
// Method Calls
// Assertions (check)
}
Template

15. Genetic Algorithms
15
Test Case
Selection
Initial
Tests
Search
Test
Execution
Variants
Generation
Test cases are selected
according to their 'fitness'
Fitness is measured using
approach level and branch
distances for a given
(target) branch

16. 16
Test Case
Selection
Initial
Tests
Search
Test
Execution
Variants
Generation
Parent 1
@Test
public void test(){
Triangle t = new Triangle(1,2,3);
String type = t.computeType();
assertEqual(type, ‘SCALENE’);
}
Parent 2
@Test
public void test(){
Triangle t = new Triangle(3,2,1);
boolean flag = t.isTriangle();
assertTrue(flag);
}
Single-Point Crossover
Genetic Algorithms

17. 17
Test Case
Selection
Initial
Tests
Search
Test
Execution
Variants
Generation
Parent 1
@Test
public void test(){
Triangle t = new Triangle(1,2,3);
boolean flag = t.isTriangle();
assertTrue(flag);
}
Parent 2
@Test
public void test(){
Triangle t = new Triangle(3,2,1);
String type = t.computeType();
assertEqual(type, ‘SCALENE’);
}
Single-Point Crossover
Genetic Algorithms

18. 18
Test Case
Selection
Initial
Tests
Search
Test
Execution
Variants
Generation
Offspring 1
@Test
public void test(){
Triangle t = new Triangle(1,2,3);
boolean flag = t.isRightAngle();
assertTrue(flag); //assertion updated
}
Offspring 2
@Test
public void test(){
Triangle t = new Triangle(3,5,1);
String type = t.computeType();
assertEqual(type, ‘SCALENE’);
Single-Point Crossover
Uniform Mutation
Genetic Algorithms

19. 19
Too Many Paths?
1
25
6 7 3
98
10
4
Control Flow Graph
Even small program have multiple paths:
<1, 2, 4, 10>
<1, 2, 3, 10>
<1, 5, 7, 9, 10>
<1, 5, 6, 10>
Obj. Function 1
Obj. Function 2
Obj. Function 3
Obj. Function 4
How can we solve multiple-paths
(many-functions) in the same time?

20. How to Solve Multiple
Targets?
20

21. 21
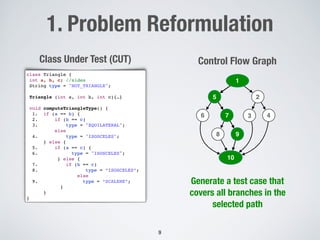
Single Target Approach
1
25
6 7 3
98
10
4
Control Flow Graph TestSuite = {}
For each uncovered target {
[Fit,Test] = GeneticAlgorithm(target)
If (Fit == 0)
TestSuite = TestSuite + Test
}
return(TestSuite)
Limitations:
1) In which order should we select the targets?
2) Some targets are more difficult than other
(how to split the time?)
3) Infeasible paths?

22. 22
Linear Independent Path-Based Search (LIPS)
Key Ingredients:
1) Use the tests from previous GA runs as
starting test for the next GA runs
2) Select the last branches in independent
paths as targets
3) Dynamic budget re-allocation
1
25
6 7 3
98
10
4
Scalabrino et al. SSBSE 2016
Targets to
optimize first

23. 23
Many-Objective Sorting Algorithms (MOSA)
b1 = |a-0|
Example:
b2 = |a-1|
b3 = |a+1|
example(2)
example(0)
example(-2)
Given: B = {b1, . . . , bm} branches of a program.
Find: test cases T = {t1, . . . , tn} minimising the following fitness objectives:
min f1(T) = approach_level(b1) + branch_distance(b1)
min f2(T) = approach_level(b2) + branch_distance(b2)
…
min fm(T) = approach_level(bm) + branch_distance(bm)
String example(int a) {
switch (a) {
case 0 : return “0”;
case 1 : return “1”;
case -1 : return “-1”;
default: return “default”;
}

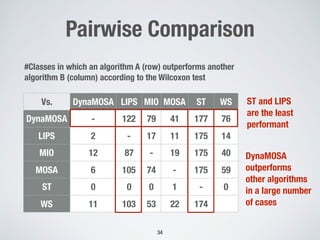
24. 24
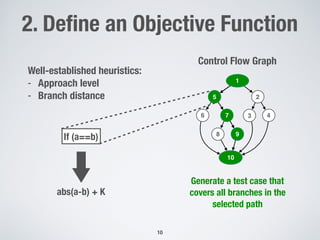
Many-Objective Sorting Algorithms (MOSA)
Objective 1
Objective 2
Not all non-dominated
solutions are optimal for
the purpose of testing
Min
Min
[A. Panichella, F. Kifetew,
P. Tonella ICST 2015]
Pareto
Front
These points are
better than others

25. 25
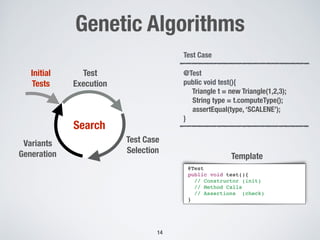
DynaMOSA: Dynamic MOSA
1
25
6 7 3
98
10
4
Control Flow Graph
Rationale:
• Not all branches (objectives) are
independent from one another
• We cannot cover branch <3,10> without
covering <2,3>
Idea:
• Organize targets in levels based on their
structural dependencies
• Start the search with the first-level
targets, then optimize the second level,
and so on
1* Level
2* Level
3* Level
[A. Panichella, F. Kifetew,
P. Tonella, TSE 2018]

26. 26
Many Independent Objective (MIO)
MIO is a co-evolutionary algorithms:
• Different Islands/populations
• One Island for each target
• Test cases within the same island are
ranked exclusively according to the
function for the corresponding target
• Islands associated to probably
infeasible targets are ignored during the
evolution
1
25
6 7 3
98
10
4
<1,5> <1,2>
<5,6>
…
Island
Test Case
Target

27. 27
Whole-Suite Approach (WSA)
A solution is a test suite rather than a test
cases (different granularity level)
Test Suite
Test Case
Fitness Function = Sum of all branch
distances
Crossover = Switching test cases between
two test suites
Mutation = add, remove, edit a test case

28. 28
Previous Study Claims
Scalabrino et al.
SSBSE 2016
Roja et al.
EMSE 2017
Panichella et al.
ICST 2015
Panichella et al.
TSE 2018
Arcuri
SSBSE 2017
LIPS more
efficient than
MOSA
Whole-suite
better than
single-target
MOSA is better
than Whole-
suite
DynaMOSA is
better than
MOSA
MIO is as
competitive to
MOSA

29. Need forLarge-scale
Comparison
29

30. 30
http://www.evosuite.org • Command Line
• Eclipse Plugin
• Intellij IDEA plugin
• Maven Plugin
• Measure Code Coverage

31. 31
https://github.com/EvoSuite/evosuite
• Single Target (ST)
• Whole-Suite Approach (WSA)
• MOSA
• DynaMOSA
• MIO
• LIPS
Our
Implementation

32. Benchmark
32
Benchmark:
175 non-trivial classes sampled from SF110
+ 5 largest classes in SF110
Selection Procedure:
• Computing the McCabe’s cyclomatic complexity (MCC)
• Filtering out all trivial classes (having only methods with MCC <5)
• Random sampling from the pruned projects
Search Budget: Three minutes

33. RQ1: How Do the Different Algorithms
Perform in Terms of Code Coverage?
33
# Classes
No Winner
DynaMOSA
MOSA
MIO
WS
Single
LIPS
0 17,5 35 52,5 70

34. Pairwise Comparison
34
Vs. DynaMOSA LIPS MIO MOSA ST WS
DynaMOSA - 122 79 41 177 76
LIPS 2 - 17 11 175 14
MIO 12 87 - 19 175 40
MOSA 6 105 74 - 175 59
ST 0 0 0 1 - 0
WS 11 103 53 22 174
#Classes in which an algorithm A (row) outperforms another
algorithm B (column) according to the Wilcoxon test
DynaMOSA
outperforms
other algorithms
in a large number
of cases
ST and LIPS
are the least
performant

35. Friedman’s Test
35
ID Meta-heuristics Ranking Statistically better than
(1) DynaMOSA 2.05 2, 3, 4, 5, 6
(2) MOSA 2.63 3, 4, 5, 6
(3) WSA 3.10 4, 5, 6
(4) MIO 3.24 5, 6
(5) LIPS 4.10 6
(6) ST 5.87 -
Results of the Friedman test
(p-value = 3.79 x 10-10)

36. RQ2: How Do the Different Algorithms
Perform Over Time?
36
Coverage
Time
Algorithm 1
Algorithm 2
The final coverage tells only
part of the story
Two algorithm may perform
differently over time even if
they reach the same final
coverage
Let’s use the Area Under the
Chart (AUC) as metric

37. 37
# Classes
No Winner
DynaMOSA
MOSA
MIO
WS
Single
LIPS
0 30 60 90 120
RQ2: How Do the Different Algorithms
Perform Over Time?

38. Friedman’s Test
38
ID Meta-heuristics Ranking Statistically better than
(1) DynaMOSA 1.71 2, 3, 4, 5, 6
(2) MOSA 2.46 3, 4, 5, 6
(3) WSA 2.77 4, 5, 6
(4) MIO 3.99 5, 6
(5) LIPS 4.21 6
(6) ST 5.85 -
Results of the Friedman test
(p-value = 1.14 x 10-12)

39. RQ3: Does the Class Size Affect the
Performance of the Different Algorithms?
39
Rank Approach Statistically better than
(1) 1.71 DynaMOSA (2), (3), (4), (5), (6)
(2) 2.46 MOSA (3), (4), (5), (6)
(3) 2.77 MIO (4), (5), (6)
(4) 3.99 WSA (5), (6)
(5) 4.21 LIPS (6)
(6) 5.85 ST -
DynaMOSA
MOSA
MIO
WSA
LIPS
ST
27
32
47
67
82
125
190
353
7938
#Branch
0.00
0.20
0.40
0.60
0.80
1.00
BranchCoverage
Figure 5: Heatmap showing the interaction between branch coverage a

40. 40
Previous Study Claims
Scalabrino et al.
SSBSE 2016
Roja et al.
EMSE 2017
Panichella et al.
ICST 2015
Panichella et al.
TSE 2018
Arcuri
SSBSE 2017
LIPS more
efficient than
MOSA
Whole-suite
better than
single-target
MOSA is better
than Whole-
suite
DynaMOSA is
better than
MOSA
MIO is as
competitive to
MOSA
Approved Approved ApprovedApproved
Not
Approved

41. Demo
41

42. 42
More Studies
A. Panichella, F. Kifetew, P. Tonella (IST 2018) J. Campos et al. (IST 2018)
Confirm our Results

43. AI-Based Testing at TUDelft
43
https://github.com/STAMP-project/botsing https://github.com/SERG-Delft/evosql
https://github.com/apanichella/evosuite https://github.com/dappelt/xavier-grammar

44. Testing Selft-Driving Cars
44

45. Automated Test Generation for
Unit Testing and Beyond
Annibale Panichella
a.panichella@tudelf.nl
@AnniPanic
45