Download as PDF, PPTX
Uploaded byAnnibale Panichella
Incremental Control Dependency Frontier Exploration for Many-Criteria Test Case Generation
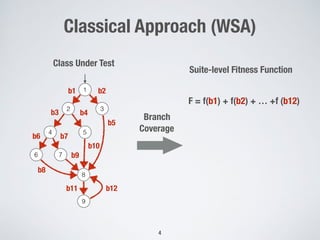
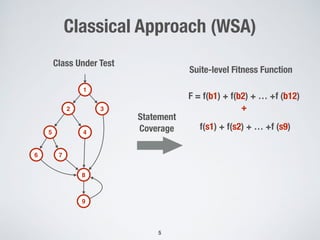
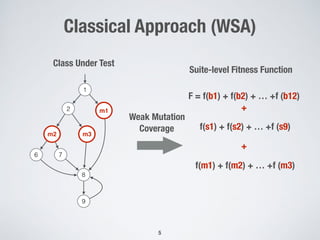
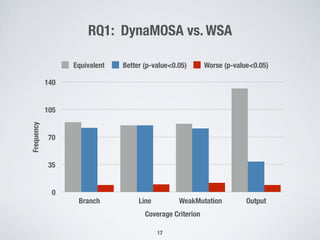
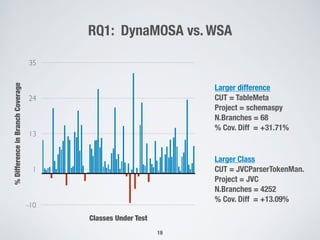
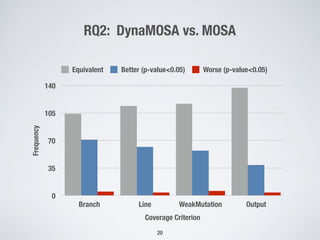
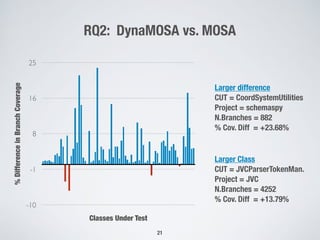
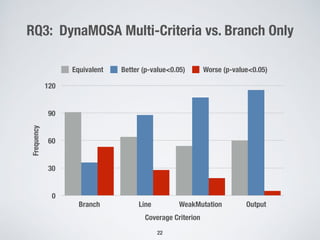
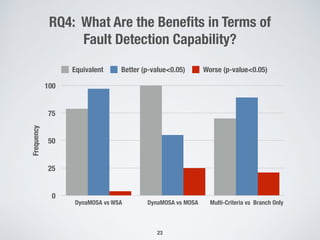
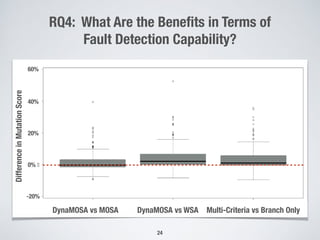
The document presents a method for many-criteria test case generation using incremental control dependency frontier exploration, optimizing several criteria simultaneously without increasing computational costs. It discusses the enhancements over classical approaches through dynamic many-objective sorting algorithms that address multi-criteria coverage effectively. Empirical studies demonstrate the proposed method's superiority in branch coverage and fault detection capabilities over traditional approaches.
More Related Content
Similar to Incremental Control Dependency Frontier Exploration for Many-Criteria Test Case Generation
Incremental Control Dependency Frontier Exploration for Many-Criteria Test Case Generation
- 1. Incremental Control DependencyFrontier Exploration for Many-Criteria Test Case Generation Annibale Panichella, Fitsum M. Kifetew, Paolo Tonella September 11, 2017 !1
- 2. Background Rojas et al.SSBSE 2015 "Optimising for several criteria at the same time is feasible without increasing computational costs" !2
- 3. Classical Approach (WSA) 1 23 4 5 8 Class Under Test 7 9 6 Suite-level Fitness Function 3
- 4. Classical Approach (WSA) 1 23 4 5 8 7 9 6 Suite-level Fitness Function Branch Coverage b2b1 b3 b4 b5 b6 b7 b8 b9 b10 b11 b12 F = f(b1) + f(b2) + … +f (b12) Class Under Test 4
- 5. Classical Approach (WSA) Suite-levelFitness Function Statement Coverage F = f(b1) + f(b2) + … +f (b12) + f(s1) + f(s2) + … +f (s9) 1 2 3 5 4 8 7 9 6 Class Under Test 5
- 6. Classical Approach (WSA) Suite-levelFitness Function Weak Mutation Coverage F = f(b1) + f(b2) + … +f (b12) + f(s1) + f(s2) + … +f (s9) f(m1) + f(m2) + … +f (m3) + 1 2 m1 m2 m3 8 7 9 6 Class Under Test 5
- 7.
- 8. Enhanced Control FlowGraph 6 Annibale Panichella1 , Fitsum Meshesha Kifetew2 , and Paolo Tonella3 (a) Example program (b) Single criterion (c) Multiple criteria Fig. 1. Code (left), CDG (middle), and ECDG (right) of an example program Algorithm 1: MC-DynaMOSA Input: B = {⌧1, . . . , ⌧m} the set of coverage targets of a program. CDG = hN, E, si: control dependency graph of the program Result: A test suite T L1 L2 L5 L3 b1 b4 b2 b3 L6 L7 L8 b5 b6 b0 Control Flow Graph Branches + Statements 7
- 9. Enhanced Control FlowGraph 6 Annibale Panichella1 , Fitsum Meshesha Kifetew2 , and Paolo Tonella3 (a) Example program (b) Single criterion (c) Multiple criteria Fig. 1. Code (left), CDG (middle), and ECDG (right) of an example program Algorithm 1: MC-DynaMOSA Input: B = {⌧1, . . . , ⌧m} the set of coverage targets of a program. CDG = hN, E, si: control dependency graph of the program Result: A test suite T L1 L2 L5 b1 b4 b2 L7 L8 b5 b6 b0 Enhanced CFG L3, μ1 L6, μ2 Branches + Statements + + Weak Mutation b3 8
- 10. Enhanced Control FlowGraph 6 Annibale Panichella1 , Fitsum Meshesha Kifetew2 , and Paolo Tonella3 (a) Example program (b) Single criterion (c) Multiple criteria Fig. 1. Code (left), CDG (middle), and ECDG (right) of an example program Algorithm 1: MC-DynaMOSA Input: B = {⌧1, . . . , ⌧m} the set of coverage targets of a program. CDG = hN, E, si: control dependency graph of the program Result: A test suite T L1 L2 L5 b1 b4 b2 L7 b5 b6 b0 Enhanced CFG L3, μ1 L6, μ2// o2: x<0, o3: x>0,… L8, o1, o2 Branches + Statements + Weak Mutation + Output Diversity b3 9
- 11. Dynamic Many-Objective SortingAlgorithm for Multi-Criteria Coverage L1 L2 L5 b1 b4 b2 L7 b5 b6 b0 L3, μ1 L6, μ2 L8, o1, o2 b3 Status Current Objectives Covered Targets Init. {b0} 10
- 12. Dynamic Many-Objective SortingAlgorithm for Multi-Criteria Coverage L1 L2 L5 b1 b4 b2 L7 b5 b6 b0 L3, μ1 L6, μ2 L8, o1, o2 b3 Status Current Objectives Covered Targets Init. {b0} b0 covered {b1, b5} {b0, L1} 11
- 13. Dynamic Many-Objective SortingAlgorithm for Multi-Criteria Coverage L1 L2 L5 b1 b4 b2 L7 b5 b6 b0 L3, μ1 L6, μ2 L8, o1, o2 b3 11 f(b1) f(b5)
- 14. Dynamic Many-Objective SortingAlgorithm for Multi-Criteria Coverage L1 L2 L5 b1 b4 b2 L7 b5 b6 b0 L3, μ1 L6, μ2 L8, o1, o2 b3 11 f(b1) f(b5) T1 T2 T3 T4
- 15. Dynamic Many-Objective SortingAlgorithm for Multi-Criteria Coverage L1 L2 L5 b1 b4 b2 L7 b5 b6 b0 L3, μ1 L6, μ2 L8, o1, o2 b3 Status Current Objectives Covered Targets Init. {b0} b0 covered {b1, b5} {b0, L1} b1 covered {b2, b3, b5} {b0, L1, b1, L2} 12
- 16. Dynamic Many-Objective SortingAlgorithm for Multi-Criteria Coverage L1 L2 L5 b1 b4 b2 L7 b5 b6 b0 L3, μ1 L6, μ2 L8, o1, o2 b3 Status Current Objectives Covered Targets Init. {b0} b0 covered {b1, b5} {b0, L1} b1 covered {b2, b3, b5} {b0, L1, b1, L2} b5 covered {b2, b3, µ2, b4, b6} {b0, L1, b1, L2, b5, L6} 13
- 17. Dynamic Many-Objective SortingAlgorithm for Multi-Criteria Coverage L1 L2 L5 b1 b4 b2 L7 b5 b6 b0 L3, μ1 L6, μ2 L8, o1, o2 b3 Status Current Objectives Covered Targets Init. {b0} b0 covered {b1, b5} {b0, L1} b1 covered {b2, b3, b5} {b0, L1, b1, L2} b5 covered {b2, b3, µ2, b4, b6} {b0, L1, b1, L2, b5, L6} b2 covered {b3, b4, b6} {b0, L1, b1, L2, b5, L6, b2, L3, µ1, µ2} b3 covered {b4, b6} {b0, L1, b1, L2, b5, L6, b2, L3, µ1, µ2, b3, L5} 14
- 18.
- 19. Study Context Benchmark: 180 non-trivialclasses sampled from SF110 Selection Procedure: • Computing the McCabe’s cyclomatic complexity (MCC) • Filtering out all trivial classes (having only methods with MCC <5) • Random sampling from the pruned projects Search Budget: Three minutes 16
- 20. RQ1: DynaMOSA vs.WSAFrequency 0 35 70 105 140 Coverage Criterion Branch Line WeakMutation Output Equivalent Better (p-value<0.05) Worse (p-value<0.05) 17
- 21. DynaMOSA is better thanWSA WSA is better than DynaMOSA RQ1: DynaMOSA vs. WSA %DifferenceinBranchCoverage -50 -38 -25 -13 0 13 25 38 50 Classes Under Test 18
- 22. RQ1: DynaMOSA vs.WSA %DifferenceinBranchCoverage -10 1 13 24 35 Classes Under Test Larger difference CUT = TableMeta Project = schemaspy N.Branches = 68 % Cov. Diff = +31.71% Larger Class CUT = JVCParserTokenMan. Project = JVC N.Branches = 4252 % Cov. Diff = +13.09% 19
- 23. RQ2: DynaMOSA vs.MOSAFrequency 0 35 70 105 140 Coverage Criterion Branch Line WeakMutation Output Equivalent Better (p-value<0.05) Worse (p-value<0.05) 20
- 24. RQ2: DynaMOSA vs.MOSA %DifferenceinBranchCoverage -10 -1 8 16 25 Classes Under Test Larger difference CUT = CoordSystemUtilities Project = schemaspy N.Branches = 882 % Cov. Diff = +23.68% Larger Class CUT = JVCParserTokenMan. Project = JVC N.Branches = 4252 % Cov. Diff = +13.79% 21
- 25. RQ3: DynaMOSA Multi-Criteriavs. Branch OnlyFrequency 0 30 60 90 120 Coverage Criterion Branch Line WeakMutation Output Equivalent Better (p-value<0.05) Worse (p-value<0.05) 22
- 26. RQ4: What Arethe Benefits in Terms of Fault Detection Capability?Frequency 0 25 50 75 100 DynaMOSA vs WSA DynaMOSA vs MOSA Multi-Criteria vs Branch Only Equivalent Better (p-value<0.05) Worse (p-value<0.05) 23
- 27. RQ4: What Arethe Benefits in Terms of Fault Detection Capability? DynaMOSA vs MOSA DynaMOSA vs WSA Multi-Criteria vs Branch Only DifferenceinMutationScore 60% 40% 20% 0% -20% 24
- 28. What EAs toChoose? Even Larger
- 29. Incremental Control DependencyFrontier Exploration for Many-Criteria Test Case Generation Annibale Panichella, Fitsum M. Kifetew, Paolo Tonella September 11, 2017