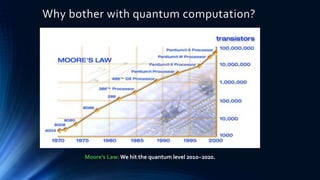
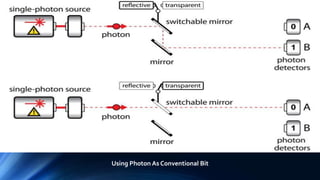
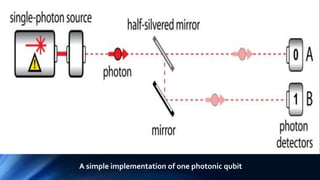
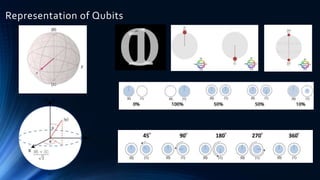
Quantum computing uses the principles of quantum mechanics to perform calculations. Richard Feynman first proposed the idea in 1982. Major developments include David Deutsch developing the quantum turing machine in 1985, and Peter Shor creating an algorithm to factor large numbers in polynomial time in 1994. Quantum computers represent data using qubits which can be in superposition of both 0 and 1 states, allowing exponentially more information to be processed than classical computers. Potential applications include machine learning, genomics, chemistry, materials science, cryptography, and defense.

1. Quantum Computing
INTRODUCTION
By Muhammad Miqdad Khan

2. What is Quantum Computing?
 A quantum computer is a machine that performs calculations based
on the laws of quantum mechanics, which is the behavior of particles
at the sub-atomic level.

3.  “I think I can safely say that nobody understands
quantum mechanics” - Feynman
 1982 - Feynman proposed the idea of creating
machines based on the laws of quantum mechanics
instead of the laws of classical physics.
History
1985 - David Deutsch developed the quantum turing machine, showing that quantum
circuits are universal.
 1994 - Peter Shor came up with a quantum algorithm to factor very large numbers in
polynomial time.
1997 - Lov Grover develops a quantum search algorithm with O(√N) complexity

4. Why bother with quantum computation?
Moore’s Law:We hit the quantum level 2010~2020.

5. The design of devices on such a small scale will require engineers to control
quantum mechanical effects.
Allowing computers to take advantage of quantum mechanical
behaviour allows us to do more than cram increasingly many
microscopic components onto a silicon chip…
… it gives us a whole new framework in which information can be
processed in fundamentally new ways.
The nineteenth century was known as the machine age, the twentieth century will go down in history as the
information age. I believe the twenty-first century will be the quantum age. Paul Davies, Professor Natural
Philosophy – Australian Centre for Astrobiology

6. Representation of Data - Qubits
• A bit of data is represented by a single atom that is in one of two
states denoted by |0> and |1>. A single bit of this form is known as a
qubit
∣ψ⟩ = α∣0⟩ + β∣1⟩
The probability that the qubit will be measured in the
state ∣0⟩ is ∣α∣2 and the probability that it will be
measured in the state ∣1⟩ is ∣β∣2. Hence the total
probability of the system being observed in either
state ∣0⟩ or ∣1⟩ is 1.
𝑵 𝑸𝒖𝒃𝒊𝒕𝒔 = 𝟐 𝑵
of Classical Bits

7. Using Photon As Conventional Bit

8. A simple implementation of one photonic qubit

9. Representation of Qubits

10. Applications
• Machine Learning
• Genomics Sequencing
• Chemical Information
• Drugs Making
• True Random Number Generation
• Security
• Cryptography
• Defense