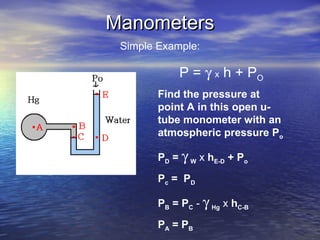
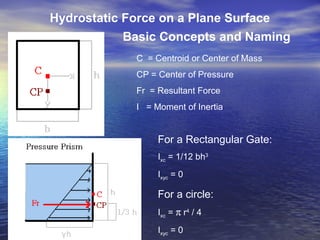
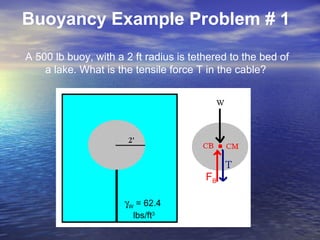
Fluid mechanics concepts including pressure, atmospheric pressure, fluid statics, hydrostatics, and buoyancy are introduced. Pressure increases linearly with depth in static fluids and can produce large forces on surfaces like dams. The pressure at a point depends on the density of the fluid and the depth. Buoyancy forces allow objects to float based on the weight and volume of fluid displaced.

1. Introduction to Fluid MechanicsIntroduction to Fluid Mechanics
Dr. BedientDr. Bedient
Civil and Environmental EngineeringCivil and Environmental Engineering
CEVE 101

2. Fluids:Fluids:
Statics vs DynamicsStatics vs Dynamics

3. Atmospheric PressureAtmospheric Pressure
Pressure = Force per Unit Area
Atmospheric Pressure is the weight of the
column of air above a unit area. For example,
the atmospheric pressure felt by a man is the
weight of the column of air above his body
divided by the area the air is resting on
P = (Weight of column)/(Area of base)
Standard Atmospheric Pressure:
1 atmosphere (atm)
14.7 lbs/in2
(psi)
760 Torr (mm Hg)
1013.25 millibars = 101.3 kPascals
1kPa = 1Nt/m2

4. Fluid StaticsFluid Statics
Basic Principles:
 Fluid is at rest : no shear forces
 Pressure is the only force acting
What are the forces acting on the
block?
 Air pressure on the surface - neglect
 Weight of the water above the block
 Pressure only a function of depth

5. UnitsUnits
SI - International System
Length Meter
Time Sec
Mass Kg
Temp 0
K = 0
C + 273.15
Force Newton = Nt = 1 kg m / s2
Gravity 9.81 m/s2
Work = Fxd Joule = Nt-m
Power = F/t Watt = Joule/sec

6. UnitsUnits
English Length in Ft
Time in Sec
lbm (slug) - 1 slug = 32.2 lbm
Force - lb
Gravity - 32.2 ft/sec2
Work = slug-ft/s2

7. Properties of FluidsProperties of Fluids
Density = ρ (decreases with rise in T)
 mass per unit volume ( lbs/ft3
or kg/m3
)
for water density = 1.94 slugs/ft3
or 1000 kg/m3
Specific Weight = γ (Heaviness of fluid)
 weight per unit volume γ = ρg
for water spec wt = 62.4 lbs/ft3
or 9.81 kN/m3
Specific Gravity = SG
 Ratio of the density of a fluid to the density of water
SG = ρf / ρw SG of Hg = 13.55

8. Ideal Gas Law relates pressure to Temp for a gas
P = ρRT
T in 0
K units
R = 287 Joule / Kg-0
K
Pressure
Force per unit area:
lbs/in2
(psi), N/m2
, mm Hg, mbar or atm
1 Nt/m2 = Pascal = Pa
Std Atm P = 14.7 psi = 101.33 kPa = 1013 mb
Viscosity fluid deforms when acted on by shear
stress
µ = 1.12 x 10-3
N-s/m2
Surface tension - forces between 2 liquids or gas
and liquid - droplets on a windshield.

9. Section 1: PressureSection 1: Pressure
Pressure at any point in a static fluid not fcn of x,y,or z
Pressure in vertical only depends on γ of the fluid
P = γh + Po
Gage pressure: relative to
atmospheric pressure: P = γh
Thus for h = 10 ft, P = 10(62.4) =
624 psf
This becomes 624/144 = 4.33 psi
P = 14.7 psi corresponds to 34 ft
10 ft

10. What is the pressure at point A? At point B?
γG = 42.43 lbs/ft3
SG = 0.68
γW = 62.4 lbs/ft3
At point A: PA = γG x hG + PO
= 42.43 x 10 + PO
424.3 lbs/ft2
gage
At point B: PB = PA + γW x hW
= 424.3 + 62.4 x 3
611.5 lbs/ft2
gage
Converting PB to psi:
(611.5 lbs / ft2
) / (144 in2
/ft2
)
= 4.25 psi
Pressure in a Tank Filled with Gasoline and Water

11. Measurement of PressureMeasurement of Pressure
Barometer (Hg) - Toricelli 1644
Piezometer Tube
U-Tube Manometer - between two points
Aneroid barometer - based on spring
deformation
Pressure transducer - most advanced
QuickTime™ and aTIFF (LZW) decompressorare needed to see this picture.

12. Manometers - measureManometers - measure ∆∆PP
Rules of thumb:
 When evaluating, start from the known
pressure end and work towards the
unknown end
 At equal elevations, pressure is
constant in the SAME fluid
 When moving down a monometer,
pressure increases
 When moving up a monometer,
pressure decreases
 Only include atmospheric pressure on
open ends

13. ManometersManometers
Find the pressure at
point A in this open u-
tube monometer with an
atmospheric pressure Po
PD = γ W x hE-D + Po
Pc = PD
PB = PC - γ Hg x hC-B
PA = PB
Simple Example:
P = γ x h + PO

14. For a fluid at rest, pressure increases linearly with depth. As aFor a fluid at rest, pressure increases linearly with depth. As a
consequence, large forces can develop on plane and curved surfaces.consequence, large forces can develop on plane and curved surfaces.
The water behind the Hoover dam, on the Colorado river, isThe water behind the Hoover dam, on the Colorado river, is
approximately 715 feet deep and at this depth the pressure is 310 psi.approximately 715 feet deep and at this depth the pressure is 310 psi.
To withstand the large pressure forces on the face of the dam, itsTo withstand the large pressure forces on the face of the dam, its
thickness varies from 45 feet at the top to 660 feet at the base.thickness varies from 45 feet at the top to 660 feet at the base.
Section 2: HydrostaticsSection 2: Hydrostatics
And the Hoover Dam

15. Hydrostatic Force on a Plane Surface
Basic Concepts and Naming
Pressure = γ h
γ = spec gravity of water
h = depth of water
C = Center of Mass of Gate
CP = Center of Pressure on Gate
Fr = Resultant Force acts at CP
γh

16. Hydrostatic Force on a Plane Surface
Basic Concepts and Naming
C = Centroid or Center of Mass
CP = Center of Pressure
Fr = Resultant Force
I = Moment of Inertia
γh
For a Rectangular Gate:
Ixc = 1/12 bh3
Ixyc = 0
For a circle:
Ixc = π r4
/ 4
Ixyc = 0

17. Hydrostatic Force on a Plane Surface
The Center of Pressure YR lies below the centroid - since pressure
increases with depth
FR = γ A YC sinθ
or FR = γ A Hc
YR = (Ixc / YcA) + Yc
XR = (Ixyc / YcA) + Xc
but for a rectangle or circle:
XR = Xc
For 90 degree walls:
FR = γ A Hc

18. Hydrostatics Example Problem # 1
What is the Magnitude and Location of the
Resultant force of water on the door?
γW = 62.4 lbs/ft3
Water Depth = 6 feet
Door Height = 4 feet
Door Width = 3 feet

19. Hydrostatics Example Problem #1
Magnitude of Resultant
Force:
FR = γW A HC
FR = 62.4 x 12 x 4 = 2995.2 lbs
Important variables:
HC and Yc = 4’
Xc = 1.5’
A = 4’ x 3’ = 12’
Ixc = (1/12)bh3
= (1/12)x3x43
= 16 ft4
Location of Force:
YR = (Ixc / YcA) + Yc
YR = (16 / 4x12) + 4 = 4.333 ft down
XR = Xc (symmetry) = 1.5 ft from the
corner of the door

20. Section 3: Buoyancy
Archimedes Principle: Will it Float?
The upward vertical force felt by a submerged, or partially submerged,
body is known as the buoyancy force. It is equal to the weight of the
fluid displaced by the submerged portion of the body. The buoyancy
force acts through the centroid of the displaced volume, known as the
center of buoyancy. A body will sink until the buoyancy force is equal to
the weight of the body.
FB = γ x Vdisplaced
= Vdisp
FB
FB
W = FB
FB = γW x Vdisp

21. Buoyancy Example Problem # 1
A 500 lb buoy, with a 2 ft radius is tethered to the bed of
a lake. What is the tensile force T in the cable?
γW = 62.4
lbs/ft3
FB

22. Buoyancy Example Problem # 1
Displaced Volume of Water:
Vdisp-W = 4/3 x π x R3
Vdisp-W = 33.51 ft3
Buoyancy Force:
FB = γW x Vdisp-w
FB = 62.4 x 33.51
FB = 2091.024 lbs up
Sum of the Forces:
ΣFy = 0 = 500 - 2091.024 + T
T = 1591.024 lbs down

23. Will It Float?
Ship Specifications:
Weight = 300 million pounds
Dimensions = 100’ wide by 150’ tall by 800’ long
Given Information: γW = 62.4 lbs/ft3

24. Assume Full Submersion:
FB = Vol x γW FB = (100’ x 150’ x 800’) x 62.4 lbs/ft3
FB
= 748,800,000 lbs
Weight of Boat = 300,000,000 lbs
The Force of Buoyancy is greater than the Weight of the Boat
meaning the Boat will float!
How much of the boat will be submerged?
Assume weight = Displaced Volume
WB = FB
300,000,000 = (100’ x H’ x 800’) x 62.4 lbs/ft3
H = Submersion depth = 60.1 feet