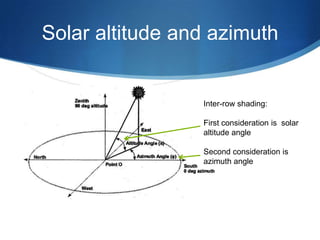
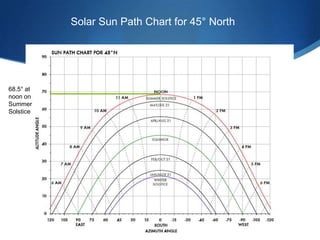
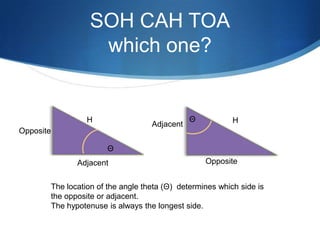
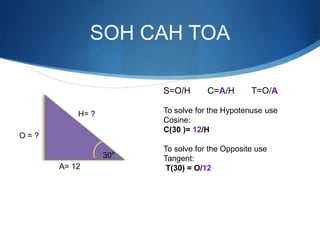
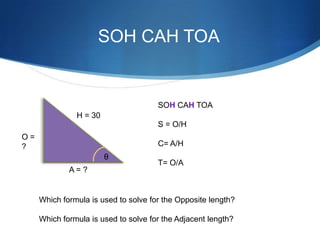
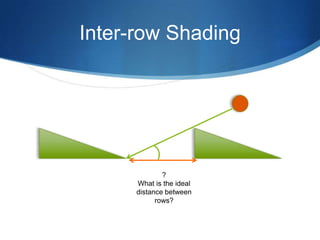
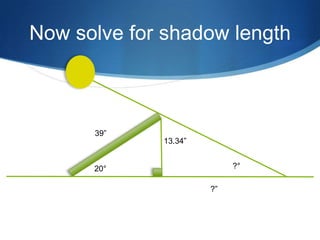
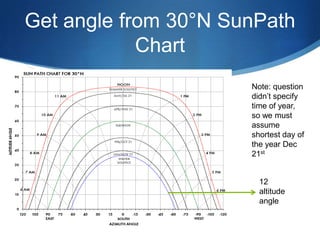
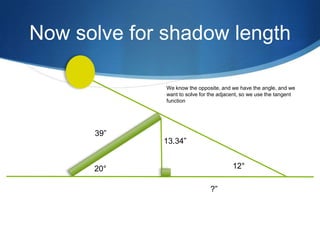
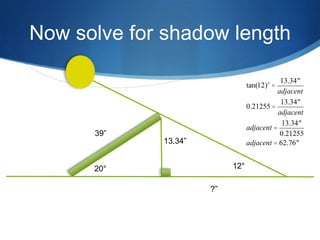
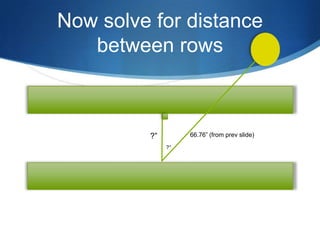
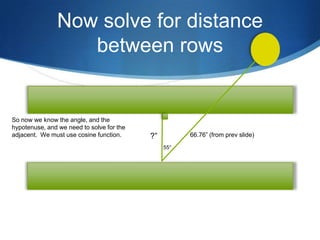
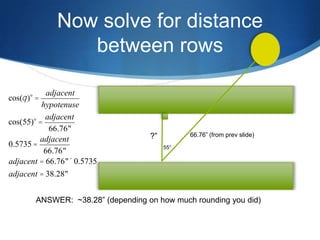
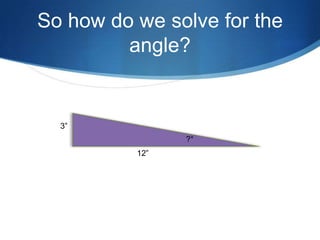
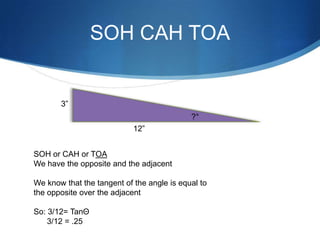
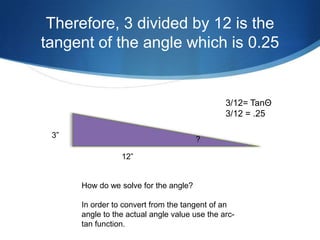
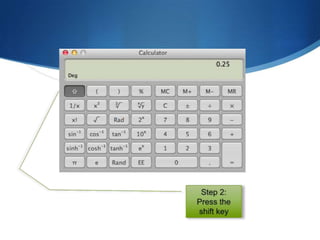
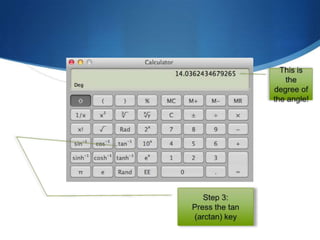
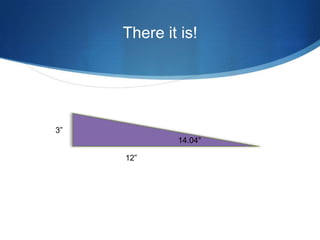
The document details advanced concepts for calculating inter-row shading in solar design, focusing on solar altitude and azimuth angles. It includes the use of trigonometric functions to determine the height and distance needed to avoid shading in solar panel installations. Additionally, practical examples illustrate how to apply these calculations for specific conditions, such as latitude and time of year.

1. Inter-row Shading
Advanced Site Survey Concepts
S

2. Inter-row Shading
S Altitude and Azimuth Angles
S Solar Sun Path Chart
S Trigonometry- SOH CAH TOA
S Application of concepts to problem sets
S Arc-tan function
S Designing on a sloped roof

3. Solar Azimuth and Altitude
angles
There are two primary numbers provided by the solar sun
path chart that are required to do inter row shading
calculations: solar altitude angle and solar azimuth angle.
Solar altitude is how high in the sky the sun is in relation to
the horizon.
Solar azimuth is where the sun is in the sky in relation to a
reference direction, usually south for solar applications.

4. Solar altitude and azimuth
Inter-row shading:
First consideration is solar
altitude angle
Second consideration is
azimuth angle

5. A Simple real world graphic

6. Solar Sun Path Chart for 30° N
84° at
noon on
June
21st-
Summer 11am on
Solstice April 21 and
Aug 21- 66°
3pm on April
36° at 21 and Aug
noon 21- 44°
Dec
21st- Also- 1:20pm
Winter on Feb and
Solstice Oct- 44°

7. Solar Sun Path Chart for 45° North
68.5° at
noon on
Summer
Solstice

8. How do I get my very own Solar
Sun Path Chart?
S http://solardat.uoregon.edu/SunChartProgram.php
S Enter negative for Southern hemisphere (or to cheat
on the Azimuth degree line)

9. What else do we need to know to
design an array that avoids inter-row
shading?
Trigonometry

10. Basic Trig

11. SOH CAH TOA
which one?
H Θ H
Adjacent
Opposite
Θ
Adjacent Opposite
The location of the angle theta (Θ) determines which side is
the opposite or adjacent.
The hypotenuse is always the longest side.

12. SOH CAH TOA

13. SOH CAH TOA
S=O/H C=A/H T=O/A
H= ? To solve for the Hypotenuse use
Cosine:
C(30 )= 12/H
O=?
To solve for the Opposite use
30° Tangent:
A= 12 T(30) = O/12

14. SOH CAH TOA
SOH CAH TOA
H = 30
S = O/H
O=
? C= A/H
θ
T= O/A
A= ?
Which formula is used to solve for the Opposite length?
Which formula is used to solve for the Adjacent length?

15. Which formula is used to solve for
the Opposite length?
SOH CAH TOA
Angle θ = 30°
S = O/H
S(30) = O/30
.5 = O/30
(.5) x 30 = (O/30) x 30
15 = O

16. Which formula would be used to solve for
the Adjacent length?
SOH CAH TOA
Angle θ = 30°
C(30) = A/30
.867= A/30
(.867) x 30 = (A/30) x 30
26.01 = A

17. Next- application to inter-row
shading formula

18. Inter-row Shading
?
What is the ideal
distance between
rows?

19. Question
S You are designing a ground mount PV array at 30°N
Latitude with multiple rows that faces true south. The tilt
of the modules are 20°. The width of the modules are 39
inches and they will be installed in landscape layout.
What is the closest distance the rows of the modules can
be and not cause any shade during the hours of 8AM and
4PM solar time?

20. 1 st Step Determine Height of
back of module
We have the
angle theta, and
we have the
39” hypotenuse, and
? we need to know
the opposite, so
we should use
20° the sine
function…

21. 1 st Step Determine Height of
back of module
opposite
sin(q )° =
hypotenuse
opposite
sin(20)° =
39"
39” opposite
0.34202 =
? 39"
opposite = 39"´ 0.34202
20° opposite = 13.34"

22. Now solve for shadow length
39”
13.34”
20° ?°
?”

23. Get angle from 30°N SunPath
Chart
Note: question
didn’t specify
time of year,
so we must
assume
shortest day of
the year Dec
21st
12
altitude
angle

24. Now solve for shadow length
We know the opposite, and we have the angle, and we
want to solve for the adjacent, so we use the tangent
function
39”
13.34”
20° 12°
?”

25. Now solve for shadow length
13.34"
tan(12)° =
adjacent
13.34"
0.21255 =
adjacent
13.34"
adjacent =
39” 0.21255
13.34” adjacent = 62.76"
20° 12°
?”

26. Now solve for distance
between rows
?” 66.76” (from prev slide)
?°

27. Get azimuth angle from 30°N
SunPath Chart
55°

28. Now solve for distance
between rows
So now we know the angle, and the
hypotenuse, and we need to solve for the
adjacent. We must use cosine function. ?” 66.76” (from prev slide)
55°

29. Now solve for distance
between rows
adjacent
cos(q )° =
hypotenuse
adjacent
cos(55)° =
66.76"
?” 66.76” (from prev slide)
adjacent
0.5735 = 55°
66.76"
adjacent = 66.76"´ 0.5735
adjacent = 38.28"
ANSWER: ~38.28” (depending on how much rounding you did)

30. First we must understand what
3/12 means

31. It refers to the rise over the run
3”
12”
For every 3” of rise, there is 12” of run

32. So how do we solve for the
angle?
3”
?°
12”

33. SOH CAH TOA
3”
?°
12”
SOH or CAH or TOA
We have the opposite and the adjacent
We know that the tangent of the angle is equal to
the opposite over the adjacent
So: 3/12= TanΘ
3/12 = .25

34. Therefore, 3 divided by 12 is the
tangent of the angle which is 0.25
3/12= TanΘ
3/12 = .25
3”
?
12”
How do we solve for the angle?
In order to convert from the tangent of an
angle to the actual angle value use the arc-
tan function.

35. to convert from the tangent of an angle to the
actual angle value use the arctan function.

38. There it is!
3”
14.04°
12”