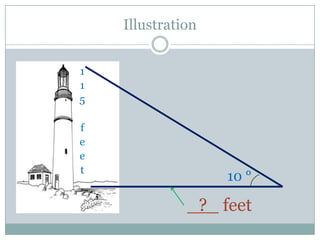
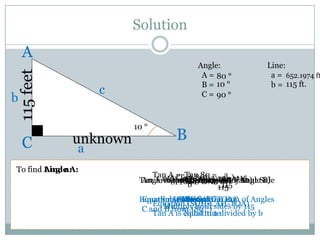
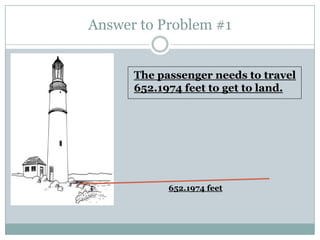
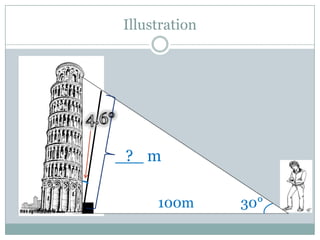
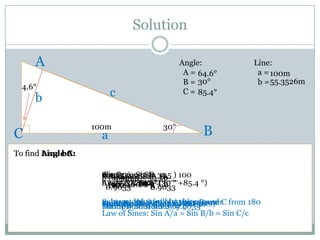
This document contains two trigonometry word problems submitted by Gianne Itaralde to their professor. Problem 1 asks the student to calculate how far a lost boat passenger needs to travel to reach land if they can see a 115-foot lighthouse from their boat at an angle of 10 degrees. The student uses trigonometric functions to determine the distance is 652.1974 feet. Problem 2 asks the student to calculate the height of the Leaning Tower of Pisa if an observer 100 meters from its base measures its angle of elevation as 30 degrees and the tower leans at an angle of 4.6 degrees from vertical. Again using trigonometric functions and the Law of Sines, the

1. Two Problems on the Application
of Fundamentals of Trigonometry
SUBMITTED TO: PROF. LAWAS
SUBMITTED BY: GIANNE ITARALDE
T/TH 9:40-11:10 CLASS

2. Problem #1
A boat with only one passenger is lost at sea. The
passenger, being tired and all, is losing hope that he
might not find land anymore and so, he slept. After a
few hours, he woke up and saw a 115-feet high
lighthouse from a distance.
The angle of elevation from the boat to the top of
the lighthouse is 10°. How far does he need to travel to
get to land?

3. Illustration
1
1
5
f
e
e
t
10 °
_?_ feet

4. Solution
A
Angle: Line:
115 feet
A = 80 ° a = 652.1974 ft
B = 10 ° b = 115 ft.
c C = 90 °
b
10 °
C unknown B
a
To find Angle A:
Line a:
Tan A = _a_ 80= _a_
115 (Tan –180 ==(90 + Angle
Tan
Tan A Angle 652.1974–_a_)°115 Side
= = A =80°A = = C
Angle= Opposite(AngleaAdjacent B)
A a 115 (5.6713)feet 10)
180 Side / a
652.1974 80
Angle
b 115
115
EquationAnswerfor Tan sum of Angles
Equation(SOH-CAH-TOA)
Substitute
(Subtract the 80°
Solve
Multiply
Answer
Equation (SOH-CAH-TOA)
C and Multiply both sides by 115
B from 180 °)
Tan A is equal to a divided by b
Substitute

5. Answer to Problem #1
The passenger needs to travel
652.1974 feet to get to land.
652.1974 feet

6. Problem #2
The leaning tower of Pisa is tilted at an angle of 4.6°
from the vertical. An observer standing 100m from the
base of the tower measures the angle of elevation to be
30°. Find the height of the tower.

7. Illustration
_?_ m
100m 30°

8. Solution
A Angle: Line:
A = 64.6° a = 100m
B = 30° b = 55.3526m
4.6°
b c C = 85.4°
100m 30°
C a B
To find Angle C:
Line b:
A:
10064.6 Sin 50 b
0.9033=== =Sin )0.5
Sin0.9033 0.5= 30 ) 100
b ( ( 0.9033 __50__
Sin A
(0.9033) = B
b 100 A 85.4° (30
Angle C = 90 –-4.6 ° +85.4 °)
= 55.3526m
64.6°
180
0.9033 b b b b
100
a 100 0.9033
b
Solve andSin sum of 90your 30and
Subtract 4.6 ° sidesbe the answer C from 180
Multiply both will and Sin
Solve for both fromLaw°of B
Substitutethatsides by b Sines)
Equationthesides byby 100 answer
Angles
Divide both 64.6
Multiply (Use the 0.9033
Law of Sines: Sin A/a = Sin B/b = Sin C/c

9. Answer to Problem #2
The Leaning Tower of Pisa is
55.3526m high.

10. End of Presentation
GIANNE ITARALDE’S PROJECT FOR FUNTRIG
SOURCES OF IMAGES:
•H T T P : / / S T A T I C . D D M C D N . C O M
•H T T P : / / W W W . D R A G O A R T . C O M
•H T T P : / / D A T A . G R E A T B U I L D I N G S . C O M
•H T T P : / / B O U . M E