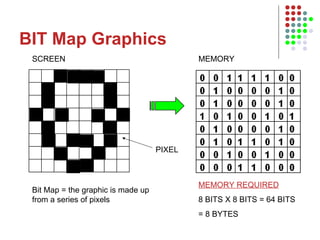
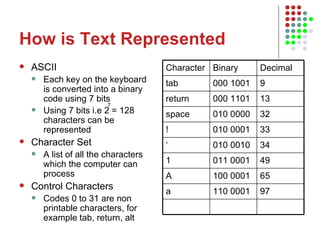
The document outlines the course content for an Intro to Computing course, which is divided into three main units on computer systems, software development, and artificial intelligence. The computer systems unit covers topics such as data representation, computer structure, networking, and representing graphics. Sample lesson plans describe how numbers, text, and images are stored in binary and how floating point numbers are represented using mantissa and exponent.

1. Int 2 Computing Mr Arthur

2. Course Outline 3 Main Units Computer Systems = 40 hours Software Development = 40 hours Artificial Intelligence = 40 hours Assessment 3 End of Unit Assessments (NABS /20) 2 Practical Coursework Tasks (/15 - 30%) Written Exam (/70 or 70%)

3. Computer Systems 5 units in the Computer Systems Section Data Representation = 6 hours Computer Structure = 7 hours Peripherals = 5 hours Networking = 9 hours Computer Software = 9 hours

4. Aims of Lesson 1 How are numbers, text and images represented inside the computer system? Discussing the 2 state computer system Converting positive whole numbers to binary and vice versa Playing Binary Bingo

5. Data Representation 100 billion switches per sq. cm

6. Data Storage Numbers, Text, and Images are all stored as a series of 1s and 0s inside the computer system. These series of 1s and 0s are made up of pulses of electricity from 1 volt to 5 volts

7. Decimal Counting System When we represent numbers we use the decimal counting system, for example 123,000 100,000 10,000 1,000 100 10 1 1 2 3 0 0 0 Since the computer is 2 state, the binary counting system goes up by the power 2, rather than 10 i.e 256 128 64 32 16 8 4 2 1

8. How Positive Whole Numbers are Stored 34 128 64 32 16 8 4 2 1 0 0 1 0 0 0 1 0 = 32 + 2 134 128 64 32 16 8 4 2 1 1 0 0 0 0 1 1 0 = 128 + 4 + 2

9. Binary back to Decimal 1011 0011 128 64 32 16 8 4 2 1 1 0 1 1 0 0 1 1 = 128 + 32 + 16 + 2 + 1 = 179

10. Binary Bingo 42 81 21 16 121 73 101 75 127 128 13 209 32 56 175 192 186 176 121 250 34

11. Aims of Lesson 2 Data Units Bits/Bytes etc Floating Point Representation

12. Storage Capacities 0 or 1 = 1 bit 8 bits = 1 byte 1024 bytes = 1 Kilobyte 1024 Kilobytes = 1 Megabyte 1024 Megabytes = 1 Gigabyte 1024 Gigabytes = 1 Terabyte

13. Representing Non Whole Numbers How do we represent the number 128.75 in binary? 128 + 0.5 + 0.25 = 128.75 128 64 32 16 8 4 2 1 0.5 0.25 0.125 0.0625 1 0 0 0 0 0 0 0 1 1 0 0

14. Mantissa and Exponent Mantissa Exponent 8 8 4 2 1 1 0 0 0 128 64 32 16 8 4 2 1 0.5 0.25 0.125 0.0625 1 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 1 1 0 0

15. Mantissa Exponent 6 8 4 2 1 0 1 1 0 1 0 0 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 0 How do we represent the number 38.125 using floating point 32 16 8 4 2 1 0.5 0.25 0.125 0.0625

16. Representing Non Whole Numbers Mantissa relates to the precision of the number you can represent i.e 34.44454321 Exponent relates to the position of the decimal point 8 4 2 1 0.5 0.25 0.125 0.075 0.0375 0.01875 0.009375

17. Aims of Lesson 3 Representing Graphics Pixels Resolution Graphics Calculations

18. Pixels/Resolution Pixel Stands for Picture Element A pixel is a dot on the screen. It is a graphic segmented up into its simplest form Resolution This is the numbers of pixels there are per inch (dpi) The higher the resolution the higher the quality of the image

19. BIT Map Graphics SCREEN MEMORY PIXEL MEMORY REQUIRED 8 BITS X 8 BITS = 64 BITS = 8 BYTES Bit Map = the graphic is made up from a series of pixels

20. Graphics Resolution The smaller the size of the pixels, the finer the detail of the image 800 x 600 pixels lower quality than 1024 x 768 As the number of pixels increases so does the storage space required Pixel Pattern using 8x8 grid Pixel Pattern using 16x16 grid

21. Calculating Storage Capacities of Bit Mapped Images Storage Requirements = total number of pixels * number of bits used for each pixel This picture of Mr Haggarty has a resolution of 300dpi. The image is 2 inches by 4 inches in 128 colours 300 X 2 = width 600 pixels 300 X 4 = height 1200 pixels Total pixels = 600 X 1200 = 720,000 pixels Each pixel = 7 bits i.e. 2 = 128 colours 720,000 X 7 = 5,040,000 bits / 8 = 630,000 bytes 630,000 / 1024 = 615Kb 7

22. Aims of Lesson 4 Last Lessons Representing whole numbers Decimal to Binary Binary to Decimal Non-whole numbers Floating Point Data Units Representing Graphics Pixels Resolution Graphics Calculations Today’s Lesson Representing Text Advantages of using binary

23. How is Text Represented ASCII Each key on the keyboard is converted into a binary code using 7 bits Using 7 bits i.e 2 = 128 characters can be represented Character Set A list of all the characters which the computer can process Control Characters Codes 0 to 31 are non printable characters, for example tab, return, alt 7 Character Binary Decimal tab 000 1001 9 return 000 1101 13 space 010 0000 32 ! 010 0001 33 ‘ 010 0010 34 1 011 0001 49 A 100 0001 65 a 110 0001 97

24. Binary Message 1010100 1001000 1001001 1010011 0100000 1010111 1000101 1000001 1010100 1001000 1000101 1010010 0100000 1001001 1010011 0100000 1001000 1001111 1010010 1010010 1001001 1000010 1001100 1000101

25. Advantages of Using Binary Computers are 2 state e.g. on and off and Binary is a 2 state counting system e.g. 1010 If there is any drop in voltage (degradation) the pixel etc is still represented as a 1 (black)