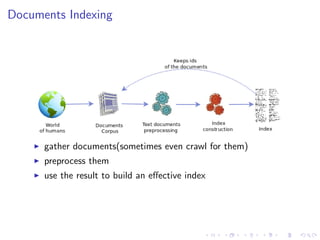
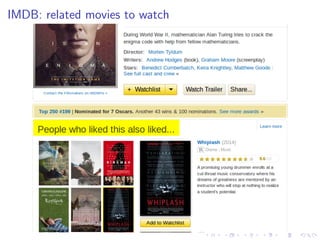
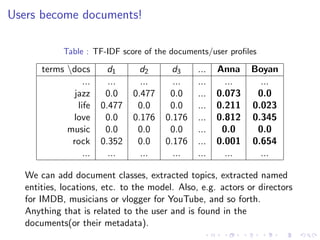
This document provides an introduction to information retrieval and recommender systems. It begins with defining information retrieval as finding documents that satisfy an information need from large collections. It then discusses how documents are indexed and preprocessed, including tokenization, stopwords removal, and lemmatization. Boolean and vector space retrieval models are introduced. The document also defines recommender systems as systems that suggest items of interest to users based on their preferences. It describes collaborative filtering and content-based recommender approaches.

1. From Information Retrieval
to Recommender Systems
Maria Mateva
Sofia University
Faculty of Mathematics and Informatics
Data Science Society
February 25, 2015

2. whoami
Maria Mateva:
BSc of FMI, “Computer Science”
MSc of FMI, “Artificial Intelligence”
2.5 years software developer in Ontotext
1 year software developer in Experian
3 semesters - teaching assistant in “Informarion Retrieval”
now joining Data Science Society

3. Acknowledgements
This lecture is a mixture from knowledge I gained as a teaching
assistant in Information Retrieval in FMI, Sofia University and from
knowledge I gained during research in Ontotext.
Special thanks to:
FMI - in general, always
Doc. Ivan Koychev for letting me be part of his team
Ontotext, especially
PhD Konstantin Kutzkov for our work on recommendations
PhD Laura Tolo¸si for her guidance
Prof. Christopher Manning of Stanford for opening
“Introduction to Information Retrieval” for all of us
Jure Leskovec, Anand Rajaraman, Jeff Ullman for “Mining
Massive Datasets” book and course

4. Today we discuss...
Introduction
Information Retrieval Basics
Introduction to Recommender Systems
A Common Solution to a Common Problem
Q and A

5. What is Information Retrieval?
Information retrieval is finding material (usually documents) of
an unstructured nature (usually text) that satisfies an information
need from within large collections (usually stored on computers).
Manning
Figure : Information retrieval amongst related scientific areas

6. Documents Indexing
gather documents(sometimes even crawl for them)
preprocess them
use the result to build an effective index

7. Search Engine - General Architecture
Some key terms:
Humans have information needs
... which they convey as querys towards a search engine
... against an index over a documents’ corpus
The result is documents sorted by their relevance for the
query
Usually the query is preprocessed the same way as the indexed
documents.

8. Preprocessing
Let’s observe three documents from a music fans’ forum.
d1 = Rock music rocks my life!
d2 = He loves jazz music.
d3 = I love rock music!

9. Preprocessing
After some language NLP-processing, we get:
d1 = Rock music rocks my life! → { life, music, rock ×2 }
d2 = He loves jazz music. → { jazz, love, music }
d3 = I love rock music! → { love, music, rock }

10. Preprocessing
After some language NLP-processing, we get:
d1 = Rock music rocks my life! → { life, music, rock ×2 }
d2 = He loves jazz music. → { jazz, love, music }
d3 = I love rock music! → { love, music, rock }
Here we have most probably applied language-dependent:
tokenizer
stopwords
lemmatizer
etc.

11. The Boolean Retrieval Model
We build a matrix of all M terms in our dictionary against all N
documents.
For each term/document pair we keep a boolean value that
represents if the document contains the term or not.
d1 = Rock music rocks my life! → { life, music, rock ×2 }
d2 = He loves jazz music. → { jazz, love, music }
d3 = I love rock music! → { love, music, rock }
Table : Corpus of four documents and their boolean index
terms docs d1 d2 d3
jazz 0 1 0
life 1 0 0
love 0 1 1
music 1 1 1
rock 1 0 1

12. The Boolean Retrieval Model
A query, q=“love”
d1 = Rock music rocks my life!
d2 = He loves jazz music.
d3 = I love rock music!
Table : Corpus of three documents and its inverted index
terms docs d1 d2 d3 q
jazz 0 1 0 0
life 1 0 0 0
love 0 1 1 1
music 1 1 1 0
rock 1 0 0 0
Advantages: high recall, fast
Problem: retrieved documents are not rakned

13. The Inverted Index and the Vector-Space Model
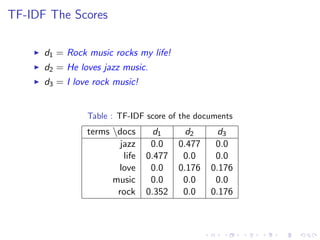
Term-document matrix C[MxN]for M terms and N documents.
Table : We need weights for each term-document couple
terms docs d1 d2 ... dN
t1 w1,1 w1,2 ... w1,N
t2 w2,1 w2,2 ... w2,N
... ... ... ... ...
tM wM,1 wM,2 ... wM,N

14. TF-IDF
We need a metric for how specific each term for each document is.
Term frequency - inverted document frequency very well
serves the purpose.
TF − IDFt,doc = TFt,doc × IDFt
TF − IDFt,doc = tft,doc × log
N
dft
where
tft,doc - number of occurrences of t in doc
dft - number of documents in the corpus, which contains t
N - total number of documents in the corpus

15. TF-IDF Example: The Scores
d1 = Rock music rocks my life!
d2 = He loves jazz music.
d3 = I love rock music!
Table : Corpus of three documents and its inverted index
terms d1 d2 d3
jazz TF − IDF(jazz,d1) TF − IDF(jazz,d2) TF − IDF(jazz,d3)
life TF − IDF(life,d1) TF − IDF(life,d2) TF − IDF(life,d3)
love TF − IDF(love,d1) TF − IDF(love,d2) TF − IDF(love,d3)
music TF − IDF(music,d1) TF − IDF(music,d2) TF − IDF(music,d3)
rock TF − IDF(rock,d1) TF − IDF(rock,d2) TF − IDF(rock,d3)

16. TF-IDF The Scores
d1 = Rock music rocks my life!
d2 = He loves jazz music.
d3 = I love rock music!
Table : TF-IDF score of the documents
terms docs d1 d2 d3
jazz 0.0 0.477 0.0
life 0.477 0.0 0.0
love 0.0 0.176 0.176
music 0.0 0.0 0.0
rock 0.352 0.0 0.176

17. TF-IDF Example
d1 = Rock music rocks my life!
d2 = He loves jazz music.
d3 = I love rock music!
Table : TF-IDF score of the documents. Keywords
terms docs d1 d2 d3
jazz 0.0 0.477 0.0
life 0.477 0.0 0.0
love 0.0 0.176 0.176
music 0.0 0.0 0.0
rock 0.352 0.0 0.176
So we found some key words! Not key phrases, though.

18. TF-IDF Example. Too common to make the difference
d1 = Rock music rocks my life!
d2 = He loves jazz music.
d3 = I love rock music!
The word “music” turns out to be disqualified by TF-IDF, since it
is met in every document from the corpus, and the fact that it
appears in a document from the set, brings no value.
terms docs d1 d2 d3
jazz 0.0 0.477 0.0
life 0.477 0.0 0.0
love 0.0 0.176 0.176
music 0.0 0.0 0.0
rock 0.352 0.0 0.176

19. Executing queries
Table : TF-IDF score of the documents
A query, q=“rock”
terms docs d1 d2 d3
jazz 0.0 0.477 0.0
life 0.477 0.0 0.0
love 0.0 0.176 0.176
music 0.0 0.0 0.0
rock 0.352 0.0 0.176
We know d1 is more relevant than d3 to the “rock” query, and, as
in this corpus, d2 is not relevant at all.

20. Distance between documents
Let’s for a moment ignore the rest of the dimensions(“life” and
“music”) .
Cosine similarity
sim(−→v (di), −→v (dj)) = cos(−→v (di), −→v (dj)) =
−→v (di) · −→v (dj)
|−→v (di)||−→v (dj)|

21. Similarity between documents
Table : TF-IDF score of the documents
terms docs d1 d2 d3
jazz 0.0 0.477 0.0
life 0.477 0.0 0.0
love 0.0 0.176 0.176
music 0.0 0.0 0.0
rock 0.352 0.0 0.176
Table : Cosine similarities between our documents
d1 d2 d3
d1 1.0 0.0 0.593
d2 0.0 1.0 0.245
d3 0.593 0.245 1.0

22. Aspects of the vector space model
Documents are presented as vectors in an M-dimensional space.
Other benefits:
comfortable for query search
comfortable for text classification
comfortable for document clustering
Negative sides:
might be subject to sparsity
polysemy
synonymy
... so we might need a glance at semantics

23. Although finding synonyms...
Can be achieved in a big enough model(with big enough corpora)
by looking into the cooccurrence of the term and hence their
probable relation.
M = CCT
Table : Terms correlation
jazz life love music rock
jazz 0.228 0.0 0.084 0.0 0.0
life 0.0 0.228 0.0 0.0 0.168
love 0.084 0.0 0.062 0.0 0.031
music 0.0 0.0 0.0 0.0 0.0
rock 0.0 0.168 0.031 0.0 0.155

24. Related Software
Apache Lucene
Apache Solr
ElasticSearch
Apache Nutch

25. What are Recommender Systems?
Software systems that suggests to users items of interest by
anticipating their rating/likeness/relevance to the items. The latter
might be for example:
friends to follow
products to buy
music videos to watch online
new books to read
etc, etc, etc
Let’s see some examples.

26. Amazon: recommendation of similar books to read

27. YouTube: personalized videos recommendation

28. IMDB: related movies to watch

29. Types of recommender systems
Recommender system approaches
Collaborative filtering
Content-based approach
Hybrid approaches

30. Collaborative filtering
This is recommendation approach in which only the users’
activity is taken into account.
People are being recommended items on the basis of what
similar users liked/rated highly/purchased.
Because users with similar ratings have most probably similar
taste and will rate items in a common fashion.
Table : Exemplary rating of 4 users for 5 random movies on a 1 to 5 scale
LA NH BJD FF O11
Anna 5 4 5 2 ?
Boyan 5 4 1
Ciana 2 1 4
Deyan 1 2 5

31. Centered user ratings
Subtract from each user’s ratings the average of his/her rating.
Table : Initial ratings
LA NH BJD FF O11
Anna 5 4 5 2
Boyan 5 4 1
Ciana 2 1 4
Deyan 1 2 5
Table : Centered ratings. The sum at each row is 0.
LA NH BJD FF O11
Anna 1 0 1 -2 0
Boyan 0 5
3
2
3 0 -7
3
Ciana −1
3 0 −4
3 0 5
3
Deyan 0 −5
3 −2
3 0 7
3

32. Centered cosine similarity/Pearson Correlation
Applied to find similar users for user-to-user collaborative filtering.
Table : Initial ratings
LA NH BJD FF O11
Anna 1 0 1 -2 0
Boyan 0 5
3
2
3 0 -7
3
Ciana −1
3 0 −4
3 0 5
3
Deyan 0 −5
3 −2
3 0 7
3
sim(−→v (“Anna ), −→v (“Boyan ) = cos(−→v (“Anna ), −→v (“Boyan ) = 0.092
sim(−→v (“Anna ), −→v (“Ciana ) = cos(−→v (“Anna ), −→v (“Ciana ) = −0.315
sim(−→v (“Anna ), −→v (“Deyan ) = cos(−→v (“Anna ), −→v (“Deyan ) = −0.092
sim(−→v (“Boyan ), −→v (“Deyan ) = cos(−→v (“Boyan ), −→v (“Deyan ) = −1.0

33. Collaborative filtering. User-to-User Approach
Take the most similar users to user X and predict X’s taste on the base of their
ratings. The rating of user i for movie j, where SU(i) are user i’s most closest user is
then given by:
rij =
m∈SU(i) sim(m, j) ∗ rmj
m∈SU(i) sim(m, j)
Example:
SU(Anna) = {Boyan}
rBoyan,O11 = −
7
3
Our prediction for
rAnna,O11 =
0.092 ∗ (−7
3
)
0.092
= −
7
3
RAnna,O11 = avg(RAnna,j ) + rAnna,O11 = 4 −
7
3
= 1.67
For each user we need to first screen out the best similar users, then rate each
element separately
Then we suggest the items with highest predicted ratings to the user

34. Collaborative filtering. Item-to-Item Approach
Instead of similar users to users, we find similar items to items,
based on the ratings. SI(i) stands for the similar items to item i.
rij =
m∈SU(j) sim(m, j) ∗ rim
m∈SU(i) sim(m, j)
SI(LA) = BJD, sim(LA, BJD) = 0.715
rBoyan,LA =
0.715 ∗ 0.667
0.715
= 0.667
RBoyan,LA = avg(i, LA) + rBoyan,LA = 3.5 + 0.667 = 4.167
Item-to-item collaborative filtering turns out to be more
effective than user-to-user, since items have more constant
behaviour that humans :)

35. Collaborative filtering. Results
Table : Our new results
LA NH BJD FF O11
Anna 5 4 5 2 1.67
Boyan 4.167 5 4 1
Ciana 2 1 4
Deyan 1 2 5

36. The “Cold start” problem
New user. We have no information about a new user, hence
we cannot find similar users and recommend based on their
activity
workaround: offer the newest or highest ranking items ro this
user
New item. We have no information about new item and hence
cannot relate it to other(rated) item
workaround: the newest items for at least several times are
recommended to the most active users

37. Content-based approach
Items’ content is observed. No cold start for new item :) Still
have the cold start on new user, though.
Users are generated a profile on the basis of the content
of the items they liked
This profile can be represented by a vector of weights in the
content representation space
Then, the user’s profile can be examined for proximity to
items in this space
Back to the vector-space model and the documents space...
The user profile can be viewed as a dynamic document!

38. Forming a User Profile
Imagine a lyrics forum, into which users are recommended
lyrics based on previously liked lyrics
Each user has liked certain lyrics
We need to recommend other lyrics a user might like, based
on similarity of content
For each piece of lyrics that the user liked, their ”profile“ is
updated, e.. like this:
−→v (user) = Σd∈Duserliked
−→
d
scoreuser,term = Σd∈Duserliked
wt,d

39. Users become documents!
Table : TF-IDF score of the documents/user profiles
terms docs d1 d2 d3 ... Anna Boyan
... ... ... ... ... ... ...
jazz 0.0 0.477 0.0 ... 0.073 0.0
life 0.477 0.0 0.0 ... 0.211 0.023
love 0.0 0.176 0.176 ... 0.812 0.345
music 0.0 0.0 0.0 ... 0.0 0.0
rock 0.352 0.0 0.176 ... 0.001 0.654
... ... ... ... ... ... ...
We can add document classes, extracted topics, extracted named
entities, locations, etc. to the model. Also, e.g. actors or directors
for IMDB, musicians or vlogger for YouTube, and so forth.
Anything that is related to the user and is found in the
documents(or their metadata).

40. Some time-related insights
Use time decay factor
some user interests or inclinations are temporary
e.g. ”curling“ during the Winter Olympics or ”wedding“
around a person’s wedding
so it is nice idea to periodically decrease the score of a user’s
topics, so that the old-favourite topics decline
hint: don’t actualize data for non-active users
Use only active users
it might be good idea to (temporarily) reduce the data size by
ignoring ancient users

41. The problem with dimensionality and sparsity
Imagine...
N = 10,000,000 users
200, 000 items
in a vector-space of M = 1,000,000 terms
how do we use our sparse matrix C[NxM]?

42. The problem with dimensionality and sparsity
Imagine...
N = 10,000,000 users
200, 000 items
in a vector-space of M = 1,000,000 terms
how do we use our sparse matrix C[NxM]?
OMG!!! This is big data!!!
;)

43. Latent Semantic Indexing
a.k.a Latent Semantic Analysis to te rescue.
We use SVD as a low-rank approximation of the orginal space. We
reduce both memory needed and noise. Also, we find semantic
notions in the data.

44. Singular Value Decomposition
Theorem. (Manning) Let r be the rank of the M x M matrix C.
Then, there is a singular value decomposition(SVD) of C of the
form:
C = UΣV T
where
The eigenvalues λ1, ..., λr of CCT are the same as the
eigenvalues of CT C
For 1 ≤ i ≤ r, letσi =
√
λi , with λi ≥ λi+1. Then the M x N
matrix Σ is composed by setting Σii = σi for 1 ≤ i ≤ r, and
zero otherwise.
σi are called singular values of C
the columns of U - left-singular vectors of C
the columns of V - right-singular vectors of C

45. Singular Value Decomposition in Picures

46. Singular Value Decomposition in R
SVD is commonly computed by the Lanczos algorithm. Or simply
in R :)

47. LSI in Picures
Used for low-rank approximation.

48. LSI in Recommedations
Σ =




4.519 0 0 0
0 2.477 0 0
0 0 1.199 0
0 0 0 0.000




Table : Centered ratings. Higher ratings are in red.
LA NH BJD FF O11
Anna 1 0 1 -2 0
Boyan 0 5
3
2
3 0 -7
3
Ciana −1
3 0 −4
3 0 5
3
Deyan 0 −5
3 −2
3 0 7
3
The first three movies can be regarded as ”romantic“, the second
two - ”action“.

49. LSI in IR
the query is adapted to use the low-rank approximation
noise is cleared and the model is improved
synonyms and better handles
other values are still subject of investigation

50. Discussion time!
QUESTIONS!

51. Thanks
Thank You for Your Time!
Now it’s beer time! :)