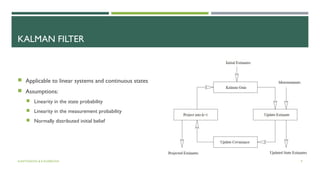
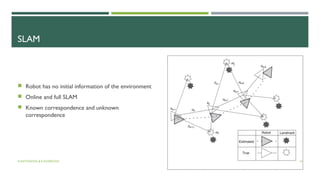
The document discusses various AI methods for localization in noisy environments, including position tracking, mapping, and techniques for robot localization like Bayesian filters and Kalman filters. It covers specific algorithms such as Extended Kalman Filter and Particle Filter, addressing their applications, assumptions, and computational efficiencies. Additionally, it touches on Simultaneous Localization and Mapping (SLAM) techniques, including EKF SLAM and FastSLAM, alongside their requirements and advantages.

1. AI METHODS FOR LOCALIZATION IN NOISY
ENVIRONMENT
ANA ANTONOVA & KAMELIA KOSEKOVA

2. GITHUB REPOS
 dataepisteme/AI-for-Localization
 datasciencesociety/Lego-Mindstorm
A.ANTONOVA & K.KOSEKOVA 2

3. LOCALIZATION?
 Position Tracking Global
Localization Kidnapped Robot
 Static and Dynamic Environment
 Passive and Active Localization
 Localization and Mapping
A.ANTONOVA & K.KOSEKOVA 3

4. UNCERTAINTY
 Environments
 Sensors
 Robots
 Models
 Computation
A.ANTONOVA & K.KOSEKOVA 4

5. TECHNIQUES FOR ROBOT LOCALIZATION
A.ANTONOVA & K.KOSEKOVA
5

6. SOME IMPORTANT NOTIONS
 State
x0:t = {x0,x1, x2…,xt }
 Observation/measurement
z1:t = {z1,z2, z3…,zt }
 Control data
u1:t = {u1,u2, u3…,ut }
A.ANTONOVA & K.KOSEKOVA 6

7. BAYES FILTER
 Bayes theorem  Markov chain process
A.ANTONOVA & K.KOSEKOVA 7

8. GAUSSIAN FILTERS
 Earliest implementations of the Bayes filter
 Assumptions:
 Beliefs are represented by multivariate normal distributions
 Properties of Gaussians:
 Unimodal
A.ANTONOVA & K.KOSEKOVA 8

9. KALMAN FILTER
 Applicable to linear systems and continuous states
 Assumptions:
 Linearity in the state probability
 Linearity in the measurement probability
 Normally distributed initial belief
A.ANTONOVA & K.KOSEKOVA 9

10. EXTENDED KALMAN FILTER
 Applicable to nonlinear systems
 Applies linearization via Taylor expansion
 Approximates the nonlinear functions -> leads to a
Gaussian posterior belief
 The most popular tool for state estimation
 Computationally efficient
 Drawbacks: Uncapable of representing multi-modal
beliefs
A.ANTONOVA & K.KOSEKOVA 10GitHub: AtsushiSakai/PythonRobotics

11. EKF LOCALIZATION
 Special case of Markov localization
 Well-suited technique for local position tracking with limited uncertainty and in environments with distinct
features (landmarks)
 Initial position is known
 For the implementation of the algorithm we need the following:
 Motion model
 Measurement model
 Map of the environment
A.ANTONOVA & K.KOSEKOVA 11

12. PARTICLE FILTER
 Approximates the posterior by a finite number of
parameters
 A random state samples (particles) drawn from the
posterior
 Each particle is a hypothesis to the true state
 Uses importance resampling to form a set of particles
 This set of particles approximates the belief
A.ANTONOVA & K.KOSEKOVA 12
Jeremy Cohen, “Self-Driving Cars & Localization”

13. MONTE CARLO LOCALIZATION
 Uses particle filter
 Able to solve local/global localization and kidnapped robot problems (recover from localization failure)
 The kidnapped robot problem is solved by adding random particles
 Able to process raw sensor measurements and negative information
 The accuracy-computational costs trade-off is achieved through the size of the particle set
 For the implementation of the algorithm we need the following:
 Motion model
 Measurement model
 Map of the environment
 Initial belief
A.ANTONOVA & K.KOSEKOVA 13

14. SLAM
 Robot has no initial information of the environment
 Online and full SLAM
 Known correspondence and unknown
correspondence
A.ANTONOVA & K.KOSEKOVA 14

15. EKF SLAM
Underwater vehicle Oberon, developed at the University of Sydney. Image
courtesy of Stefan Williams and Hugh Durrant-Whyte.
 Earliest application of SLAM
 Some assumptions:
 Feature-based maps
 Gaussian noise
 Positive measurements
 Online SLAM
A.ANTONOVA & K.KOSEKOVA 15

16. FASTSLAM
 Resolving the computational complexity of EKF SLAM
 Each Particle in the algorithm get separate landmark
estimators for each landmark – log(N) time.
A.ANTONOVA & K.KOSEKOVA 16
GitHub: AtsushiSakai/PythonRobotics

17. 17
“FastSLAM: A Factored Solution to theSimultaneous Localization and Mapping
ProblemWith Unknown Data Association”, M. Montemerlo

18. THANKYOU!
A.ANTONOVA & K.KOSEKOVA 18
Q&A