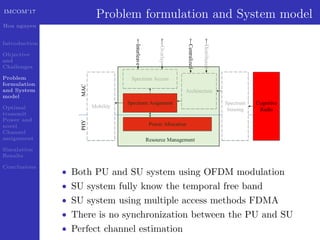
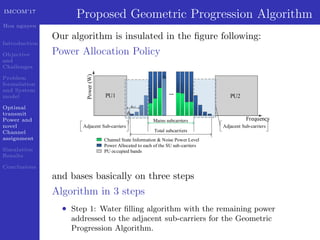
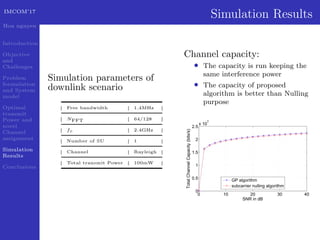
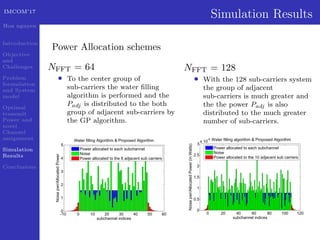
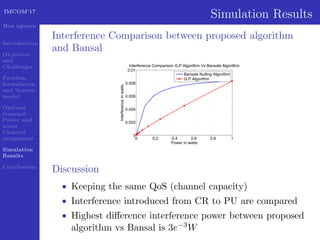
This document presents a geometric progression algorithm for adjacent band power allocation in OFDM-based cognitive radio. The objectives are to minimize interference from secondary users to primary users through optimal transmit power allocation and a novel channel assignment method. The proposed algorithm allocates power to center subcarriers using waterfilling and distributes remaining power to adjacent subcarriers geometrically. Simulation results show the algorithm achieves higher capacity than subcarrier nulling and introduces less interference to primary users compared to an existing method. In conclusion, an analytic closed-form solution is derived for optimal power allocation and the geometric progression algorithm is presented and verified through simulations.

1. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Geometric Progression Algorithm for
Adjacent Band Power Allocation in OFDM
based Cognitive Radio
Tien Hoa Nguyen; H´elio Augusto; Van Duc nguyen
Email: hoa.nguyentien@hust.edu.vn
Hanoi University of Science and Technology
January 4, 2017

2. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Outline
1 Introduction
2 Objective and Challenges
3 Problem formulation and System model
4 Optimal transmit Power and novel Channel assignment
5 Simulation Results
6 Conclusions

3. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Introduction
• Cognitive radios (CR) can support new wireless users in
existing crowded spectrum without degrading
performance of primary users (PU)
• Utilize advanced communication and signal processing
techniques, coupled with novel spectrum allocation
policies
• Technology could revolutionize the way spectrum is
allocated worldwide and provide sufficient bandwidth to
support higher quality and higher data rate products
and services

4. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Cognitive Radio Paradigms
• Underlay:
• CR constrained to cause limited interference to PU
• The interference constraint may be met via wideband
signalling to maintain interference below the noise floor
• Interweave:
• Cognitive radios find and exploit spectral holes to avoid
interfering with noncognitive radios.
• Transmit if interference below a given threshold

5. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Objective and Challenges
Objective
Minimize the interference from SU to PU by:
• providing analytic optimal transmit power allocation in
closed-form for CR-OFDM system with channel
throughput constraints
• proposing a novel Geometric Progression Algorithm for
Adjacent Band Power Allocation in OFDM based
Cognitive Radio
Challenges
Different from all the aforementioned studies, this paper
considers a wireless peer-to-peer Cognitive Radio Network,
where multiple cognitive links coexist with multiple primary
links, therefore inter-users (IUI) and mutual-users (MUI)
interference have to be considered.

6. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Problem formulation and System model
Cognitive
Radio
Architecture
Spectrum Access
Power Allocation
Spectrum
Sensing
Mobility
MACPHY
Spectrum Asignment
Overlay
Centralized
Distributed
Interleave
Resource Management
• Both PU and SU system using OFDM modulation
• SU system fully know the temporal free band
• SU system using multiple access methods FDMA
• There is no synchronization between the PU and SU
• Perfect channel estimation

7. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Problem formulation and System model
Coexisting model
• K Tranceiver pairs SU using
OFDM
• L active PU bands
• 3 channels: hss
i,j; hsp
i,l; hps
l,i
Cost function
I = minPn
L
l=1
N
n=1 |h
(sp)
n |2
Pn
d
(l)
n + B(l)
2
d
(l)
n − B(l)
2
sin(πfTs)
πfTs
2
df
Constraints
C = N
n=1 Bn ln 1 + |h
(ss)
n |2
Pn
σ2+ L
l=1
J
(l)
n
≥ Cth
Pi = 0

8. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Closed-form of optimal transmit power
Using Lagrange function with KKT constraints
L(. . . ) =
L
l=1
N
n=1
|h
(sp)
n |2
Pn
d
(l)
n + B(l)
2
d
(l)
n − B(l)
2
sin(πfTs)
πfTs
2
df+
+ λ
N
n=1
Bn ln 1 +
|h
(ss)
n |2Pn
σ2 + L
l=1 J
(l)
n
− Cth +
N
n=1
µnPn = 0
s.t.
N
n=1
Bn ln 1 +
|h
(ss)
n |2Pn
σ2 + L
l=1 J
(l)
n
− Cth = 0
Pi = 0
Let denote K
(l)
n = ∂I
(l)
n
∂Pn
and Ψ
(l)
n =
|h
(ss)
n |2
σ2+ L
l=1
J
(l)
n
the optimal
transmit power in closed-form is given as:
Pn = max{0,
λBn
N
n=1 K
(l)
n
−
1
Ψ
(l)
n
}

9. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Proposed Geometric Progression Algorithm
Our algorithm is insulated in the figure following:
Power Allocation Policy
PU1 PU2
Frequency
Power(W)
Total subcarriers
...
Mains subcarriers
dn
dn-2
Channel State Information & Noise Power Level
Power Allocated to each of the SU sub-carriers
PU occupied bands
Adjacent Sub-carriersAdjacent Sub-carriers
and bases basically on three steps
Algorithm in 3 steps
• Step 1: Water filling algorithm with the remaining power
addressed to the adjacent sub-carriers for the Geometric
Progression Algorithm.

10. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Proposed Geometric Progression Algorithm
Algorithm in 3 steps (continues)
• Step 2: Choosing for the adjacent sides n sub-carriers, or 2nd
sub-carriers for the both adjacent sides. Here q is the ratio of the
distribution. The total adjacent power Padj is distributed so that
Padj = n
i=1 Pi with n = 0. The interference caused by Padj must
be less than the interference caused by Pwth which is the power
that can cause the maximum and allowed interference Ith
• Step 3: The power Padj is assigned by following the algorithm:
Pn = Padj × 2n−1
with n = 0, where Pn is the power to be
allocated to each of the sub-carriers.

11. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Simulation Results
Simulation parameters of
downlink scenario
Free bandwidth 1.4MHz
NFFT 64/128
fc 2.4GHz
Number of SU 1
Channel Rayleigh
Total transmit Power 100mW
Channel capacity:
• The capacity is run keeping the
same interference power
• The capacity of proposed
algorithm is better than Nulling
purpose
0 10 20 30 40
0
0.5
1
1.5
2
2.5
x 10
7
TotalChannelCapacity(bits/s)
SNR in dB
GP algorithm
subcarrier nulling algorithm

12. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Simulation Results
Power Allocation schemes
NFFT = 64
• To the center group of
sub-carriers the water filling
algorithm is performed and the
Padj is distributed to the both
group of adjacent sub-carriers by
the GP algorithm.
-10 0 10 20 30 40 50 60
0
1
2
3
4
5
subchannel indices
Noisepwr/AllocatedPower
Water filling Algorithm & Proposed Algorithm
Power allocated to each subchannel
Noise
Power allocated to the 8 adjacent sub carriers
NFFT = 128
• With the 128 sub-carriers system
the group of adjacent
sub-carriers is much greater and
the the power Padj is also
distributed to the much greater
number of sub-carriers.
0 20 40 60 80 100 120
0
0.5
1
1.5
2
2.5
3
x 10
-5
subchannel indices
Noisepwr/AllocatedPower(inWatts)
Water filling algorithm & Proposed Algorithm
Power allocated to each subchannel
Noise
Power allocated to the 10 adjacent sub carriers

13. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Simulation Results
Interference Comparison between proposed algorithm
and Bansal
0 0.2 0.4 0.6 0.8 1
0
0.002
0.004
0.006
0.008
0.01
Power in watts
Interferenceinwatts
Interference Comparison G.P Algorithm Vs Bansals Algorithm
Bansals Nulling Algorithm
G.P Algorithm
Discussion
• Keeping the same QoS (channel capacity)
• Interference introduced from CR to PU are compared
• Highest difference interference power between proposed
algorithm vs Bansal is 3e−3W

14. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Conclusions
1 Provides analytic optimal transmit power allocation in
closed-form for CR-OFDM multi-user system in
network model
2 Proposed a Geometric Progression Algorithm
3 It was compared the interference caused by the SU to
the PU of proposed algorithm with Scheme A of
Bansal’s

15. IMCOM’17
Hoa nguyen
Introduction
Objective
and
Challenges
Problem
formulation
and System
model
Optimal
transmit
Power and
novel
Channel
assignment
Simulation
Results
Conclusions
Thank you for your attention
and
I am looking forward to hear your questions