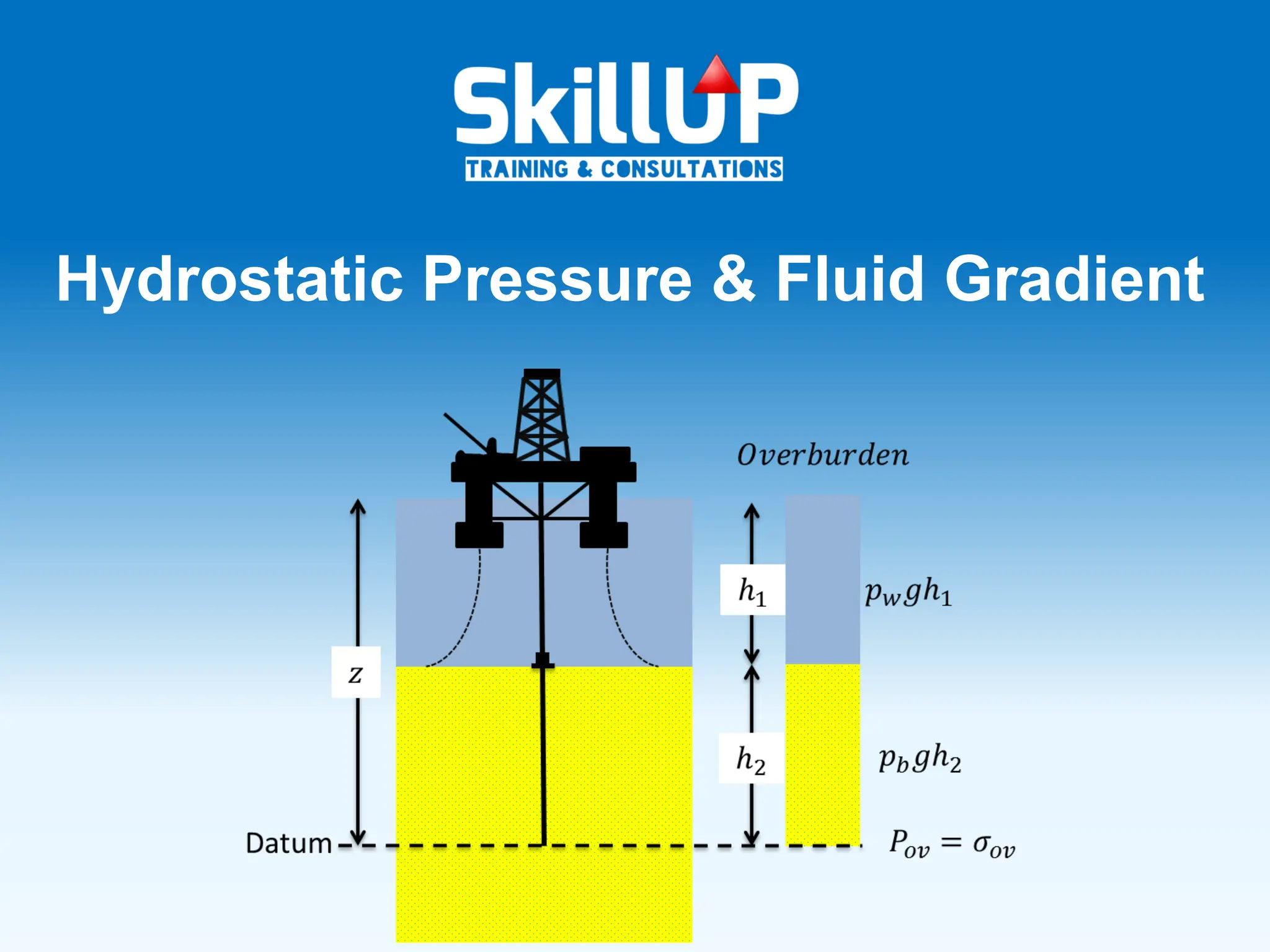
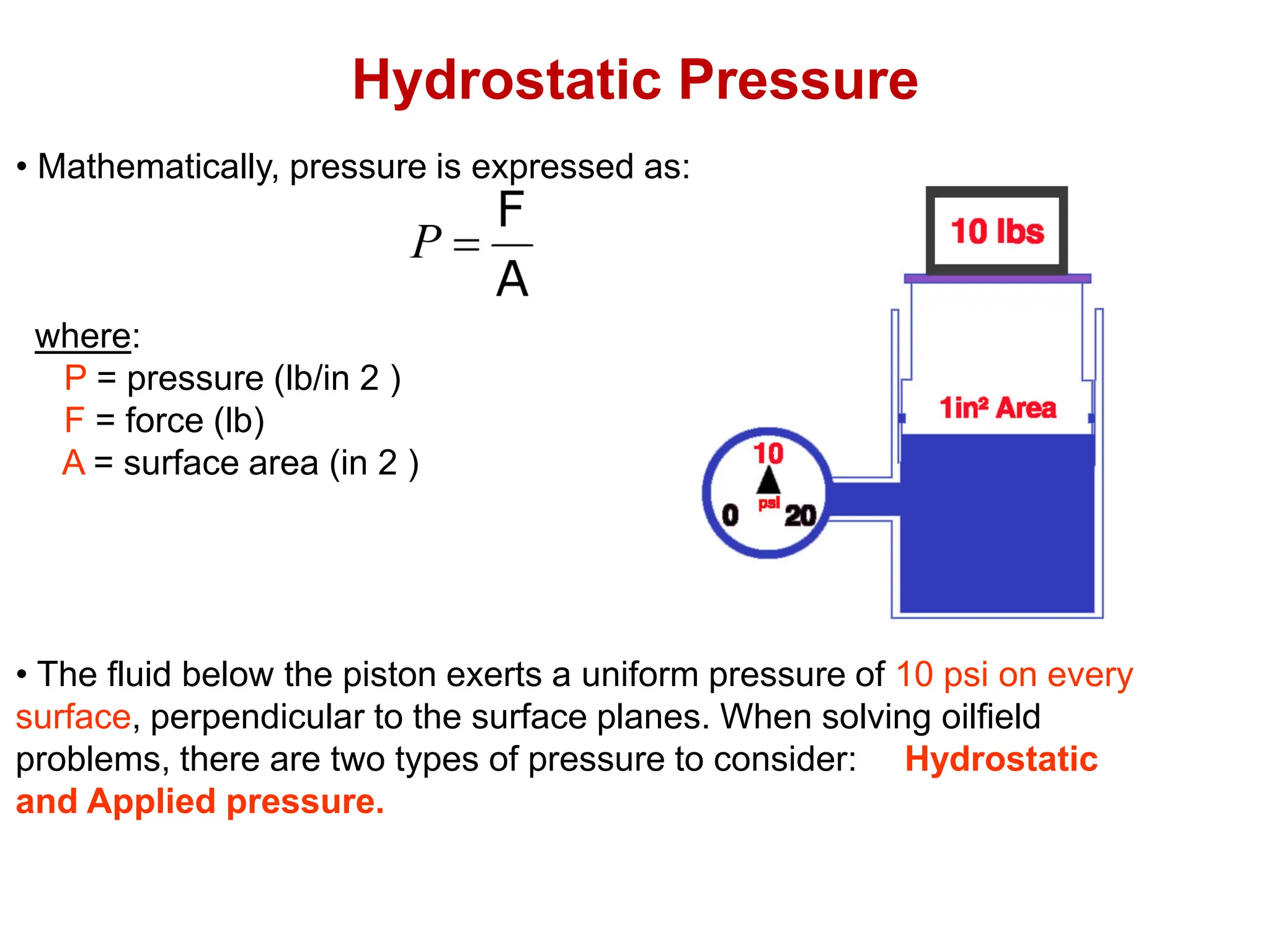
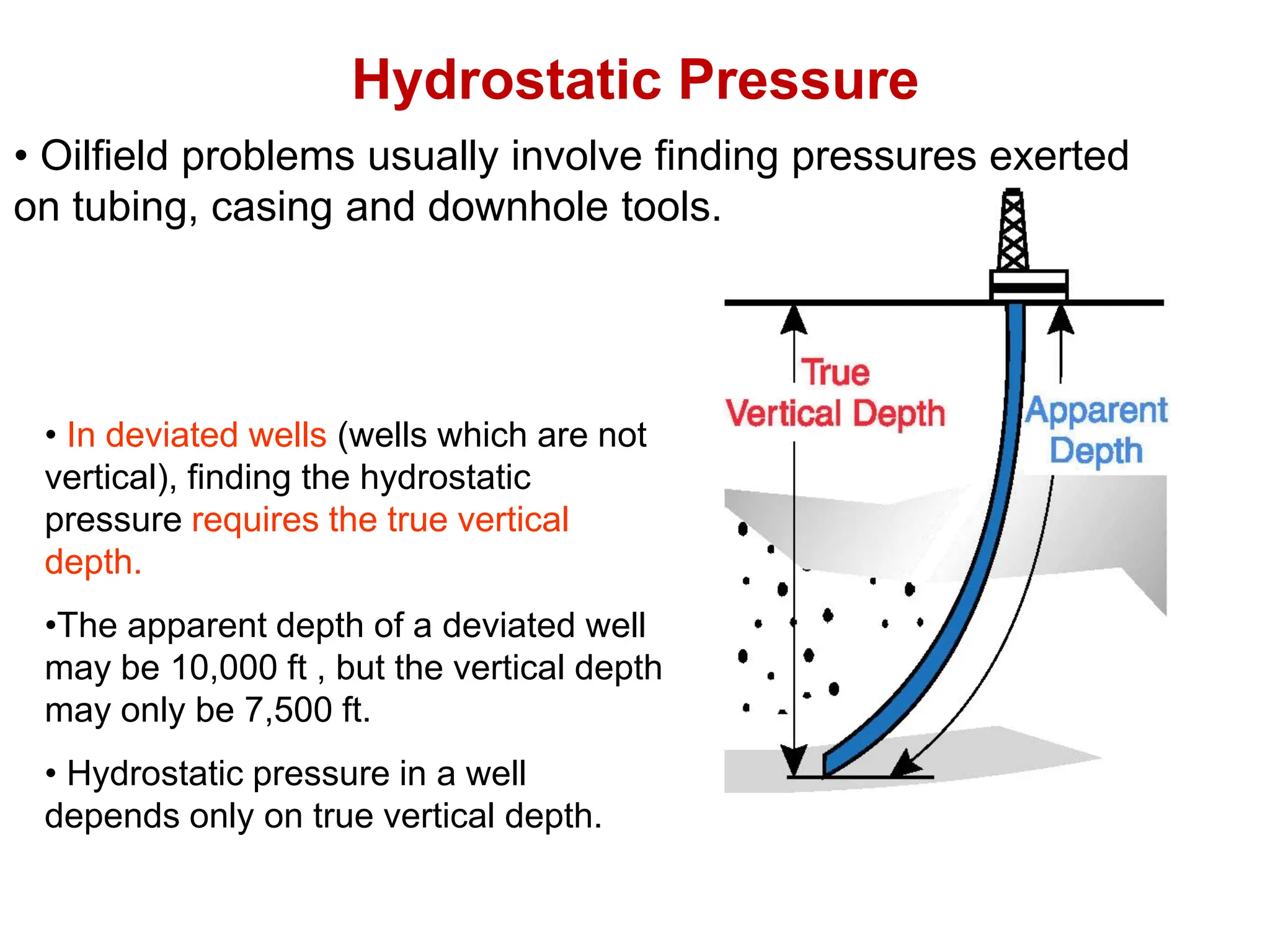
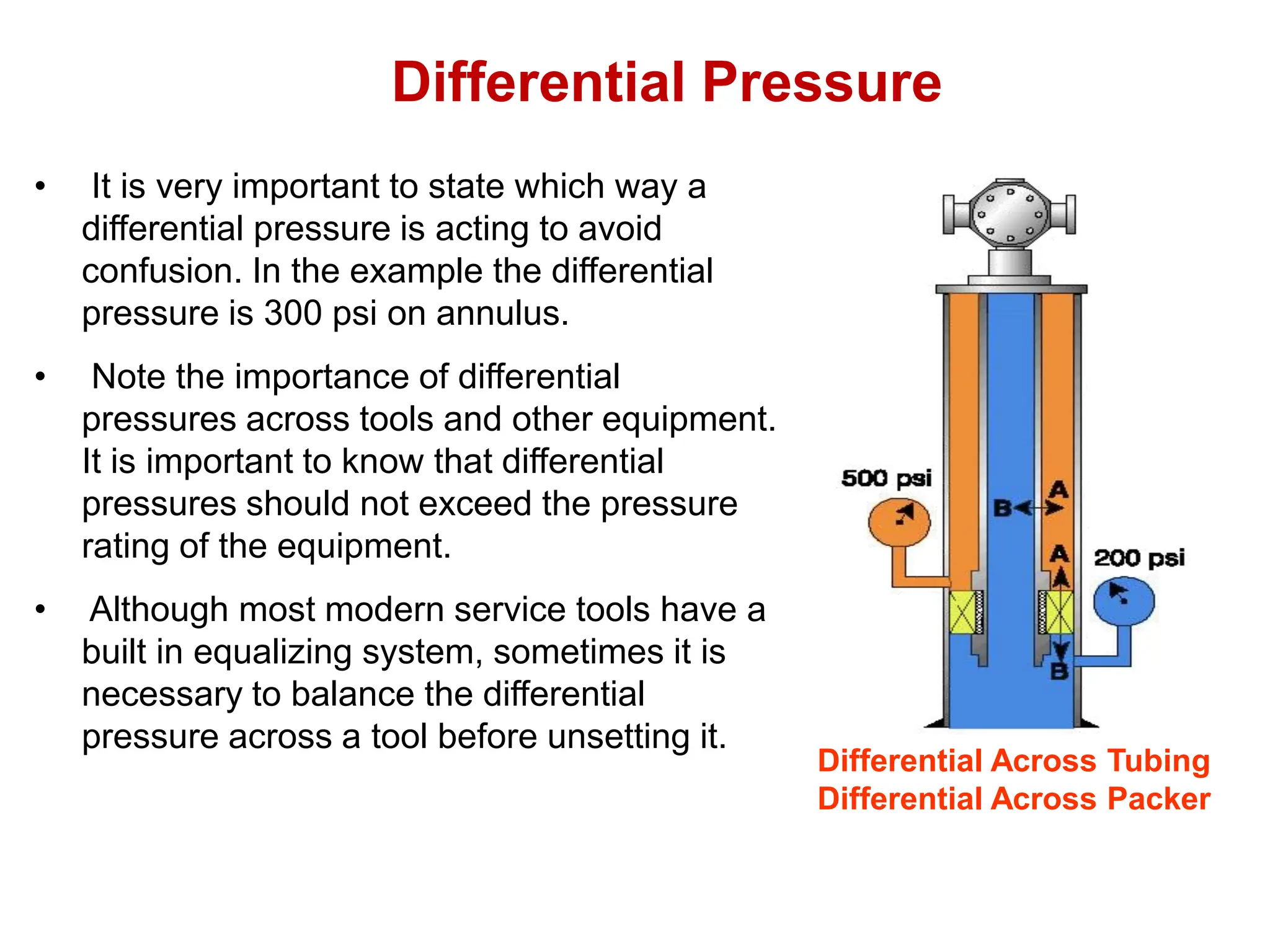
Hydrostatic pressure is the pressure exerted by a fluid due to the weight of the fluid above it. It depends on the density of the fluid and the depth below the surface. To calculate hydrostatic pressure, use the formula: P = W x H, where P is pressure, W is fluid weight, and H is true vertical depth. True vertical depth, not measured depth, must be used because hydrostatic pressure only depends on the direct vertical distance through the fluid column. Fluid gradients are used instead of fluid weights to simplify hydrostatic pressure calculations.

1. Hydrostatic Pressure & Fluid Gradient

2. • Pressure is defined as the force exerted by a fluid that is in some way
confined in a vessel, pipe, or hole in the ground, such as that exerted on
the bottom of the wellbore by drilling mud. It is expressed in terms of
force per unit area (pounds per square inch).
• EX : A force of 10 pounds ( #)
pushing on a surface with 1
square inch ( in2) of area
would exert a pressure of 10
pounds per square inch (psi)
on that surface.
Hydrostatic Pressure

3. • Mathematically, pressure is expressed as:
where:
P = pressure (lb/in 2 )
F = force (lb)
A = surface area (in 2 )
• The fluid below the piston exerts a uniform pressure of 10 psi on every
surface, perpendicular to the surface planes. When solving oilfield
problems, there are two types of pressure to consider: Hydrostatic
and Applied pressure.
Hydrostatic Pressure

4. Hydrostatic Pressure
• Hydrostatic pressure is fluid pressure due to the weight of
fluid above it. Both gases and liquids exert hydrostatic
pressure.
• Hydrostatic pressure is present at all points below the
surface of a fluid, but unlike applied pressure it is not
constant. The hydrostatic pressure at any point depends on
the fluid density and the depth below the fluid surface.
• A good example of hydrostatic pressure is atmospheric
pressure. The weight of the air causes an average pressure
of 14.7 psi at sea level. It is well known that as elevation
above sea level increases, air pressure decreases.

5. • Oilfield problems usually involve finding pressures exerted
on tubing, casing and downhole tools.
• In deviated wells (wells which are not
vertical), finding the hydrostatic
pressure requires the true vertical
depth.
•The apparent depth of a deviated well
may be 10,000 ft , but the vertical depth
may only be 7,500 ft.
• Hydrostatic pressure in a well
depends only on true vertical depth.
Hydrostatic Pressure

6. Calculating Hydrostatic Pressure
• The term hydrostatic is used to describe the pressure of a fluid. It
comes from the words hydro, which means water or liquid, and static,
which means at rest.
• The weight of a column of fluid exerts a hydrostatic pressure, and the
pressure is dependent upon two things:
· Density of the fluid
· Height of the fluid column
• The units for fluid weight are lb/gal, lb/ft 3 or lb/in 3 . To determine
hydrostatic pressure, the following formula may be used:
P = W × H
Where: P = hydrostatic pressure
W = fluid weight
H = true vertical depth

7. Calculating Hydrostatic Pressure
• The pressure does not depend at all on the diameter of the well,
but only the height and density of the column of fluid. If a plot of hydrostatic
pressure vs. depth is made we can see that hydrostatic pressure at the top
of the well is zero and increases linearly with depth.
• When the density of the fluid is measured in pounds per gallon (lb/gal), the
density can be converted to a pressure gradient in psi per foot as shown
below.
The formula then becomes:
• Hydrostatic pressure (psi) = fluid wt (lb/gal) x 0.05195 x depth (ft)

8. Calculating Hydrostatic Pressure
• When the density of the fluid is measured in pounds per cubic foot
(lb/ft3),the density can be converted to a pressure gradient in psi per foot
as shown below.
The formula then becomes:
Hydrostatic pressure = fluid wt (lb/ ft3) x depth ft ÷ 144
• When the density of the fluid is measured in API gravity,the density can
be converted to a pressure gradient in psi per foot as shown below.
The formula then becomes:
Hydrostatic pressure = x depth ft
5
.
131
API
317
.
61



9. True Vertical Depth
• One important thing to understand when calculating hydrostatic pressure
is that hydrostatic is a function of true vertical depth, TVD, not measured
depth, MD ( Apparent depth).
• TVD is determined by finding the
depth in a straight vertical line from the
point of measurement to the surface.
• Measured depth is the length of pipe
or wireline required to reach the point
of measurement, and has nothing to do
with the hydrostatic pressure.

10. True Vertical Depth
• Which of the following three wells will have the highest hydrostatic
pressure at the bottom of the well?
• The hydrostatic pressure at the bottom is the same in all three wells
because the TVD is the same.

11. True Vertical Depth
• The vertical depth of the two wells
are the same, but it would require
more pipe to get to the bottom of
the deviated well, this is called
MEASURED DEPTH (MD)
• If the average angle of the well
opposite is 200 what would be the
TVD
1000 ft
Always use TVD to calculate
hydrostatic
7000 ft

12. Applied Pressure
• Applied pressure is due to a pump or similar means. Applied
pressure is felt throughout the system equally. Example, applying
5,000 psi inside of a pipe exerts 5,000 psi everywhere on the pipe
wall regardless of the pipe size. Applying 5,000 psi at the surface of a
10,000 ft. well will exert 5,000 psi throughout the well bore.
• When pressure is applied at surface the
pressure anywhere in the well is equal to the
hydrostatic pressure at that point plus the
applied pressure.
At the surface: P = (0.433 x 0) + 5000 = 5000 psi
At the bottom: P = (0.433 x 10000) + 5000 = 9330 psi
5000 psi applied
10000 ft
Fresh
water

13. Differential Pressure
• Differential pressure is the pressure
across a tool, tubing wall, etc. If the
pressure in the annulus is 500 psi and
the pressure in the tubing string is 200
psi, there is a pressure differential across
the tool and across the tubing wall.
• The magnitude of the differential
pressure is the difference between the
two pressures, 300 psi.
• Differential pressure equation is:
•
• Pdiff =Pa – Pb
Pdiff =Pa – Pb
Pdiff = differential pressure
Pa = pressure @ point a
Pb = pressure @ point b

14. Differential Pressure
• It is very important to state which way a
differential pressure is acting to avoid
confusion. In the example the differential
pressure is 300 psi on annulus.
• Note the importance of differential
pressures across tools and other equipment.
It is important to know that differential
pressures should not exceed the pressure
rating of the equipment.
• Although most modern service tools have a
built in equalizing system, sometimes it is
necessary to balance the differential
pressure across a tool before unsetting it.
Differential Across Tubing
Differential Across Packer

15. Fluid Gradients
• Since there are a variety of ways to specify the fluid
weight, it is cumbersome to use it when determining
hydrostatic pressure. To avoid changing fluid weight and
depth into similar units, hydrostatic pressure is usually
defined by fluid gradient. Fluid gradient is the pressure
exerted per unit depth of a fluid and is derived by
manipulating the units.
• For example, the fluid weight of 38° API oil is 52.06 lb/ft3.
This can also be expressed as 52.06 lb/ft2/ft or lb/ft2 per ft.
The
units lb/ ft2 are units of pressure and are changed into lb/in
2 by multiplying by the conversion factor .006944 ft 2 /in 2 .
52.06 lb/ft3 × .006944 ft2/in2 =.362 lb/in2/ft =.362 psi/ft

16. Fluid Gradients
• If the fluid weight is in lb/gal, multiplying the fluid weight by
.05195 gal/(ft. in2) will give the fluid gradient. The engineering
tables list fluid gradients in various units to simplify the
calculations.
Multiplying the fluid gradient by the depth will give the
hydrostatic pressure at the specified depth.
P = fg × h
where:
P = hydrostatic pressure (psi)
fg = fluid gradient (psi/ft)
h = true vertical depth (ft)