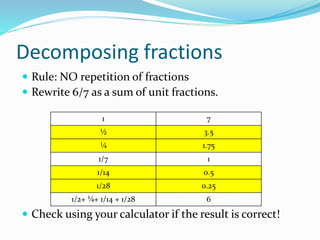
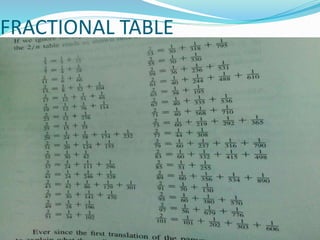
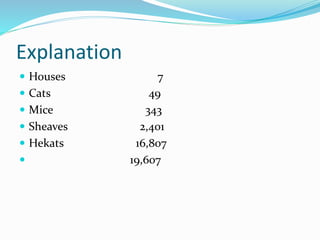
The document discusses Egyptian mathematics as recorded in historical papyri. It describes how the Egyptians developed mathematics out of practical needs like commerce, construction, and taxation of agricultural land. Much of our knowledge comes from the Rhind and Moscow papyri, which contain early examples of arithmetic operations like multiplication and fraction decomposition. The Rosetta Stone later helped decipher Egyptian hieroglyphics. Key figures who advanced the field include Champollion, who established the translation of hieroglyphics, and Rhind and Moscow, after whom the important papyri are named. The document provides several examples of early Egyptian arithmetic techniques.

1. Feljone G. Ragma, Ed.D.

2. Egyptian Mathematical Papyri
 Mathematics arose from practical needs. The
Egyptians required ordinary arithmetic in the daily
transactions of commerce and to construct a workable
calendar.
 Simple geometric rules were applied to determine
boundaries if fields and the contents of granaries.
 According to Herodotus, Egypt if the gift of the Nile
and Geometry is the second gift.
 Due to annual inundation of the Nile valley, it became
necessary for purposes of taxation to determine how
much land had been gained or lost.

3. Egyptian Mathematical Papyri
 The initial emphasis was on utilitarian mathematics.
 Algebra evolved ultimately from the techniques of
calculation, and theoretical geometry began with land
measurement.
 Most of our knowledge of early mathematics in Egypt
comes from two sizable- each named after its former
owner- the RHIND PAPYRUS and the
GOLENISCHEV or the MOSCOW PAPYRUS.

4. The RHIND Papyrus
 It was found in Thebes, in the ruins of a small
building near the Ramessuem.
 It was purchased in Luxor, Egypt in 1858 by Henry
Rhind. Later on, it was willed to the British Museum.
 It was written in hieratic script by Ahmes
 It was a scroll 18 feet long and 13 inches high.

5. The Rosetta Stone
 It is a slab of polished black basalt.
 It was found during the Napoleon’s expedition.
 It was uncovered by Napoleon’s army near the Rosetta
branch of the Nile in 1799.
 It is made up of 3 panels, each inscribed in a differeny
type of writing: Greek down the bottom third, demotic
script of Egyptian in the middle, and ancient
hieroglyphic in the broken upper third.
 It is now laid in the British Museum, where 4 plaster
cats were made for Oxford, Cambridge, Edinburgh and
Dublin Universities.

6. Jean Francois Champollion
 The greatest of all names associated to the study of
Egypt and the Rosetta stone.
 An Egyptologist.
 At 13, he was reading 3 languages, 17 he was appointed
to the faculty of the University of Grenoble. When he
was older, he had compiled a hieroglyphic vocabulary
and given a complete reading of the upper panel of the
Rosetta stone.
 He established correlations bet. Ind hieroglyphics and
greek letters (Ptolemy and Cleopatra)- cartouches –
”cartridge”.

7.  He formulated a system of grammar and general
decipherment that is the foundation on which all later
Egyptologists have worked.
 In general, the Rosetta stone had provided the key to
understanding one of the great civilization of the past.

8. The Egyptian Arithmetic
 E.A. was essentially additive, meaning that its
tendency was to reduce multiplication and division to
repeated additions.
 Multiplication of two numbers was accomplished by
successively doubling one of the numbers
(multiplier) and then adding the appropriate
duplication to form the product.

9. The Egyptian Arithmetic:
Multiplication
 Multiply 19 and 71.
1 71
2 142
4 284
8 568
16 1136
Total = 19

10. The Egyptian Arithmetic
 Multiply 19 and 71.
1 71
2 142
4 284
8 568
16 1136
Total = 19

11. The Egyptian Arithmetic
 Multiply 19 and 71.
 Multiply 23 and 40.
 Multiply 13 and 15.
 Multiply 23 and 88.
 Multiply 15 and 21.
 Multiply 8 and 49.
 Multiply 73 and 88.
 Multiply 113 and 140.

12. The unit fractions
 Unit fractions were the only ones recognized.
 But 2/3 was recognized with a special symbol .
 Doubling is not the only procedure; other numbers are
allowed in Egyptian Arithmetic: Division
 Decomposing fractions – fractions expressed as sum of
unit fractions ( fractions whose numerator is 1)

13. Decomposing fractions
 Rule: NO repetition of fractions
 Rewrite 6/7 as a sum of unit fractions.
1 7
½ 3.5
¼ 0.875
1/8 0.4375
1/7 1
1/14 0.5
1/28 0.25
1/56 0.125

14. Decomposing fractions
 Rule: NO repetition of fractions
 Rewrite 6/7 as a sum of unit fractions.
1 7
½ 3.5
¼ 0.875
1/8 0.4375
1/7 1
1/14 0.5
1/28 0.25
1/56 0.125
6

15. Decomposing fractions
 Rule: NO repetition of fractions
 Rewrite 6/7 as a sum of unit fractions.
 Check using your calculator if the result is correct!
1 7
½ 3.5
¼ 1.75
1/7 1
1/14 0.5
1/28 0.25
1/2+ ¼+ 1/14 + 1/28 6

16. Decompose the following
 3/5
 7/9
 5/8
 2/9
 3/8
 2/3
 2/7
 3/7
 3/4

17. Discovered Unit Fraction table
 The Rhind Papyrus- it contained a fraction table with 2
as the numerator and an odd number between 5 and
101 in the denominator.
 (e.g. 2/5, 2/7, 2/11, 2/13…)
 The general rule 2/3k = 1/2k + 1/6k; USE ONLY FOR
MULTIPLES OF 5
 Decompose 2/15
 1/10 + 1/30

18. Decompose the following using the
general rule
 2/10
 2/20
 2/25
 2/30

19. Additional Rules:
 Small denominators were preferred, with none greater
than 1000.
 The fewer the unit fractions, the better; and there were
never more than four.
 Denominators that were even were more desirable
than odd ones, esp. for the initial term
 A small first denominator might be increased if the
size of the others was thereby reduced.

20. Decompose the following
 2/5
 2/7
 2/11
 2/13
 2/17
 2/19
 2/23
 2/25

21. FRACTIONAL TABLE

22. Multiply the following with the aid
of the fraction table
 (2 + ¼) x (1 + ½ + 1/7)
1 1 + ½ + 1/7
2 2 + 1 + 2/7
½ ½ + 4 + 1/14
¼ ¼ + 1/8 + 1/28
Not a unit
fraction
(use table)

23. Multiply the following with the aid
of the fraction table
 (2 + ¼) x (1 + ½ + 1/7)
1 1 + ½ + 1/7
2 2 + 1 +1/4 + 1/28
½ ½ + 4 + 1/14
¼ ¼ + 1/8 + 1/28
2 + ¼ 2 +1 +1/4 + 1/28+ ¼ + 1/8 +
1/28
Or 3 + ½ + 1/8 +1/14

24. Multiply the following
 (11 + ½ + 1/8 ) (37)
 (1 + ½ + ¼) ( 9 + ½ + ¼)
 (2 + ¼) ( 1 + ½ + ¼)
 Show that the product of (1 + ½ + ¼) is equal to 1/8
 Show that the product of (1/32 + 1/224) and (1 + ½ + ¼)
is equal to 1/16

25. Divide 37 and ( 1 + 2/3 + ½ + 1/7)
1 1 + 2/3 + ½ + 1/7
2 2 + 1 + 1/3 + 1 + ¼ + 1/28 or
4 + 1/3 + ¼ + 1/28
4 8 + 2/3 +1/2 + 1/14
8 16 + 4/3 + 1 + 1/7 or
16 +1 + 1/3 + 1 + 1/7 or
18 + 1/3 + 1/7
16 36 + 2/3 + ¼ + 1/28

26.  2/3 + ¼ + 1/28 + ____ = 1
 2/3 + ¼ + 1/28 + x/84= 1
 x= 4; thus the fraction is 4/84 or 1/21
 So, y (1 + 2/3 + ½ + 1/7) = 1/21
 Y = 2/97 ( from the table = 1/56 + 1/67 + 1/776)

27. Divide 37 and ( 1 + 2/3 + ½ + 1/7)
1 1 + 2/3 + ½ + 1/7
2 2 + 1 + 1/3 + 1 + ¼ + 1/28 or
4 + 1/3 + ¼ + 1/28
4 8 + 2/3 +1/2 + 1/14
8 16 + 4/3 + 1 + 1/7 or
16 +1 + 1/3 + 1 + 1/7 or
18 + 1/3 + 1/7
16 36 + 2/3 + ¼ + 1/28
1/56 + 1/679 + 1/776 1/21

28. Representing rational numbers
 Two methods: Splitting method and Fibonacci’s
method
 Splitting Method: 1/n = 1/(n+1) + 1/ (n(n+1))
 1/9
 Where n = 9
 1/9 = 1/(10) + 1/(90)

29. Represent the following using
splitting method
 1/6
 2/5
 ¾
 5/7
 4/7

30. Leonardo of Pisa (Fibonacci)
 First step: find n1 satisfying 1/n1 ≤ a/b < 1/(n1-1)
 Then, a/b- 1/n1 = (n1a-b)/(bn1) = a1/b1
 Formula: a/b = 1/n1 + 1/n2 + … 1/nk + 1/bk
 Thus, a/b = 1/n1 + a1/b1

31. Fibonacci Method
 2/19
 Find n1 9< 19/2 <10; so 1/10 <2/19 <1/9
 Hence, n1 = 10; thus 1/n1 = 1/10
 Find a1/b1 2/19- 1/10 = (10x2-19)/(19x10) = 1/190
 So, 2/19 = 1/10 + 1/190

32. Express the fractions using
Fibonacci Method
 2/5
 1/6
 2/7
 ¾
 5/12
 4/9

33. Four Problems from the Rhind
Papyrus
 1. The Method of False Position
 -the oldest and most universal procedure for treating
linear equations
 -this method makes use of assumption of any
convenient value for the desired quantity, and by
performing the operations of the problem, to calculate
a number that can be compared with a given number.

34. Solve the linear equations by using
False Position Method
 Solve 8x/7 = 19
 Solution to be presented on the board.

35. Solve the value of x in the linear
equations using the false position
method
 2x/3 = 5
 3x/2=7
 5x/2=3
 4x/5=8
 5x/7=9

36. A number problem
 Think of a number, and add 2/3 of this number to
itself. From this sum, subtract 1/3 its value and say
what your answer is.
 For example, suppose the number is 10, then take away
1/10 of this 10…
 Then…
 the answer is 9. Thus, 9 is the first number thought of.
 WHY IS THIS SO? PROVE!

37. GAME:
 Create your own number problem. Be sure it is
working perfectly!
 Exchange with someone and be able to decipher the
answer.

38. Problem 79 in the Rhind Papyrus
 In each of seven houses there are seven cats; each cat
kills seven mice; each mouse would have eaten seven
sheaves of wheat; and each sheaf of wheat was capable
of yielding seven hekat measures of grain. How much
grain thereby saved?
 19607

39. Explanation
 Houses 7
 Cats 49
 Mice 343
 Sheaves 2,401
 Hekats 16,807
 19,607