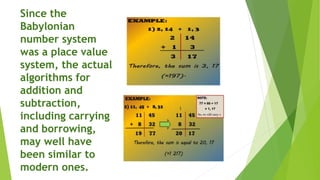
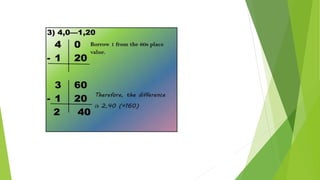
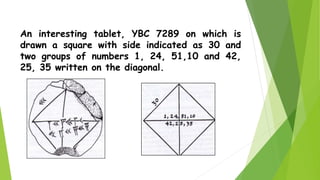
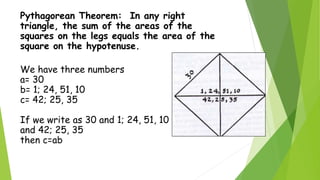
Ancient Mesopotamian mathematics was developed by scribes in Babylonia and Sumer in the 3rd millennium BC. They used a place-value number system with a base of 60 and performed calculations on clay tablets. Geometry problems involved finding areas and volumes by using coefficient lists of constants. The Mesopotamians could approximate square roots and knew the Pythagorean theorem, as evidenced on a tablet dated around 1900 BC. They could also solve basic equations, as shown by a problem on a tablet involving the yields of two fields.

1. HISTORY OF
MATHEMATICS
Mesopotamia

2. “In Mathematics you don’t understand things,
you just get used to them.”
by JOHN VON NEUMANN; a Hungarian-
born U.S. Mathematician
(1903-1957)
“As far as the laws of Mathematics refer to
reality, they are not certain, and as far as
they are certain, they do not refer to
reality.”
by ALBERT EINSTEIN; a German-born U.S.
Physicist
(1879-1955)

3. WHAT IS MATHEMATICS?
 It is the study of relationships among
quantities, magnitudes, and properties and
of logical operations by which unknown
quantities, magnitudes and properties may
be deduced.
 In the past, Mathematics was regarded as
the science of quantity, whether of
magnitude, as in geometry, or of numbers,
as in arithmetic, or of the generalization of
these two fields, as in algebra.

4. ANCIENT MATHEMATICS
The earliest records of advanced,
organized Mathematics date back to the
ancient Mesopotamian country of Babylonia
and to Egypt of the 3rd millennium BC.
There Mathematics was dominated by
arithmetic, with an emphasis on
measurement and calculation in geometry
with no trace of later mathematical
concepts such as axioms or proofs.

5. MATHEMATICSIN
MESOPOTAMIA

6. SHORT BACKGROUND ABOUT
MESOPOTAMIA
 The Mesopotamian civilization is perhaps a bit
older than the Egyptian, having developed in
the Tigris and Euphrates River valley beginning
sometime in the fifth millennium BCE.
 The dynasty of Ur produced a very centralized
bureaucratic state. In particular, it created a
large system of scribal schools to train members
of the bureaucracy. Although the Ur Dynasty
collapsed around 2000 BCE and was replaced by
the Hammurapi Dynasty.

7.  By 1700 BCE, the Hammurapi’s Dynasty expanded
his rule to much of Mesopotamia and instituted a
legal system to help regulate his empire.
 Writing began in Mesopotamia, quite possibly in
the southern city of Uruk, at about the same time
as in Egypt, namely, at the end of the fourth
millennium BCE. In fact, writing began there also
with the needs of accountancy, of the necessity of
recording and managing labor and flow of goods.
 In the temple of goddess Inana in Uruk, the
scribes represented numbers on small clay slabs,
using various pictograms to represent the objects
being counted or measured.

8. IMPORTANCE OF MATHEMATICS FOR THE
MESOPOTAMIANS (Why did the Mesopotamians
need Math?
To measure the
plots of their land
Taxation of
individuals
Development of
their lunar calendar

9. SUMER
It is considered as the
cradle of civilization
wherein Mathematics
was practiced by small
group of literate scribes
and when the earliest
writing system was
developed.

10. Ancient
Mesopotamian
Mathematics was
written with
stylus on clay
tablets.

11. METHOD OF
COMPUTATION
BABYLONIAN NUMBER
SYSTEM OR PLACE VALUE
SYSTEM

12. BABYLONIAN NUMBER SYSTEM (PLACE
VALUE SYSTEM)
 It is a sexagesimal number system
with a base of 60 number system.
(Note that the Mesopotamian
sexagesimal system does not have a
symbol zero nor a decimal point.
 On here, only two basic signs were
used-a vertical and a tilted stroke.

13. VERTICAL STYLUS STROKE
WHICH REPRESENTS 1
TILTED STROKE WHICH
REPRESENTS 10

14. EVALUATE THE PICTURE

15. FOR EXAMPLE:

16. Since the
Babylonian
number system
was a place value
system, the actual
algorithms for
addition and
subtraction,
including carrying
and borrowing,
may well have
been similar to
modern ones.

18. As the place value system was
based on 60, the multiplication
tables were extensive. Any given
one listed the multiples of a
particular number.

19. BABYLONIAN FRACTIONS
PLACE VALUE SYSTEM

20. RECIPROCALS
 If ab is equals
to 1, then a
and b are
reciprocals.
But in base-60,
1=0;60

21. DIVISION

22. GEOMETRY IN
MESOPOTAMIA

23. In general, in place of our
formulas for calculating such
quantities, the ancient
Mesopotamians made coefficient
lists, lists of constants that
embody mathematical
relationships between certain
aspects of various geometrical
figures.

24. EXAMPLE:
Thus, the number 0;52,30 (= 7/8) as the
coefficient for the height of a triangle
means that the altitude of an equilateral
triangle is 7/8 of the base, while the
number 0;26,15 (= 7/16) as the coefficient
for area means that the area of an
equilateral triangle is 7/16 times the square
of a side.

25.  On tablet BM 96954, there are several problems
involving a grain pile in the shape of a
rectangular pyramid with an elongated apex,
like a pitched roof. The method of solution
corresponds to the modern formula:
𝑙 – length of the solid
𝑤−width
ℎ− height
𝑡− length of the apex

26. SQUARE ROOTS AND
PYTHAGOREAN
THEOREM

27. YALE BABYLONIAN COLLECTION
(YBC) 7289

28. An interesting tablet, YBC 7289 on which is
drawn a square with side indicated as 30 and
two groups of numbers 1, 24, 51,10 and 42,
25, 35 written on the diagonal.

29. Square Roots:
YBC 7289 is a Babylonian clay tablet notable
for containing an accurate sexagesimal
approximation to the square root of 2, the
length of the diagonal of a unit square.
In particular case of √2 or √N , one begins
with a= 1;20 (=4/3). Then b= 0;13,20 and
1/a= 0;45. Take note: C can be choosen to
equal (1/2)b(1/a). The formula is √N= a +
(1/2)b(1/a) and the answer will be √2= 1;20 +
(0;30) (0;13,20) (0;45)= 1;20 + 0;05= 1;25.

30. FORMULA ;
√N = a + (1/2) b (1/a)
GIVEN ;
a = 1;20 + (=4/3) or (0;30)
b = 0;13,20
1/a = 0;45
√N = √2

31. Pythagorean Theorem: In any right
triangle, the sum of the areas of the
squares on the legs equals the area of the
square on the hypotenuse.
We have three numbers
a= 30
b= 1; 24, 51, 10
c= 42; 25, 35
If we write as 30 and 1; 24, 51, 10
and 42; 25, 35
then c=ab

32. “PLIMPTON 322”
GIVEN :
x = 8/5 = 1.6
1/x = 5/8 = 0.625
FORMULA :
a = x - 1/x ÷ 2
c = x + 1/x ÷ 2
FIND B :
b = √c² - a²
a = 8/5 - 5/8 ÷ 2
= 1.6 - 0.625 ÷ 2
= 0.975 ÷ 2
= 0.4875
= 4, 875
c = 8/5 + 5/8 ÷ 2
= 1.6 + 0.625 ÷ 2
= 2.225 ÷ 2
= 1.1125
= 11,125
a = 4, 875 ÷ 125 = 39
c = 11,125 ÷ 125 = 89
b = √c² - a²
b = √89² - 39²
b = √7,921 - 1,521
b = √6,400
b = 80

33. SOLVING
EQUATIONS

34. Here is an example from the Old Babylonian text VAT
8389: One of two fields yields 2/3sila per sar, the second
yields 1/2 sila per sar, where sila and sar are measures for
capacity and area, respectively. The yield of the first field
was 500 sila more than that of the second; the areas of
the two fields were together 1800 sar. How large is each
field? It is easy enough to translate the problem into a
system of two equations with x and y representing the
unknown.

35. Babylonian scribe have initial assumption x and y
is both equal to 900:
2/3 (900) -1/2 (900)=500
600 - 450 =500
150= 500(move the 150 to the others side)
500-150= 350
the scribe presumably
realized that every unit increase in the value of x
and consequent unit decrease in the value
of y gave an increase in the “function” (2/3)x −
(1/2)y by 2/3 + 1/2 = 7/6

37. For example, here a problem from
tablet YBC 4652: I found a stone but
did not weight it ; after I added one
seventh and one eleventh [ of the
total ] it weighted 1 mina ( = 60 gin)

38. THANK YOU FOR
LISTENING!